声场分析，几何声学方法、统计声学方法以及波动声学方法

2．1．1　声场分析

1）几何声学方法

我们把声波的传播途径用声线绘出，可以找出直达声和头几次反射声所可能出现的分布情况，或从改变界面的形状以控制这些反射声，这就是我们常称的几何图解法，它和几何光学的假设相类似，见图2－1，即入射声线与反射声线出现在同一平面内，入射角等于反射角。

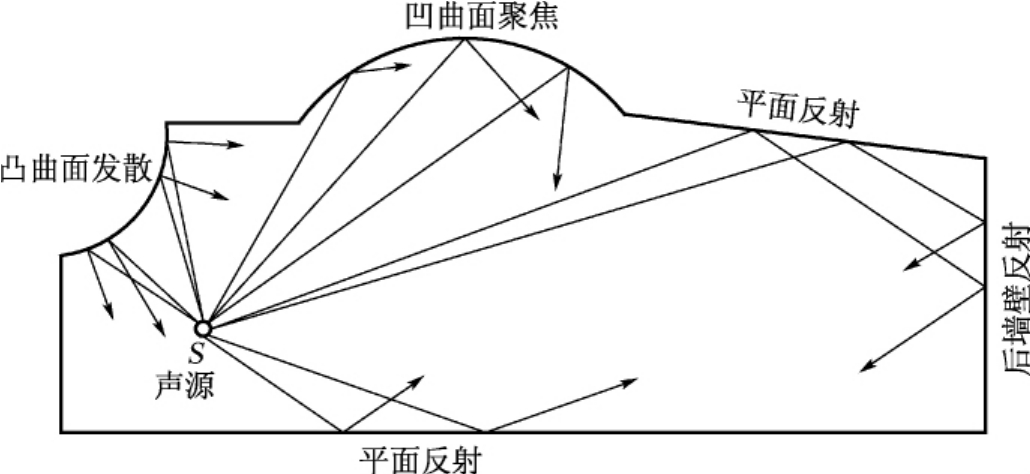
图2－1　声波传输途径声线图

几何声学只有在声波的波长比反射面尺寸小得多时才正确，但它可以使我们从房间的纵、剖面来了解声波在室内经过若干时间以后的反射情况，当然声波在壁面上反射多次以后，反射声线就已相当复杂和紊乱，甚至接近无规则分布了。

2）统计声学方法

当声源S在室内开始发声时，亦即当开始辐射声能时，这些形成的声波首先在室内自由传播，见图2－2。

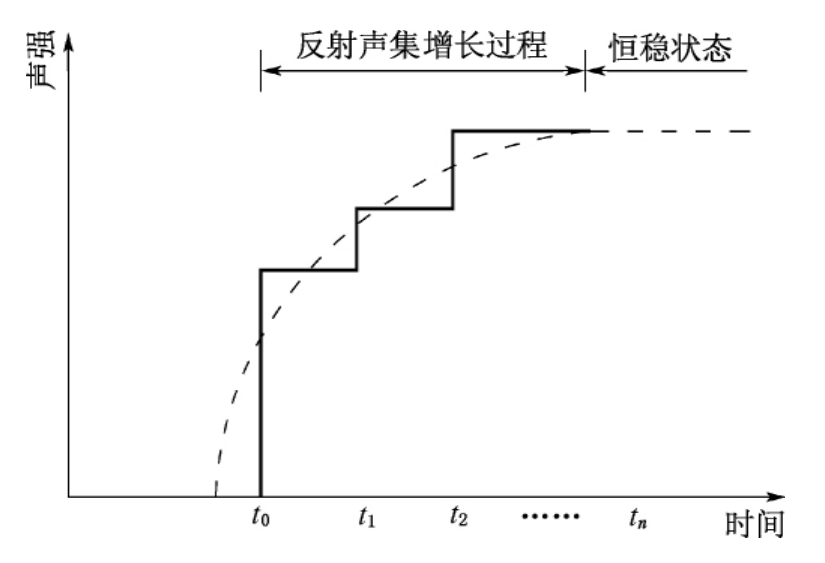
经过一定时间t后，首先有一直达声波O到达P点，P点的声强大小随SP的距离增大而减弱，时间t由SP的距离决定。在若干时间以后，又有由不同壁面反射而来的声波1、2、3……到达P点，它们的强度分别由不同壁面的吸收条件与SAP、SBP、SCP等的距离来决定，时间t₁、t₂、t₃等则分别为各该反射声到达P点所需的时间。如声源恒稳地继续发声，则各次反射波与入射波相继叠加起来，见图2－3。这种现象一直持续到一定时间t_n以后，P点的声强即逐渐到达恒稳状态，第n次反射到P点的声强已经很少而可以忽略不计了，于是室内声能不再增加，此时界面在每个单位时间吸收了和声源辐射相等的声能。

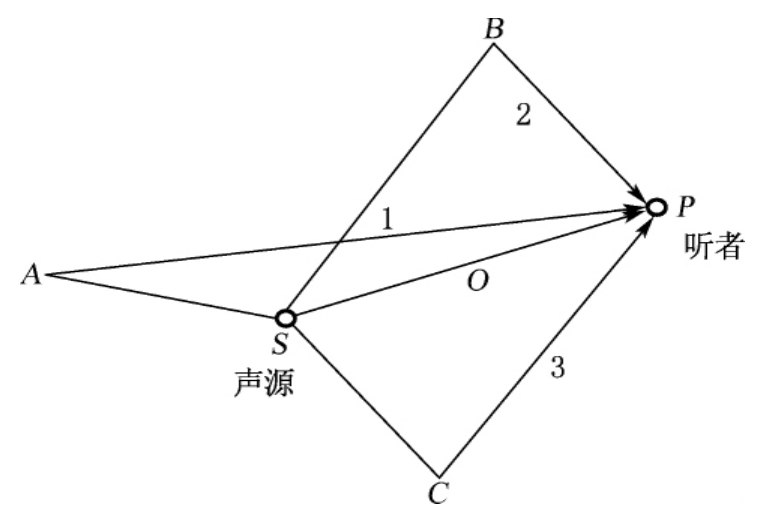
图2－2　室内声波辐射声能时的自由传播

(www.xing528.com)

图2－3　声源恒稳地继续发声时各次反射波和入射波的相继叠加

如室内表面的吸声效果差，则声音每次反射所损失的能量都很有限，反射波所集起的总声强就要比直达声波自己的强度高得多了，只要声源继续发声，该处总是保持这样高的强度，这一现象使我们更清楚地了解到某一时刻声源停止时，反射波并不能同时消失，而要继续在室内来回传播一定时间，以后每次受到反射时，每一个声波都因为吸收而失去一部分能量，室内的总声能就要渐渐减少，直到听不到为止。对听众来说，一个紧接一个的声波射至耳中，使它分辨不出是一个个的单能声音。因此在声源停止后，他听到的好像声音仍在延续，渐渐变弱直到听不到为止，所以光知道声射线的经历显然不够，而采用统计方法可以了解声射线的总体。

3）波动声学方法

几何声学和统计声学都没有考虑到声音的波动性质，而只是利用了声射线与反射的纯几何图形，然而声音现象的特征和重要的性质，尤其室内声学问题的仔细考虑，只有在波动理论基础上才能有全面而透彻的说明，也是我们向深层次研究室内声学的需要，问题是波动声学却包含了许多繁复的数学和物理概念，对于非专业工作者来说，并不是很熟悉，但在实际问题的处理过程中具有相当重要的原则性指导意义。本节略加叙述和介绍。

现在让我们重温一下几何声学和统计声学应用到室内的情况。一般包含有下列几个假设：①从声源发出的射线经过许多次连续反射以后即处于完全扩散的状态；②在声音的增强和衰减过程中仅考虑只有声源频率存在。但从实验中我们知道，声音在室内的增强与衰减除声源频率外，还有一些其他的频率存在，这些频率就是房间的共振频率，这些被激发的固有频率的迭加，必然引起声压有起伏很大的涨落，听音条件就有很大的不均匀性，而这些共振频率的分布均匀与否，与房间的尺度、比例和形状有着直接的关系：

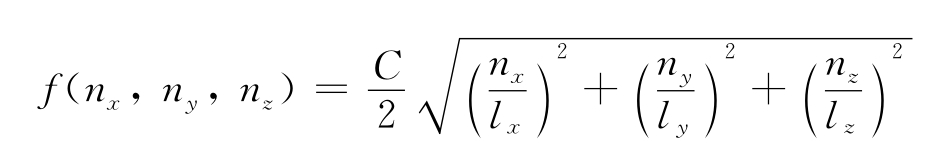
式中：f——各种可能的固有频率；

l_z、l_y、l_z——房间的几何尺度；

C——声音在空气中传播速度；

n_x、n_y、n_z——可分别选择从0→∞之间任何整数值。

从上式可以看出，波动声学使我们较清楚地了解房间内的简正振动方式，选择合适的房间尺度、比例和形状，可以减少或避免简正振动方式的简并，使本征频率分布均匀。

从上式还可以看出，房间的长（l_x）、宽（l_y）、高（l_z）三者比例若成整数倍，简正振动方式简并，本征频率分布不均匀，声学响应变得很不规则；声音在各频率的衰减有明显差别，在小房间和低频段尤为如此。所以我们在设计要求频率范围非常宽的播音室、录音室等用房时，波动声学的分析是很重要的。从分析中我们得出了房间三向尺度比例为2．4∶1．5∶1．0和3．2∶1．3∶1．0之间。

总之，实际工作中以统计声学分析为主，以几何声学分析为辅，再吸收波动声学中的一些有益的理论作为指导。