培养数学直觉思维，提高数学判断能力

二、直觉思维能力的培养

一个人的数学判断能力的高低主要取决于直觉思维能力的高低，徐利治教授指出：“数学直觉是可以后天培养的，实际上每个人的数学直觉也是不断提高的”，这也说明，数学直觉思维是可以通过训练提高的，如何培养学生的直觉思维能力呢？

1．让学生牢固掌握“双基”，这是培养学生直觉思维能力的前提

直觉的获得虽然具有偶然性和突发性，但绝不是无缘无故的凭空臆想，数学概念、法则、定理、由基本题型形成的知识块、解题的基本方法等基础知识的存在是产生直觉思维的前提；而且直觉思维能力的强弱与知识的积累的多少有关，知识储备越丰富越广泛，逻辑思维能力越强，学生的数学直觉思维能力就越强；有了广博的基础知识，才能广泛地联想，才能在不同知识领域获得借鉴，一个没有适当数学基础、没有较完善的认知结构的人，接触到新的数学问题，当然不可能作出应有的直觉判断；“没有苦思冥想，就不会有灵机一动，直觉的灵感是勤劳和自信的产物”。教师在教学中，必须高度重视“双基”的教学，不盲目的赶进度、不盲目的拔高教学要求，而是要针对学生的实际，在基础知识的“过手”上下工夫。例如，设P，Q为线段BC上两定点，且BP＝CQ，A为BC外一动点。当A运动到使∠BAP＝∠CAQ时，△ABC是什么三角形？试证明你的结论。在这道题中，根据已知条件”BP＝CQ，∠BAP＝∠CAQ”无法用三段论推知结论，必须用直觉来体会，凭直觉可猜得”AB＝AC”，即△ABC是等腰三角形。但是，只有对平面几何知识有较扎实的基础，才可能对问题的结论产生直觉。

2．鼓励猜想，这是培养学生直觉思维能力的关键

猜想是一种力图直接接触问题的本质，未必有充分根据的认识活动，因而猜想中所包含的成分与直觉思维是密切相关的。数学猜想（即使是错误的猜想）并不是毫无根据的胡思乱想，而是猜之有理、想之有据，是智慧的火花。

首先，教师在教学中要鼓励学生大胆猜想。教师要转变教学观念，把主动权还给学生，注意引导学生从整体上把握问题，鼓励学生大胆猜想，大步骤思维，不懈地要求学生归纳与演绎交互使用；教师应对学生的大胆猜想给予充分的肯定，即使出现错误也不能讥笑，而是让学生在愉快的氛围中大胆的猜想，小心地求证。

其次，教给学生猜想的方法。数学猜想是观察、实验、比较、归纳等思维活动的结果，同时又是思维活动的一种形式；可以通过观察、联想提出猜想，也可以通过归纳、类比提出猜想，还可以将问题一般化、特殊化提出猜想等。

3．重视解题教学，这是培养学生直觉思维能力的基础

数学教学当然离不开解题教学，教师要在教学中选择适当的题目来训练、培养学生的直觉思维能力；例如选择题，由于只要求从四个选择支中选出一个正确答案，省略解题过程，容许合理的猜想，有利于直觉思维的发展。实施开放性问题的教学，也是培养直觉思维的有效方法，开放性问题的条件或结论不够确定，可以从多角度由果寻因，由因索果，提出猜想，由于答案的发散性，有利于直觉思维的培养。

4．重视学生数学审美能力的培养，这是培养学生直觉思维能力的措施(www.xing528.com)

审美常常是在对对象的整体思考过程中得到的，因而审美对直觉思维有重要作用。数学美是一种理性的科学美，数学美中包含简单美、对称美、和谐美、奇异美等，对数学美的追求常常是数学创造的动力和源泉。例如（a＋b）²＝a ²+2ab+b ²，即使忘记了这个公式，也可以运用对称的观点判断结论的真伪。因此，在数学教学中，教师应充分揭示数学美，不断发现、创造数学美的素材，把自己发现、创造数学美的经验传授给学生，使学生不断提高对数学美的感受力、审美力，以激发学生对数学科学的兴趣爱好，以美启真，发挥审美的认识功能，提高学生的直觉思维能力。

5．重视在教学过程中培养学生的数学直觉思维， 这是培养学生直觉思维能的重点

法国科学院院士狄多涅认为:任何水平的数学教学的最终目的，无疑是使学生对他（她）要处理的数学对象有一个可靠的“直觉”。中学数学的教学不仅要使学生学会课本的知识、学会课本知识的严格表达，更要学会数学的精神、思想和方法，这就不仅仅是指逻辑推理。就数学创造而言，非逻辑的形象思维与直觉思维是绝对不可忽视的。

首先，在教学中要给学生留下直觉思维的空间。学生的思维能力是在实践和训练中发展的，在教学中适度推迟做出结论的时机，给学生一定的直觉思维的空间和时间，让学生做出直觉想象和判断，这是发展学生直觉思维能力的必要措施，讲解解例题时可以先让学生思考，也可以给学生留下少量的课后思考题，启迪学生的思维。

其次，注意教学的直观性。直观虽不等于直觉，但直观形象却有助于直觉思维的形成。数学教学中的直观性决不仅限于模型和画图，更重要的是应特别注意数学语言的直观性，表示丰富数学知识的语言——数学名词、术语、符号等都是抽象和简约的，每个数学命题都是由一些特定的语言组成的，要让学生不但熟悉这些语言、还应善于用通俗生动的语言阐述抽象难懂的原理，要善于比喻、借他山之石以攻玉，这样才有助与展开丰富的联想。

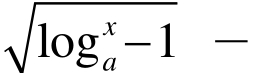
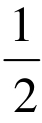
再次，提供丰富的背景材料，恰当地创设教学情景，促使学生整体思考。数学直觉思维的重要特征之一，就是思维形式的整体性。因此，着眼于从整体上揭示出事物的本质与内在联系，往往可以激发学生的直觉思维，从而导致思维的创新。例如，解关于x的不等式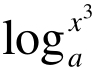：＋2＞0（其中a∈R），对此题做局部考察，用无理不等式、对数不等式的知识求解，将使运算量加大，容易出错，但从整体考虑，做换元: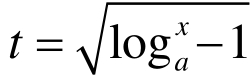，将使运算量大为减少，且减少出错的机率。

直觉思维与逻辑思维同等重要，偏离任何一方都会制约一个人的思维能力的发展，要以逻辑思维育直觉思维，以直觉思维促逻辑思维，开发学生内在的潜力，让学生的思维广度、深度、独立性、灵活性等方面全面得到发展。

【注释】

[1] 作者简介：四川省自贡市蜀光中学教师，四川自贡，邮编：643000