【摘要】：一般有换元法、化归法等，在此，仅以高考试题进行简单说明。以上是我们在高三复习教学中运用变式教学的一点设想和尝试。我们认为，数学练习的次数不能代替数学变式训练的强度。因此，在高三复习中组织变式练习，进行有效的变式教学是提高学生素质和数学素养的重要途径。
五、思维方式的变式
思考问题的角度发生改变，将问题转化为等价命题，从而利用熟悉的知识和方法解决具体问题。一般有换元法、化归法等，在此，仅以高考试题进行简单说明。
如有关恒成立问题转化为求函数的最值问题
已知函数f(x)=x 3+ax 2+bx+c在x=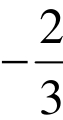
与x=1时取得最值.
(I)求a、b的值及函数f(x)的单调区间;
(II)若对x∈[−1,2]，不等式f(x)<c 2恒成立，求c的取值范围.
简析：(II)中，不等式f(x)＆lt;c 2恒成立，转化为求出函数f(x)的最大值是f(2)=2+c，(www.xing528.com)
最后解出c2＆gt+2+c，就是答案.c＆gt−1;c＆lt2;或
还有2006年重庆市(文)21题(3)问，2005年天津市(文)21题等都是要解决恒成立问题，也可以用同样的方法。
以上是我们在高三复习教学中运用变式教学的一点设想和尝试。我们认为，数学练习的次数不能代替数学变式训练的强度。前者仅重视量，后者的训练是具有思维挑战性的训练，是一种创造性的学习过程。因此，在高三复习中组织变式练习，进行有效的变式教学是提高学生素质和数学素养的重要途径。
【注释】
[1] 作者简介：西南交通大学附属中学教师，四川成都，邮编：610036
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
