三、高中生解题思维障碍的具体表现
1.数学解题思维的肤浅性
由于学生在学习数学的过程中,对一些数学概念或数学原理的发生、发展过程没有深刻地去理解,一般的学生仅仅停留在表象的概括水平上,不能脱离具体表象而形成抽象的概念,缺乏足够的抽象思维能力,学生往往善于处理一些直观的或熟悉的数学问题,而对那些不具体的、抽象的数学问题常常不能抓住其本质,转化为已知的数学模型或过程去分析解决。
例:已知实数x、y满足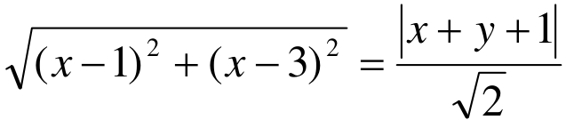 ,则点P(x , y)所对应的轨迹为( )
,则点P(x , y)所对应的轨迹为( )
(A)圆 (B)椭圆 (C)双曲线 (D)抛物线
在复习圆锥曲线时,我拿出这个问题后,学生一着手就简化方程,化简了半天还看不出结果就再找自己运算中的错误(怀疑自己算错),而不去仔细研究此式的结构,进而可以看出点P到点(1,3)及直线x+y+1=0的距离相等,从而其轨迹为抛物线。
2.数学解题思维定式的消极性(https://www.xing528.com)
学生运用掌握的知识,形成一套切实有效的分析解决问题的推理方式和方法,变成了学生的一种固定的思维模式,这种现象叫思维定式。但这种现象具有双重性,既有积极的作用,又有消极的作用。从正面说,思维定式的形成表明学生不仅掌握了知识,并且也形成了一定的思维推理能力;从反面说,这种思维定式对推理能力的发展和提高也具有一定的阻碍作用。在思维定式的作用下,往往自觉或不自觉地认为某种知识的应用范围是定向的,解决问题的方法是定型的。由于高中学生已经有相当丰富的解题经验,因此,有些学生往往对自己的某些想法深信不疑,很难使其放弃一些陈旧的解题经验,思维陷入僵化状态,不能根据新的问题的特点作出灵活的反应,常常阻抑更合理有效的思维甚至造成歪曲的认识。
例如:已知cos(α−β)= ,cosβ=
,cosβ=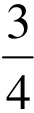 ,α>β,α,β均为锐角,求cosα。许多学生在刚学了两角和差的三角函数后做这道题,习惯性先把cos(α−β)=
,α>β,α,β均为锐角,求cosα。许多学生在刚学了两角和差的三角函数后做这道题,习惯性先把cos(α−β)=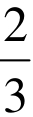 用差角公式展开,根据β为锐角算出sinβ,带cosβ,sinβ到展开式中,把sinα用
用差角公式展开,根据β为锐角算出sinβ,带cosβ,sinβ到展开式中,把sinα用 带换,从而转化为求解一个关于αcos的方程,然而此方程中含有根式,即使进行多次平方也不能解出αcos,但很多学生不愿放弃此方法,埋头苦算,因此走入了一个死胡同,其实仔细观察不难发现角的特点
带换,从而转化为求解一个关于αcos的方程,然而此方程中含有根式,即使进行多次平方也不能解出αcos,但很多学生不愿放弃此方法,埋头苦算,因此走入了一个死胡同,其实仔细观察不难发现角的特点
α=(α−β)+β,因此计算cosα也即计算cos[(α−β)+β],此时再用和角公式展开便不难发现只需再算出sin(α−β),sinβ既可,问题得以顺利解决。
3.数学解题思维的单向性
由于每个学生的数学基础不尽相同,其思维方式也各有特点,部分学生习惯性的单向思维也会给解题过程带来不同的思维障碍。
例如:计算tan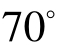 +tan
+tan −
−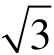 tan
tan ⋅tan
⋅tan 。此题考察了学生对正切和角公式的应用能力。实际上逆用公式
。此题考察了学生对正切和角公式的应用能力。实际上逆用公式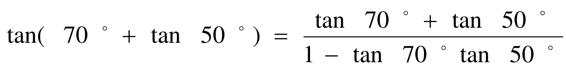 ,得tan
,得tan +tan
+tan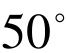 =tan(
=tan( +
+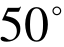 )(1−tan
)(1−tan ⋅tan
⋅tan ),问题便迎刃而解。
),问题便迎刃而解。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




