题目变换引申，创新思维更强。

三、反思题目能否变换引申

改变题目的条件，会导出什么新的结论，保留题目的条件，结论能否进一步加强，条件作类似的变换，结论能扩大到一般等等。像这样富有创造性的全方位思考，常常是学生发现新知识，认识新知识的突破口。

例如：在例5中：

变题1：将取值范围x∈ (0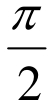，)，换成x∈（－，0）

则结论改为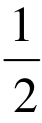：［f(x ₁)＋f(x ₂)］＜f()

变题2：若将函数tanx换成另外的函数，又可得到另一题。

例6：解不等式|x−7|−|x+3|＞8

分析：该题的一般解法是根据绝对值的意义，利用“零点”分段法，通过分成三段讨论去掉绝对值，这样解法思路清晰，明了，但有一定的运算量。若能从绝对值的几何意义考虑更能把握问题的实质。该不等式的几何意义为：在数轴上找一点，使得该点x到7和－3的距离之差大于8，易知不等式的解集为｛x|x＜－2｝(www.xing528.com)

类似地，可以给出如下变题：

（1）若不等式|x−7|+|x+3|＜a（a＞0）在实数集R上的解集是φ，求a的取值范围。

（2）若不等式|x−7|+|x+3|＞a（a＞0）对一切实数集x恒成立，求a的取值范围。

（3）若不等式|x−7|−|x+3|＜a（a＞0）的解集在R上不是φ，求a的取值范围。

（4）若不等式|x−7|−|x+3|＞a（a＞0）的解集在R上恒成立，求a的取值范围。

这组题与例6相比多了参数a，正是由于参数的引入，使学生的思维产生了障碍，这就要求学生对绝对值不等式的几何意义有清晰、深刻的理解。