数学反思：一题多解的思考方法

二、反思一题多解的方法

对一道数学题，往往是由于审题的角度不同得出多种解题方法，解完一道题后不能停留在所得出结论上，应引导学生再回过头来思考。教师向学生提出：你是怎么想的？为什么这样想？用发问的方式将学生的思维一步步展开，重现学生的思维过程并引导学生根据题目的基本特征，进行多角度观察、联想，找到更多的思维通道，去探索更好的解题途径。

证法1：（万能公式法）

设 tana＝t，则

证法2:1的变用

证法3：巧用倒数

依题意，sin2α≠－1

例5：（1994年高考题）

已知，函数f(x)＝tanx，x∈(0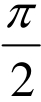，)，若x ₁，x ₂∈（0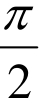，），且x ₁≠x ₂，

证法1：（综合法）

∴sin（x₁＋x₂）＞0 且 0＜cos（x₁－x₂）＜1

∴1＋cos（x₁＋x₂）＞cos（x₁－x ₂）＋cos（x₁＋x₂）

　　　　　　　　＝2cosx₁cosx₂＞0

证法2：(www.xing528.com)

在单位圆中作正切线AT₁＝tanx₁，AT₂＝tanx₂，不妨设0＜x₁＜x₂＜，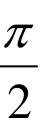

则|AT₁|＜|AT₂|，取T₁T₂的中点T_３，则AT_３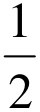＝(tanx₁+tanx₂)

作∠T₂0T₁的平分线交T₁T₂于T_４。

则AT_４＝tan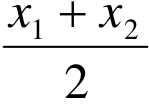

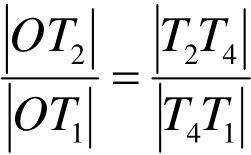∵，又|OT₂|＞|OT₁| ₂

∴|T₂T₄|＞|T₄T₁|，∴T₄在线段T₁T₃上

∴|AT₃|＞|AT₄|，AT₃与AT₄方向一致,

∴AT₃＞AT₄

即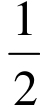(tanx ₁+tanx₂)＞tan()

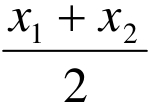故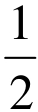[f(x ₁)+f(x ₂)]＞f()

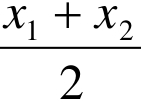除以上解法外，学生还会想到证明不等关系的其他方法，如：比较法中的比差法及比商法，均可以证明此题结论的成立。

这种思考其实就是“一题多解”，让学生从不同的角度去观察、分析、思考解题的方法，让学生进一步体会解题方法的多样性及灵活性，新旧知识的内在联系，使学生的思维空间更加广阔。