解题误区与反思：提高解题能力。

一、反思解题本身是否正确

由于在解题的过程中，可能会出现这样或那样的错误，因此在解完一道题后，就很有必要进行审查自己的解题是否混淆了概念，是否忽视了隐含条件，是否特殊代替一般，是否忽视特例，逻辑上是否有问题，运算是否正确，题目本身是否有误等。这样做是为了保证解题无误，这是解题后最基本的要求。教学中应有意识地选用一些错解或错题，进行解题后反思，使学生真正认识到解题后思考的重要性。

具有一双慧眼是每个人所希望的，能敏锐地观察出问题的细微之处，抓住问题的关键特征，而如若对这些细微之处视而不见，则会导致正确解法的“擦肩而过”。

例1：有一个棱长为a的正方体骨架，在其内部放置气球，对气球充气，使气球尽可能地膨胀成为一个圆球，则气球表面积最大值为（　 ）。

（A）πa²　（B）2πa²　（C）3πa²　（B）4πa²

错解　最大气球为正方体的内切球，由此可得到答案（A）。

反思　看题仔细吗？有无看错题或错解题意呢？事实上本题是“骨架”而不是封闭的正方体，因而最大的球应与正方体的各条棱相切，由此得答案（B）。

智者千虑，也有一失，在审题中，疏漏条件，思维不全，常常是很多同学的致命伤。

例2：已知sinθ、sin2x、cosθ成等差数列，sinθ、sinx、cosθ成等比数列，则cos2x的值为（　　）。

错解　 sinθ＋ cosθ＝2 sin2x，sinθ cosθ＝ sin² x，由此两式消去θ得

4 cosθ²2x－ cos2x－2＝0，

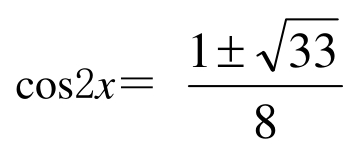，　　　　即选答案（C）(www.xing528.com)

反思　 一解还是两解？有无条件遗漏？事实上，sin² x＝ sinθ cosθ≤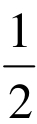，从而cos2x ≥0，故可排除答案（B）、（C）、（D），选（A）。

例3：求过点（0，2）的直线，使它与抛物线y ²＝4x仅有一个公共点。

错解　设所求直线　 y＝kx＋2

由　y＝kx＋2，

　　y ²＝4x.

得　 k² x ²＋(4k－4)x＋4＝0

令　Δ＝（4k－4）²－16k²＝0，

解得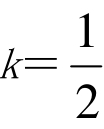　　　　

所求直线方程为．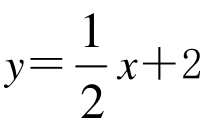

反思错误原因　 （1）认定所求直线的斜率一定存在；（2）忽视了“k＝0”的情况；（3）混淆了“相切”与“仅有一个公共点”这两个不同的概念。