高中数学知识网络化归纳：函数单调性概念复习

一、指导学生，归纳课本知识，构建高中数学知识的网络体系

数学学习，要理解知识产生的背景和形成的过程；要组成知识网络，使所学知识结构化、系统化。这样，才能避免“机械学习”；才能既习得“显性知识”，又习得“隐性知识”，所学知识才是完整的、全面的。因此，教师要指导学生，归纳课本知识，使知识结构化、网络化、系统化。

例如：函数单调性概念复习

函数单调性定义：如果对于属于定义域 I内的某区间的任意两个自变量的值 x₁，x₂当x₁＜x₂时，都有f（x₁）＜f（x₂）（f（x₁）＞f（x₂）），那么就说f（x）在这个区间上是增（减）函数。

（1）背景来源于初中所学的一次、二次、反比例函数的图像和性质，初中对单调性的定义是以图像形象地描述性说明，高中把图像特征加以抽象概括，以代数形式加以明确。

（2）“对于属于定义域I内的某个区间”说明函数的单调性仅是函数的局部性质，可能是整个定义域上的性质，也可能仅是定义域某个子区间性质。

（3）“属于定义域I区间的任意两个自变量的值x ₁，x ₂ ”特别强调“任意自变量”都须满足，不能有例外，这里有两层意义：第一，对某一点谈论函数单调性是无意义的。因此，单调区间是否包括端点值，主要由它的定义域决定，其余无妨。第二，只需x ₁，x ₂ 某一组取值构成反例即可否定单调性。

（4）具有理论上严谨地判定函数单调性的功能。有联系转化功能:揭示了单调区间上，自变量取值大小关系与相应函数值大小的互相联系转化的功能，有其一必有其二。还有形数结合功能：单调性对应图像变化趋势，对应图像上横、纵坐标变化趋势的联系。

（5）常用等价形式：在I上为增函数⇔对任意x₁，x₂∈I都有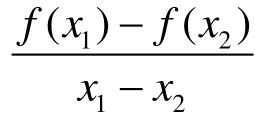＞0成立⇔在I上若f^/(x)存在，则f^/(x)≥0恒成立;

在I上为减函数⇔对任意x ₁，x₂∈I都有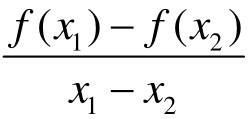＜0成立⇔在I上若f^/(x)存在，则f^/(x)≤0恒成立。

（6）常用函数的单调性：如一次函数、反比例函数、指数函数、对数函数、三角函数 、等差数列通项、前n项和对应的函数的单调性。

（7）与函数奇偶性一样是刻画函数自变量关系与函数值关系联系的重要性质，凡涉及勾通自变量不等关系与函数值不等关系的问题，均须注意函数单调性的意义 。(www.xing528.com)

（8）与函数单调性有关的命题：关于原点对称的区间上，奇函数有相同的单调性，偶函数有相反的单调性；f（x）反函数若存在，则原函数与反函数具有相同的单调性。

（9）函数单调性有关常用方法：

A．判定单调性方法

①定义法：任取值 → 做差→变形→ 定号→ 结论；

②导数法：求导→ 变形→定号→结论；

③图像法：作图→观察趋势→结论；

④复合函数法：设元→ 分解→判定基本函数→ 单调性→复合得结论；

⑤利用单调性等价形式判定法：如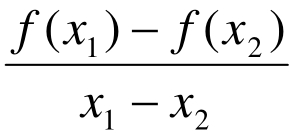的符号判定法。

B．单调区间求法：①定义法，②导数法，③图像法，④复合函数法。

（10）函数单调性的应用：①比较大小，②求最值，③求值域，④解方程，⑤解不等式，⑥证明不等式，⑦求参数范围，⑧求周期。