为了确定宝石矿物晶体的具体形态,必须确定晶面在空间的相对位置。
例如:同样是四方柱和四方双锥组成的聚形,而形态仍然不同,所以首先要进行晶体的定向(图2-7-1)。
一、晶体的定向及各晶系晶体常数特点
为了确定晶面在空间的相对位置,需将晶体置于选定的三维坐标系统中,根据晶面与坐标轴之间的关系,用符号表示出来。目前绝大多数宝石矿物的晶体结构已经确定,因此可直接利用宝石矿物晶体的晶格常数进行定向。
首先根据对称特点选择对称轴为晶轴,如无对称轴或对称轴数目不足时可选对称面的法线为晶轴;如果无对称轴,也无对称面时,则可选晶体上最发育的晶棱方向作晶轴。在等轴晶系、四方晶系、斜方晶系、单斜晶系、三斜晶系这5个晶系中,要选晶体的3个晶轴(X、Y、Z轴)。晶轴是交于晶体中心原点O的3条假想直线,使Z轴直立,原点以上为正(+),以下为负(-),左右方向为Y轴,原点之左为负,右为正,前后方向为X轴,原点之前为正(+),后为负(-),如图2-7-2所示。
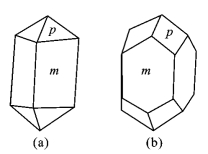
图2-7-1 四方柱与四方双锥组成的两种形态不同的聚形m.四方柱;p.四方双锥
晶轴之间的夹角称轴角,Y∧Z轴的夹角称α,Z∧X轴之夹角为β,X∧Y轴的夹角为γ。这样凡三轴晶体定向各晶轴之间的夹角为:等轴晶系α=β=γ=90°;四方晶系α=β=γ=90°;斜方晶系α=β=γ=90°;单斜晶系α=γ=90°,β≠90°,一般大于90°;三斜晶系α≠β≠γ≠90°。在三方及六方晶系定向时需选4个轴(X、Y、Z、U轴),仍使Z轴直立,晶轴相交于晶体中心,O为原点,原点以上为正(+),以下为负(-),X、Y、U三轴为水平,Y轴为左右方向,右为正,左为负,X轴为前后偏左方向,原点之前为正,后为负,U轴为前后偏右方向,前为负,后为正,如图2-7-3所示。这样在X、Y、U3个水平轴任何两个相邻晶轴的正端的夹角均为120°,α=β=90°,γ=120°。因此在晶体定向时必须按晶体对称选适当的晶轴,所选择的轴角α、β、γ必须尽量地等于或尽可能地接近90°。各晶系晶体常数特点如表2-7-1和图2-7-3。
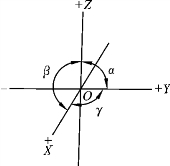
图2-7-2 3个晶轴方位
表2-7-1 各晶系晶体常数特点

续表2-7-1

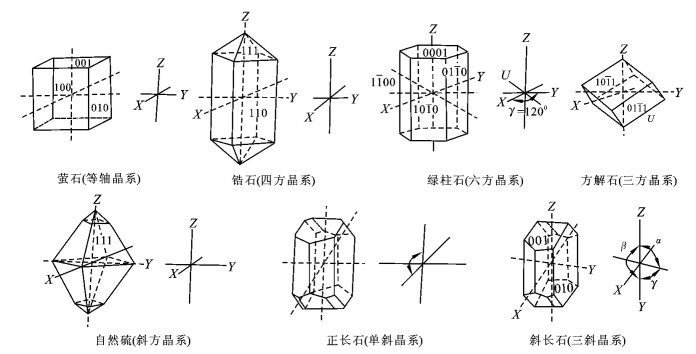
图2-7-3 各晶系晶体常数特征示意图
二、晶面符号、单形符号和晶带、晶棱符号
1.晶面符号
晶面符号,简称面号,是用晶面在3个晶轴上的截距系数的倒数比,用小括号括起来表示晶面相对位置。这种表示方法由1839年英国米勒(Miller W H)创立,所以称“米勒符号”。以图2-7-4为例,晶面ABC在3个晶轴的截距分别为OA=1a,OB=1b,OC=1c,其截距系数的倒数比为1/1∶1/1∶1/1=1∶1∶1,去掉比号,以小括号括起,即为(111),此即ABC晶面的米勒符号。又如图2-7-4中的ANM晶面,在3个晶轴上的截距分别为OA=1a,ON=4/3b,OM=2c,其倒数比为1/1∶1/(4/3)∶1/2,通分化简后得米勒符号为(432)。4、3、2称为ANM晶面在X、Y、Z轴上的晶面指数,米勒符号的一般式可写作(hkl),其晶面指数按X、Y、Z轴顺次排列。三方晶系和六方晶系的晶体,晶面符号的一般式为![]() ,其晶面指数按X、Y、U、Z顺序排列。
,其晶面指数按X、Y、U、Z顺序排列。
米勒符号中的晶面指数是截距系数的倒数比,故晶面在晶轴上的截距越大则晶面指数越小,当晶面与晶轴平行时其截距系数为无限大,晶面指数则为零。晶面交某晶轴的负端者在晶面指数上加一横“-”。如图2-7-6为萤石晶体,其对称型为3L44L36L29PC,属等轴晶系,立方体共有6个晶面,其各晶面的符号分别为:P1(100)、![]() 、P3(010)、
、P3(010)、![]() )、P5(001)、
)、P5(001)、![]() 。
。
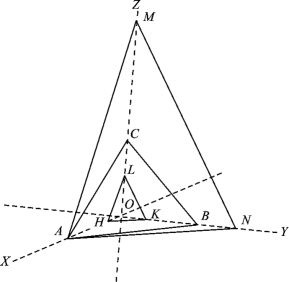
图2-7-4 晶面符号的图解

图2-7-5 三方和六方晶系3个水平轴的平面图(https://www.xing528.com)
2.单形符号
在一个单形上,一般是在晶体上符合前、右、上方的晶面的面号用大括号括起代表单形的符号,图2-7-6中的{100}、{111}即是单形符号。再以图2-7-6为例,四方双锥为{111}、四方柱为{100}皆是单形符号。
系统的定向确定晶面符号和聚形符号,可再以图2-7-7的锆石晶体为例。
(1)对称型:L44L25PC属四方晶系,中级晶族。
(2)分析单形:四方柱和四方双锥组成的聚形。
(3)选L4为Z轴,L2分别作为X、Y轴,使三轴互相垂直。
(4)定出晶面符号及聚形符号:①四方柱由4个晶面m1、m2、m3、m4组成,晶面m1在X、Y、Z轴上的截距分别为OD0、∞、∞(晶面与晶面平行其截距可视为在无限远处相交故用∞表示)则h∶k∶l=OA0/OD0∶OB0/∞∶OC0/∞=n∶0∶0=1∶0∶0,故m1的晶面符号为(100);同理可得m2为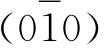 、m3为
、m3为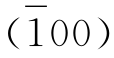 )、m4为(010),这当中符合“前右上”的晶面只有(100),它符合前无左右上下之分,故将(100)用大括号括起为{100},此即四方柱的单形符号。②四方双锥由8个晶面组成(P1、P2、P3、P4、P5、P6、P7、P8),P1晶面在X、Y、Z的截距为OA0、OB0、OC0,截距系数为OA0/a∶OB0/b∶OC0/c=1∶1∶1,取其倒数比仍为1∶1∶1,故P1面的面号为(111),同理得P2为
)、m4为(010),这当中符合“前右上”的晶面只有(100),它符合前无左右上下之分,故将(100)用大括号括起为{100},此即四方柱的单形符号。②四方双锥由8个晶面组成(P1、P2、P3、P4、P5、P6、P7、P8),P1晶面在X、Y、Z的截距为OA0、OB0、OC0,截距系数为OA0/a∶OB0/b∶OC0/c=1∶1∶1,取其倒数比仍为1∶1∶1,故P1面的面号为(111),同理得P2为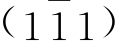 、P3
、P3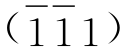 )、P4
)、P4 、P5
、P5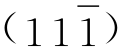 、P6
、P6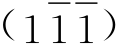 、P7
、P7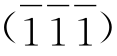 )、P8
)、P8 )。在这8个晶面中符合“前右上”的晶面为P1,所以P1晶面符号用大括号括起,{111}即为此四方双锥的单形符号。等轴晶系、四方晶系、斜方晶系、单斜晶系、三斜晶系的单形符号即是如此,而三方和六方晶系则不同。三方晶系及六方晶系因晶体的晶轴中分别有L3或L6(或
)。在这8个晶面中符合“前右上”的晶面为P1,所以P1晶面符号用大括号括起,{111}即为此四方双锥的单形符号。等轴晶系、四方晶系、斜方晶系、单斜晶系、三斜晶系的单形符号即是如此,而三方和六方晶系则不同。三方晶系及六方晶系因晶体的晶轴中分别有L3或L6(或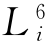 ),可以选它作为Z轴。以3个与Z轴垂直并在同一水平面上,而且彼此正端交角为120°的3L2或3P的法线(或符合上述条件的3个主要晶棱方向)分别作X、Y、U轴,在六方晶系晶体上使六方双锥、六方单锥、三方双锥3个单形的晶面成为单位面;在三方晶系晶体上除上述3种单形外,应使三方双锥、菱面体的晶面成为单位面,从而确定X、Y、U轴的位置。三方、六方晶系晶体定向举例见表2-7-1中举例的绿柱石和方解石即可。绿柱石的两种定向方法如图2-7-8,其中(a)方法较好。
),可以选它作为Z轴。以3个与Z轴垂直并在同一水平面上,而且彼此正端交角为120°的3L2或3P的法线(或符合上述条件的3个主要晶棱方向)分别作X、Y、U轴,在六方晶系晶体上使六方双锥、六方单锥、三方双锥3个单形的晶面成为单位面;在三方晶系晶体上除上述3种单形外,应使三方双锥、菱面体的晶面成为单位面,从而确定X、Y、U轴的位置。三方、六方晶系晶体定向举例见表2-7-1中举例的绿柱石和方解石即可。绿柱石的两种定向方法如图2-7-8,其中(a)方法较好。
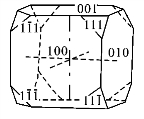
图2-7-6 萤石聚形
立方体{100}与八面体{111}相聚

图2-7-7 锆石晶体
p.四方双锥{111};m.四方柱{100}
3.晶带及晶带符号(晶棱符号)
晶体上的晶面都是呈带状分布的(图2-7-9),晶带是指交棱(包括晶面延展后相交的棱)互相平行的一组晶面的组合。如图2-7-9(b)中的(100)、(001)、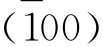 )及
)及 组成一个晶带,(010)、(001)、
组成一个晶带,(010)、(001)、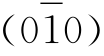 )及
)及 也组成一个晶带,(100)、(010)、
也组成一个晶带,(100)、(010)、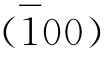 及
及 )则组成另一个晶带。图2-7-9(a)中晶体上共有6个晶带,图2-7-9(b)中晶体上共有9个晶带。通过晶体中心,并且平行晶带上交棱的方向线称晶带轴,如图2-7-9(c)中的CC′线即为晶面
)则组成另一个晶带。图2-7-9(a)中晶体上共有6个晶带,图2-7-9(b)中晶体上共有9个晶带。通过晶体中心,并且平行晶带上交棱的方向线称晶带轴,如图2-7-9(c)中的CC′线即为晶面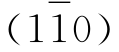 、(100)、(001)、
、(100)、(001)、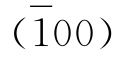
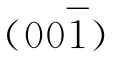 晶带的晶带轴。晶带的方向是以晶带轴的方向来表示,而晶带轴的方向又是用平行于该轴的晶棱方向来表示。
晶带的晶带轴。晶带的方向是以晶带轴的方向来表示,而晶带轴的方向又是用平行于该轴的晶棱方向来表示。
晶体上任何一个晶棱在空间的方向,都可以用一定的符号来表示。晶棱符号表示方法如下。
表示晶棱方向的符号,应该说是一条直线,它不牵扯晶棱的具体位置,即所有同一晶体上的平行晶棱具有同一个晶棱符号。其确定方法为:①将晶棱平移使之通过晶轴原点(O);②在其上任取一点求出此点在3个晶轴上的坐标(X、Y、Z);③以轴长来度量,即求出晶棱符号X/a∶Y/b∶Z/c=r∶s∶t;④去掉比例符号以中括号括之即[rst]。此即为该晶棱的晶棱符号。以图2-7-10为例,可以这样计算:设晶体上有一晶棱AB,先将其移至晶轴原点,在其上任取一点M,M点在这3个晶轴上的坐标分别为OH、OK、OL,以3个轴上的轴单位分别度量OH、OK、OL,则OH=2a、OK=4b、OL=6c,其中2、4、6分别为X、Y、Z轴上的坐标系数,最后取M点在这3个轴上的坐标系数之比为r∶s∶t即2∶4∶6,再化简为1∶2∶3,去掉比号,将1、2、3用[ ]括号括起,该AB晶棱的符号为[123]。
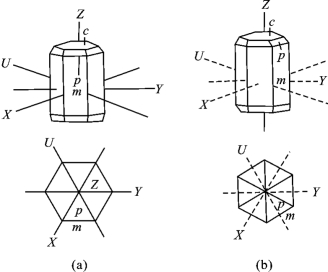
图2-7-8 绿柱石的两种定向方法
(a)将X、Y、U实线轴选在棱上,p ,m
,m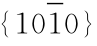 ,c.{0001};
,c.{0001};
(b)将X、Y、U虚线轴选在面上,p ,m
,m ,c.{0001}。
,c.{0001}。
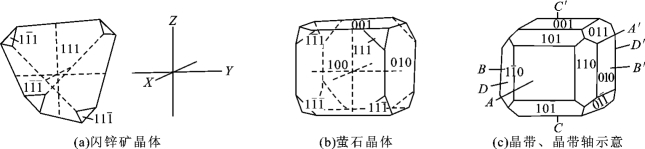
图2-7-9 晶面在晶体上呈带状分布
由此可以看出,在同一单形上晶面指数的绝对值是相同的,正负符号不同,这说明了不同晶面在空间的位置不同,如此看来,互相平行的晶棱,符号是相同的,即指数是相同的,正负符号是不同的,如[123]与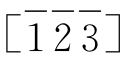 为同一方向晶棱。既然互相平行的晶棱符号相同,因而晶带的方向就可以用晶棱,也就是晶带轴的符号来表示。而且可看出平行X轴的晶棱符号为[100],平行Y轴的为[010],平行Z轴的为[001]。三方晶系、六方晶系为4个指数[rsvt],而且前3个指数的代数和为0,即r+s+v=0,平行Z轴的晶棱符号为[0001]。
为同一方向晶棱。既然互相平行的晶棱符号相同,因而晶带的方向就可以用晶棱,也就是晶带轴的符号来表示。而且可看出平行X轴的晶棱符号为[100],平行Y轴的为[010],平行Z轴的为[001]。三方晶系、六方晶系为4个指数[rsvt],而且前3个指数的代数和为0,即r+s+v=0,平行Z轴的晶棱符号为[0001]。
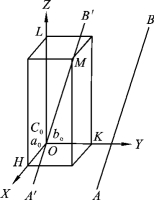
图2-7-10 晶棱符号的表示方法
这就达到了用符号给晶体定向,确定晶体具体形态的目的。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




