晶体的宏观对称及分类的分析介绍

一、对称的概念及晶体的对称

对称的现象在自然界是很常见的，对称的特点为：一是有相等部分，二是这些相等的部分作有规律的排列。如图2-5-1（a）和图2-5-1（b）所示。

图2-5-1（c）中只有相等部分而不作规律性的重复排列，故不能叫对称。

晶体的对称不仅表现在晶面、晶棱、角顶是作有规律重复排列，而且在晶体的物理性质（包括硬度、膨胀性、蚀像、折射率）、晶体结构、键性也表现出了对称。晶体的对称是晶体内部结构的外在表现，它也受晶体内部结构的控制。

图2-5-1　对称及不对称图形

二、对称操作及对称要素

为使晶体上相同部分重复出现，必须进行一定的操作，如旋转、反映等，为了进行对称操作又必须借助于一些假想的平面、直线或点，这些平面、直线或点称为“对称要素”。现将对称要素简述如下。

1.对称面（P）

对称操作是对平面的反映，是通过晶体中心的一个假想平面，它是垂直并平分晶面的平面，或垂直并平分晶棱的平面。对称面以P来表示。图2-5-2（a）中P1P1′平面是对称面。因为它可以把图形ABCD平均分成两个相等部分，这两个相等部分可互成镜像反映，P2P2′也同样是对称面。但在图2-5-2（b）中ADC平面就不是对称面。因为ADC平面和ABC平面不成镜像反映（只有AD′C平面才与ADC成镜像反映）。在一个晶体上可以没有对称面，也可有几个对称面。对称面的数目写在P的前面，例如在立方体上可有9个对称面，即表示为9P，如图2-5-3所示。

图2-5-2　对称面的概念示意图

2.对称轴（Ln）

对称操作是围绕一条直线的旋转。对称轴是一条通过晶体中心的假想的直线，晶体围绕此直线旋转一定的角度后，可使晶体相等部分以相同的位置重复出现或重合。晶体围绕此直线旋转360°后相等部分出现的次数谓轴次。使晶体上相等部分重复出现旋转的最小度数谓基转角“α”。晶体上n＝1、2、3、4、6，1次轴无意义，因旋转360°又复原是自然的。晶体上不可能出现L5，也不可能出现L7和大于L7的对称轴，这是因为L5、L7和＞L7的轴不能符合晶体内部格子构造原理。轴次n＞2的称高次轴，即L3、L4、L6都是高次轴。

图2-5-3　立方体上9个对称面分布的位置

晶体上存在对称轴的可能位置有：垂直晶面并通过晶体中心的直线如图2-5-4（a）所示；垂直并平分晶棱并通过晶体中心的直线，如图2-5-4（b）所示，这可能出现的位置只能是L2；还有通过角顶（角尖）并通过晶体中心的直线，如图2-5-4（c）所示。这3处可能位置是否就一定有该晶体的对称轴，还要具体分析。

有的晶体上可能没有对称轴，也可能同时有几个对称轴，同轴次的对称轴可将数目写在Ln之前，如果有几个轴可以按轴次由高到低顺序排列。图2-5-4（d）、图2-5-4（e）为绿柱石晶体，就有1个L6和6个L2；石英晶体就有1个L3和3个L2，如图2-5-4（f）所示；而萤石立方体晶体上则有3个L4、4个L3、6个L2，如图2-5-4（g）所示。

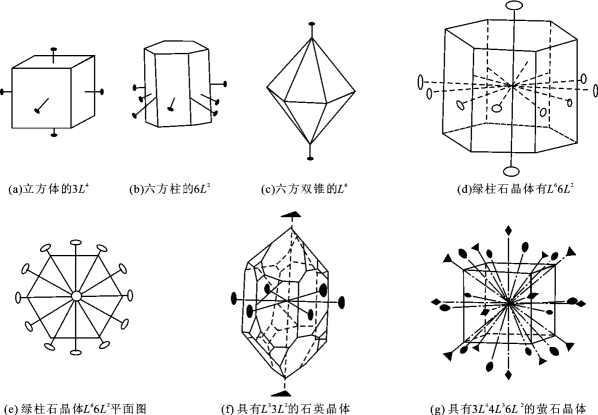
图2-5-4　晶体上的对称轴可能出现的位置

3.对称中心（C）

对称中心是晶体中的一个假想的几何点，在该点的相反方向等距离处有相等部分。相应的对称操作是对一点的反伸。

一个晶体只有一个对称中心，图2-5-5是具有对称中心C的晶体图形；有的晶体没有对称中心，图2-5-6是无对称中心的晶体图形。

图2-5-5　斜长石晶体对称型为C

(www.xing528.com)

图2-5-6　无对称中心的晶体

有对称中心则对称中心一定在晶体的几何中心，但是晶体的几何中心不一定都是对称中心。对称中心以C表示。有对称中心的晶体必然有相互平行、同形等大、而方向相反的成对晶面。

4.旋转反伸轴（）

相对应的对称操作是绕此轴转一定角度后再对轴中心点进行反伸的复合操作。此轴又称倒转轴，它是通过晶体中心的一条假想直线，晶体绕此直线旋转一定角度后再对此直线上的中心点进行反伸而使晶体上相等部分重复，如等。如图2-5-7和图2-5-8所示。这种轴在晶体上比较少见。

图2-5-7　反伸对称图

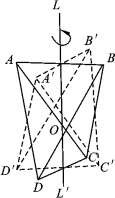
图2-5-8　四方四面体具有

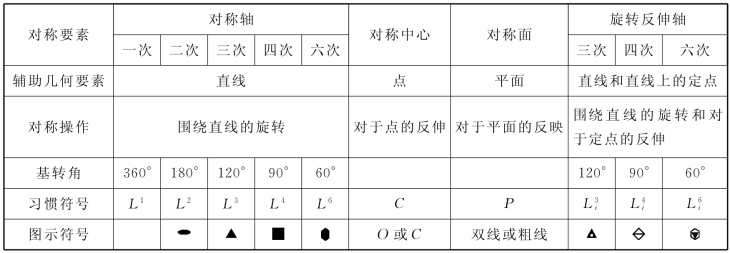
现将晶体上可能存在的宏观对称要素表列于表2-5-1中。

表2-5-1　晶体的宏观对称要素

三、对称型的概念

每种晶体的对称程度是不完全相同的，有的只有一个对称要素如斜长石晶体只能有一个C，又如金刚石的立方体、八面体晶体则有23个对称要素即3L44L36L29PC，把一个晶体上的这些全部对称要素按一定规律组合在一起的总合，则称对称型（又称点群）。

“点”是指进行对称操作时晶体上的中心点是不动的，也就是对称要素的交点。“群”是指数学上（群论）的概念，指可能推导出的全部不同的对称要素的组合。经过推导晶体上可能的对称要素组合只有32种，即平时所谓的32种对称型。其表示方法为先书写Ln，后写P，有C的话最后写C，其中又将轴次表示出由高到低顺序排列。如上所述对称型为3L44L36L29PC就是个很好的例子。晶体的32个对称型如表2-5-2所示。

表2-5-2　晶体的32种对称型

注：＊适用于n＝奇数；＊＊适用于n＝偶数。

四、晶体的分类

如果将对称型相同的晶体归为一类，即称为晶类。如金刚石、萤石、石榴石等宝石矿物，它们的晶体都可以呈立方体形状，也可呈八面体、菱形十二面体或更复杂的形态，但是它们晶体的对称型都是3L44L36L29PC，所以可以归为一个晶类。自然界有32个对称型，也就是有32个晶类。根据对称型中有无高次轴和高次轴的数目多少，又可将32个对称型分为高级、中级、低级3个晶族。然后再根据各晶族中各晶类的对称特点分为7个晶系，即等轴晶系、四方晶系、三方晶系、六方晶系、斜方晶系、单斜晶系、三斜晶系（表2-5-3）。

关于对称型符号在表2-5-3中列示了圣弗利斯符号和国际符号，在此不作讲述，僅仅参考。

表2-5-3　晶体的分类

续表2-5-3

注：对称型下有横线者为较常见的重要对称型。