供应链中的若干博弈问题介绍

供应链中的参与者（企业）以自身利益为基础的思考与供应链作为一个整体的最优性之间通常会发生冲突。成员之间的地位差异，产业链中的位置等因素都可能对其利益产生影响。虽然在供应链中的成员以独立决策为基础，但人们也非常关心在适当的博弃结构中能产生整体优化的某些效果。

例6.1.1 供应链协调问题

本例考虑一类较简单的供应链：由一个供应商与一个零售商组成的供应链，零售商以固定的价格P销售产品，这样需求与价格的关系就不在考虑之内，但促销的努力水平与需求有关。增加促销投入会扩大市场。那么、供应链中，由谁来作出促销努力呢？不同的供应链成员能否有足够的促销投入呢？

作为参考性的促销努力。下面把一体化情形的促销努力水平作为参考点，一体化是指零售商与生产商的决策由一个集中的决策中心制订，而供应商与零售商只是决策的执行者。先分析一体化促销努力水平。

设需求函数为

D（I）＝D0＋a Ib

其中I为促销投资，D0是不进行促销时的市场规模，D0＞0，其中a＞0，可以理解为促销投资的敏感性系数，b是投资的弹性。可以假定0＜b＜1，因为投资的边际效用递减。

假设单位产品的生产成本是C，销售价格是P，且P＞C，则一体化情况下利润由下式来给出最大化利润的促销投入

π（I）＝（P－C）（D0＋a Ib）－I

可令，即

（P－C）（ab I（b－1））－1＝0

可求得最优的促销投入为：

I＊＝［ab（P－C）］1／（1－b）

下面考虑的问题是，在一个分散决策的供应链中，制造商能否能过契约安排，促使零销售能以I＊作为最优的促销投入。

契约的主要决策变为两个：一个是制造商批发给零售商的批发价，记为W，按要求，C＜W＜P，（注：在考虑的背景中，C、P是不变的）。另一个是对零售商促销投资的补贴率S（0＜S＜1）。

这一契约下，焦点问题有两个，一个是利润的分享问题，虽然，不同的契约意味着不同的利润分配；另一个是能否激励零售商以I＊作为最优销售投入。

零售商的利润函数是：

令解得

在上式中，只要取S＊＝1－（P－W＊）（P－C），其中W＊是批发价，则有I＊2＝I＊，而相应的供应商利润π＊1与零售商利润π＊2之和是：

可以注意到W＊在C＜W＊＜P之间可以任意取，零售商利润π2

所以零售商的利润为正，但生产商可以提高批发价任意压缩零售商的利润。

上面的问题可以自然地拓广，讨论有多个零售商的问题，为此，分析有两个零售商的问题。

设I2、I3分别为两个零售商的促销投入，市场需求函数为

D（I2，I3）＝Do＋a（I2＋I3）b

该式假定，促销投入满足简单的加性关系，参数的定义同前。

当考虑多个零售商时，就产生了需求在零售商之间的分配问题，显然这是一个复杂问题。假设在I2＞0；I3＞0时，零售商按促销投入之比I1／（I2＋I3）与I2／（I2＋I3）获得市场份额，并且假定零售商不进行促销投资不是优化策略。

两个零售商获得同样的批发价与促销补贴的契约（W、S），因此，两个零售商的利润分别是：

请注意，这是一个动态博弈，先由供应商行动，确定（W、S），再在此基础上零售商之间进行同时确定促销投入的博弈，所以先分析在（W、S），给定的条件下，零售商之间博弈的均衡。

令得

即Do（P－W）I3＋a（P－W）（I2＋I3）b（b I2＋I3）－（1－S）（I2＋I2）3＝0同理，得

Do（P－W）I2＋a（P－W）（I2＋I3）b（I2＋b I3）－（1－S）（I2＋I2）3＝0

上述两式相减可得

Do（P－W）（I3－I2）＋a（P－W）（1－b）（I3－I2）（I2＋I3）b＝0

（I3－I2）（P－W）［Do＋a（1－b）（I2＋I3）］＝0

由于（P－W）≠0，（1－b）＞0，所以上式的解必要求I＊3＝I＊2，即最优投入相同。

再对上述两式相加，并由I2＋I3≠0的假设，得

a（b＋1）（P－W）（I2＋I3）b－2（1－S）（I2＋I3）＋Do（P－W）＝0

当I＊3＝I＊2时，上式在给定条件下有唯一解I¯＊＝I＊2＋I＊3。

可以解得，希望I¯＊＝I＊成立时，

注意到0＜S＊＜1的要求，若较少的W＊，可能S＊≤0，但较接近P的W＊可使0＜S＊＜1成立。这时供应链成立的利润总和等于一体化的利润。

同单一零售商一样，供应商可以提高W＊来压缩零售商的利润，但不能占得全部利润，与单一零售商不同的是，多个零售商的情况促使供应商提高批发价，因为S＊＞0提出的批发价要求更强化了供应商的地位。

该模型中的分析，利用了零售商之间市场分配的简单假设。实际的情况可能会更复杂。但也表明、适当的契约，供应链也可以达到一体化的效率。

例6.1.2 下游道德风险

零售商为消费者提供的服务，如送货，方便的退货会增加消费者效用。消费者更偏爱具有较高服务水平的产品，因而提高服务会扩大相关产品的需求。如果是一条一体化的供应链，相应的服务是整体利润最大化的一个决策变量。(www.xing528.com)

但在上下游关系中，供应商与零售商进行独立决策时，零售商是否会给消费者提供足够的服务？如果下游零售商因自身利益考虑不能提供足够的服务而使供应链的整体利润下降，这是道德风险。下面分析在线性价格下，服务不充分的道德风险是存在的。

设产品的单位成本是C，单位产品提供的服务水平记为S，S越大，表示服务水平越高，为提供S服务导致的成本是Φ（S）。以P的价格，S的服务为消费者供应产品时，需求可记为D（P、S），且满足。

纵向一体化时，由下式的最大化

T1＝［P－C－Φ（S）］D（P·S）

决定最优的价格及最优服务水平P＊、S＊。

可解得P＊、S＊。

在供应商以Pw的批发价向零售商批发产品时，供应商的利润是

π1＝（Pw－C）D（P·S）

零售商的利润是：

π2＝［P－Pw－Φ（S）］D（P·S）

在给定Pw时，零售商对上式求最优的P＊2、S＊2。

令及得

上式的解S＊2满足S＊2＜S＊。

这一问题表明，供应商需设计更复杂机制才能防治零售商的道德风险。

例6.1.3 显示产品质量的售后服务

在非供应链环境中，售后服务作为信号可用于向消费者显示产品质量的信息。

售后服务一方面给消费者带来效用，同时也是显示企业产品质量的信号。直观上，较高的售后服务水平如果没有相应的质量与之匹配，会导致太高的服务成本。下面分析该问题。

假设产品的质量不能在产品购买时直接检验，并且提高售后服务水平产生一个与产品质量相关的成本，为此，设想博弈的参与人是一家企业及一个消费者群体。

企业的产品质量有低、高二种类型，分别用θ＝1，2，来表示，企业承诺的服务水平用m来表示，m≥0，m的取值越大，表示服务水平越高。服务水平的成本一方面与质量有关，另一方面，同样的质量，提高服务水平会导致一个加速上升的成本，所以，假设与质量类型相关的提供的服务水平的成本为a（θ）mβ其中a（θ）＞0，且a （1）＞a（2），并且β＞1，这一成本设定表示低质量的产品导致较高的售后服务成本， β＞1显示边际服务成本上升。

为了集中分析售后服务问题，下面假设企业以固定价格销售产品，P是单位产品价格，C是单位产品成本，自然要求P＞C，若P价格下的市场需求是q，则企业的利润函数是：

π（θ，m，q）＝（P－C）q－a（θ）mβ

消费群体作为参与人，通过最优需求反应函数来设定博弈行为，其最优行为所产生的产品需求函数为：

q（θ，m）＝f（θ）（b＋mα） 0＜α≤1

其中f（θ）＞0，它是反应消费者的质量偏好的量，可假设f（1）＜f（2），（b＋mα）表示售后服务水平对需求的放大效应，所以b＞0。若α＝0，表示需求量与服务质量无关，这表明消费者并不认同售后服务作为反应质量水平的信号，所以基于分析的目的，可要求α＞0。同时，服务水平对市场规模扩大的边际效应是递减的，即0＜α≤1。

在此博弈背景中，企业的质量类型是企业的私人信息，企业以服务水平m为信号显示自己的类型，因此，该问题可以纳入信号博弈的框架内进行分析。

信号博弈的顺序如下，

1）自然确定企业类型，θ＝1，2，并且公布类型的分布登记处P¯（θ）＞0，P¯（1）＋¯P（2）＝1，企业知道自己的类型θ，消费者只知其分布。

2）企业向消费者发出m信号，消费者最优选择的需求函数q（θ，m）是公共知识。

3）消费者在接收到信号m后决定自己最优行动，结果是相应的需求函数。

下面分析这一博弈的均衡

首先分析分离均衡，若存在分离均衡、信号直接会显示企业的类型，则可以看到θ＝1型的最有效的信号m＊1＝0，因为π（1，m，q）＝（P－C）q－a（1）mβ1中，任何m1＞0都会带来损失，不如直接显示m＊＝0，即售后服务水平降到最底水平，而对θ＝2型的企业，既然信号可识别类型，m2≠0，但需要满足分离条件，即所选择的m＊2应满足：

1）（P－C）q（1）＜（P－C）q（2）－a（2）（m＊2）β

此式是指，θ＝2型混同于θ＝1型将导致损失。

2）（P－C）q（2）－a（1）（m＊2）β＜（P－C）q（1）

此式是指，θ＝1型混同于θ＝2型将导致损失，由此两式可得

（P－C）［q（2）－q（1）］／a（1）≤（m＊2）β≤［（P－C）［q（2）－q（1）］／a（2）］1／β

再分析混同均衡，假定两种类型的企业会选择同一个售后服务水平，则消费者按先验概率形成需求函数：

且要求

这是指θ＝1型不会直接用m＝0显示自己的类型，

因此对满足的信号。按直观标准，θ＝1型是不可能出此信号的。因此若具有信念P（2／m′＞m＊0）＝1，这时可以看到θ＝2型因选择更大的信号而扩大市场中获得大于混同时的收益，因为，当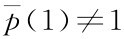时，对Δm充分少且大于0时，下式成立：（p－c）q（2）－a（2）（m＊2＋Δm）β＞（p－c）［p¯（1）q（1）＋p¯（2）q（2）］－a（2）（m＊0）β

因此，在直观标准下，该博弈唯一的均衡是分离均衡。

本例表明，售后服务水平可用于显示产品的质量。