不完全信息重复博弈的分析介绍

本节以一个基本博弈为基础，讨论重复博弈，前面已经讨论过重复博弈，是以完全信息为基础的，如我们可以回忆起，有限次囚犯困境重复博弈的唯一子博弈精炼纳什均衡是一次博弈纳什均衡的简单重复。完全信息重复博弈的有些结论让人怀疑，比如考虑连锁店悖论，明显觉得与实际的博弈不一致。人们直觉都认为重复囚犯困境博弈在开始阶段会合作，不至于每次都不合作。基于这些想法，研究工作转向了参与人类型上存在差异时的重复博弈，用不完全信息重复博弈来扩充简单的完全信息重复博弈的研究结论。

重复博弈的实验研究表明，当重复次数较多时，在博弈的开始阶段，合作是主流，这与大多数人的直觉是一致的，例如两个人进行1 000次囚犯困境博弈实验。我们都会预期前面的博弈会以合作为主，即使一个机会主义倾向严重的参与人，也会考虑到后面的博弈而在前n次博弈中选择合作。这实际上是通过前面的博弈行为，形成一种声誉，使对方相信你是一个可合作的对象，而在后面的博弈中把声誉兑换成收益。也就是说，博弈的前面各阶段冒被机会主义利用的危险而选合作是一种投资，指望在博弈的后续阶段得到回报，指望总收益增加。

把不完全信息整合到有限重复博弈中的一种方法是假设参与人有不同的类型，一类参与人是理性的，一类参与人是非理性的。理性的人会采取对策，而不理性者会采用一种固定的策略。重复囚犯困境的实验表明，不考虑对方特征，一种简单却优秀的策略是“一报还一报”策略，即首先选抵赖，后一次的选择与对方前一次的选择相同，这一策略简单、有效，且没有机会主义成分，因此可作为非理性人的策略。

下面以合作博弈为基础介绍不完全信息重复博弈的重要思想与内容再一次列出合作博弈的收益，如表（5.3）。

表5.3 合作博弈

该博弈进行一次时（不合作，不合作）是唯一的纳什均衡，为了后面讨论方便，用NC记不合作，C记合作。考虑以下面的方式扩张模型，参与人1有两种类型，类型R称为理性的，是指这类参与人并不排斥机会主义，只要有利可图，可以选择任何战略。类型Ⅰ称为非理性的，是指合作倾向重，并不首先选择不合作，只采用一种特殊的策略。假设Ⅰ型的参与人1选择一报还一报策略，而且不再考虑其他策略，参与人2只有理性一个类型。我们讨论的不完全信息重复博弈的顺序如下：

1）自然首先随机选择参与人1的类型。参与人1知道自己的类型，选择的概率分布是：理性人的概率为（1－p），非理性的概率为p。

2）两个参与人进行第一阶段博弈，同时选择行动。

3）公布第一阶段的行动后进行第二阶段的博弈。多次时如此延续。

4）参与人的支付是多阶段支付的总和。

这一博弈形式使我们可把分析目标集中在理性的参与人的行为。由于假设Ⅰ型的参与人只采用“一报还一报”策略，使得用博弈已经完成的历史比较容易判断出其类型。如一旦参与人1首先选择了NC，则就可肯定是理性的参与人，因为一报还一报永远不会首先选NC。我们希望的分析目标是R型参与人是否有选择合作的动机，即是否一开始就会选择NC。

先讨论博弈只重复二次的情况。

理性的参与人1，会在第二阶段选择NC，参与人2在第二阶段也会选择NC，因为第二阶段是最后阶段。而非理性的参与人1第一阶段选C，第二阶段将依据参与人2在第一阶段的选择而定。理性参与人1会在第一阶段的选择是NC，这是完全信息有限重复博弈时的结论，因为即使第一次选C，也不会影响参与人2的第二次选择。这样，参与人2第一次的选择给定时，据参与人1的类型，结果就已经给定了。若参与人1是R型的，则参与人2第一次选NC的总收益是1＋1＝2，选C时的收益是0＋1＝1。

若参与人1是Ⅰ型的，参与人2第一次选NC的总收益是5＋1＝6，选C的总收益是3＋5＝8，根据概率分布，参与人2第一次选NC，第二次选NC的总收益是1×（1－P）＋6P＝2＋4P，参与人2第一次选C，第二次选NC的总收益是1×（1－P）＋8P＝1＋7P，所以当1＋7P≥2＋4P，即P≥时，参与人2第一次选C第二次选NC是最优的，即参与人1属于非理性的概率不小于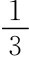时，参与人2第一阶段选C是最优的。

简单地说，即使博弈重复两次，当具有合作动机的参与人1的概率不小于时，有机会主义动机的参与人2也会在第一次博弈中选择合作，但重复二次时理性的参与人1却没有合作的动机。

现在再考虑博弈重复三次的情况。

理性的参与人1，第一阶段就选择NC可能并不是最优的，因为他选C时可以混同于非理性的参与人。

然而在倒数第二次博弈时，由于参与人2最后一次必选NC，再去混同又失去了意义。我们来证明：非理性参与人1采用一报还一报，理性参与人1第一次采用混同策略选C，以后二次就选NC。参与人2在第一阶段选C，若对手第一阶段选NC，则以后第二阶段、第三阶段都选NC，若对手类型无法区分，第二阶段选C，第三阶段选NC，这是一个精炼贝叶斯均衡，需要条件是P≥，这一策略组合下，理性参与人1三次的选择是C，NC，NC，非理性参与人1的选择是三次都是C，参与人2前两次是C，第三次是NC。实际上，在博弈的第三阶段，依据战略，理性的参与人1选NC，非理性的参与人1选C，参与人2选NC，有偏离条件的理性参与人1与参与人2都不会偏离，其它路径进入第三次，战略组合也给出了最优解。而在倒数第二次，理性的参与人1由于第一次时混同于非理性参与人1，分析同重复两次是一样的，其它路径进入第二阶段，战略组合的最优性可直接验证。第一阶段如果理性参与人1偏离为NC，则依据战略，参与人2将在第二，第三次选NC，理性参与人1偏离的收益是7，不偏离的收益是3＋5＋1＝9，所以不会偏离。而参与人2如果偏离为NC，则有两种情况：（NC，NC，NC）或（NC，C，NC）。

参与人2若偏向（NC，NC，NC）时，理性参与人1是（C，NC，NC），非理性参与人1是（C，NC，NC），其收益是（5＋1＋1）（1－P）＋（5＋1＋1）P＝7

参与人2若偏向（NC，C，NC）时，理性参与人1是（C，NC，NC），非理性参与人1是（C，NC，C），其收益是（5＋0＋1）（1－P）＋（5＋0＋5）P＝6＋4P

参与人2不偏离（C，C，NC）时收益是（3＋3＋5）P＋（3＋0＋1）（1－P）＝4＋7P。

在P≥时，4＋7P≥6＋4P，4＋7P≥7，因此参与人2不会偏离。

这就证明了只要非理性参与人1的概率大于，第一次就没有人会选不合作，即有机会主义倾向的参与人都主动选择了合作。

为什么三次重复时比两次重复时对P要求更高，博弈支付的设计是一个原因，若（NC，C）的策略组合收益是（4，0），可以检验，P可以更少。另一原因是参与人2利用了理性参与人混同而选NC导致了高收益，而后面二次的代价较低，再一个原因是最后一次的效应。

那么，博弈重复四次，合作的出现是否会要求比三次更大的P呢？或博弈次数越多越要求更大的P呢？实际上，可以换一个角度来思考。在多次重复博弈中，是否对任意P＞0出现不合作的次数是否会随P增加而增加呢？

只要重复的次数较多，非理性的参与人1是存在的，即P＞0，即使很小，我们可以看到在与非理性的参与人1博弈时，参与人2的收益是大的。可以证明，对手是一报还一报的参与人1时，参与人2的最优策略是一直选C直到最后一次才选NC。若不然，参与人2在非最后一次第一次选了NC，则（C，NC）与后面的（NC， x）的策略组合相连出现。参与人2这两次的收益是5＋f（x），f（x）可能是0。如果参与人2把（C，NC）中的NC改成C，那么下一阶段参与人1回报C，相邻之阶段的策略为（C，C），（C，x）。这样即使不涉及其他阶段的策略，而参与人2修改后的收益3＋g（x）是，g（x）可能是3，也可能是5。所以3＋g（x）≥6。因此参与人2把第一个NC改成C时收益不会下降。这样说明了参与人2应对非理性参与人1的最优策略是除最后一次选NC外，每次选C。在T＋1次与非理性参与人1的博弈中，收益是3（T＋5）。如果某一阶段选了NC，则下一阶段立即选C直到除最后一次才选NC是最优的。

参与人2与理性参与人1博弈时，理性参与人1如果主动选择NC，则选择NC之后的博弈，参与人2的最优策略是明显的。因为主动选择NC就直接识别了其理性类型。在接下来的博弈中，是二个理性参与人的有限重复博弈，最优策略是（NC，NC）重复出现，直到最后。所以理性参与人的最优策略是一旦选择NC，以后就是NC。因而纳什均衡是（C，C，…，C，NC，…，NC）这种前面合作后面不合作的结构。但合作次数可能为零，而非合作次数不可能为0。

基于上面的分析，合作的可能性就是要证明对于任意P＞0，如果博弈重复T＋1次，理性参与人第一阶段就选NC不是最优策略即可。

若理性参与人1第一阶段就选NC，由于在第二阶段就揭示了类型，第二阶段后二人将重复（NC，NC）不论第一阶段参与人2选什么，理性参与人1的最大收益是T＋5，最小收益是T＋1。

对参与人2，第一阶段就选NC只是为了防范理性参与人第一阶段就选NC是最优的。下面来考虑参与人2一直选NC是最优的条件。如果参与人2一直选NC是最优的，则理性参与人1一直选NC也是最优的，则参与人2的收益是（T＋1）（1－P）＋TP＋5。参与人2一直选NC为最优时，我们来考虑参与人2的另一种策略：如果参与人1不首先选NC，就不选NC，一旦参与人1主动选了NC，则就不再选C。这种策略下（实际上是冷酷战略），参与人1不偏离时，参与人2的收益是：碰到理性人，收益为T，碰到非理性人，收益为3（T＋1）。因此期望收益是T（1－P）＋3（T＋1）P，所以参与人2一直选NC为最优时要求其收益大于冷酷战略的收益，即（T＋1）（1－P）＋TP＋5≥T（1－P）＋3（T＋1）P，即2TP＋4P≤6或。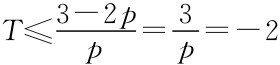

记，即T0是大于的最小整数，则当T＞T0时，一直选NC不是参与人2的最优策略。从证明过程可以看出，参与人2在T－T0之前主动选C比一直选NC更优。可以证明，纳什均衡必有这样的特征。在T－T0之前参与人都不会主动选NC，非理性参与人的一报还一报本身具有这一特征。而理性参与人主动选NC越早，由于身份认清后参与人2只能每次选NC，若在T1＜T－T0时暴露，则收益至少减少2（T－T0）－2。若参与人2在T－T0之前主动采用NC，依赖于理性参与人的反应，如果理性参与人象非理性参与人一样行动（也不会主动出NC）每选一次NC，收益至少减少1。总的可以概括为在T－T0之前，参与人选择一报还一报是均衡。对我们的分析目的而言，T－T0之后怎么样并不重要，因为合作已经出现了。如果参与人2也有理性与非理性类型，论述过程是一样的，而且可以相信，合作出现的时间将更长。

实际上，博弈次数较多时，在一定的时间内，理性的参与人把自己混同为非理性的参与人，而参与人2接受这种混同是最优的。可以注意到T0与p的关系，p越大，T0越小，而且T0与T无关，只与p有关。即从开始到T－T0阶段的合作可预期，只有一个确定的次数会出现不合作的局面，举例而言，如果T0＝10，则重复50次有最后10次的不合作，重复100次也只有最后10次不合作。

一般地，我们有如下的定理：

定理5.8.1 在T阶段重复合作博弈中，如果参与人中都有p＞0的概率是非理性的类型（他“采用一报还一报”策略），则存在一个T0，当T＞T0时，在T个阶段的重复博弈中，存在这样的精炼贝叶斯均衡策略路径，在开始到T－T0的阶段，观察到参与人都选择合作，而可能的不合作阶段的数量T0只与p有关，与T无关。

可以进一步说明的是，在T0之后的阶段，实际上不会有合作了。从前面的分析可以看出，参与人2此后每次选不合作最优的条件成立了，实际上是从一报还一报得来的收益不如理性的机会主义下的损失更大，忽略合作是最优的。

该定理与一般的直觉相同，它能使许多人从对完全信息重复博弈结论的疑惑中解脱出来。这里发生的一个突变要注意，p＝0时，完全信息重复博弈的结论是无论T多大都不会有合作，而p＞0就发生了质变，而且只要一方有非理性的参与人，则理性的参与人1，即使知道对方是毫无合作精神的，也会导致合作的局面。大概可以理解为合作本身是好的，因为防范机会主义而导致不合作，产生了很多的防范成本。只要有合作的理由，这个理由不太充分又何必太较真呢？

下面我们来分析政府的货币政策问题：

前面我们分析过政府的政策存在不一致性的问题，即承诺的政策具有不可置信的特征，但如果是多阶段的重复博弈，政府可能为了声誉，在一开始的阶段会遵守承诺。下面我们用模型来说明政府积累声誉的问题。

考虑有限期的政府与公众之间在通货膨胀政策上的博弈。因为一届政府可能经历有限个阶段的货币政策调整期。假设政府有两种类型：强政府与弱政府。强政府不采用通货膨胀政策，弱政府可能会偏向某些利益集团而选择通货膨胀政策。通过利益集团的满意来提高自己的效用。公众不知道政府的类型，只有在博弈开始时有一个强政府可能性的概率p0。单阶段博弈的规则如下：公众预期政府的通货膨胀率πe，政府可以观察到πe，进而选择实际的通货膨胀率，（单阶段内是一个动态博弈，公众预期在前，政府行动在后）。多阶段重复博弈是公众可以利用博弈已经历的阶段，来预期本期的通货膨胀率。

如果博弈只有两个阶段，这就是一个信号博弈。政府第一阶段的通货膨胀率是信号，以此信号影响公众第二期的预期。很显然，第一阶段不采用通货膨胀，第二阶段再来获取通货膨胀的收益可能会是弱政府的最优选择，即采用混同信号可能是均衡。

假设政府单阶段效用函数是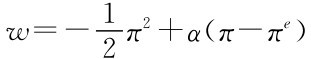：，其中π是政府的通货膨胀率，πe是公众对本期通胀的预期，α是政府类型的描述参数，α＝0表示强政府，意味着零通涨是强政府的最优选择。α＝1表示弱政府，这表明弱政府选择高于公众预期的通涨会增加效用。

假设公众的效用函数是：U＝－（π－πe）2，即公众在正确预期时获得最大效用。

下面先分析一个阶段的博弈均衡。

就单一阶段而言，给定公众预期πe的条件下，政府的最优通涨由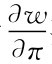决定，可得－π＋α＝0，即政府的最优反应是π＊（πe）＝α。公众的预期面临着政府类型的不确定性，与政府是强政府的初始信念p0有关。如果公众预期πe＝1，则收益是U（πe＝1，π＊（πe））＝－（1－1）2（1－p0）－（0－1）2p0＝－p0。如果公众的预期πe＝0，则收益是U（πe＝0，π＊（πe））＝－（1－0）2（1－p0）＝－（1－p0），所以当－p0＞－（1－p0），即p0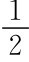＜时，公众的最优预期πe＝1。p0＞时最优预期是πe＝0。下面分析多阶段的博弈均衡。

当p0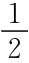＜时，由于弱政府一旦选择了π≠0，就意味着P（α＝1｜π≠0）＝1，如果在t时，弱政府选择π＊t是最优的，则以后每次选择也是最优的。假如弱政府t0时首次选择π＊t0＝1是最优的，若t0≠1，我们可以考虑t0－1阶段之后的博弈。在t0－1之前，由于弱政府选择了π＝0，在t0－1阶段公众选择是什么呢？由于没有调整信念的信息，而在t0之后的情况已定，公众在t0－1阶段的选择等效于一次博弈。因此，公众的。因此，弱政府t0－1阶段选πt0－1＝1，比选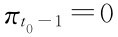能增加收益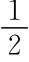，所以t0≠＝1时不可能构成均衡。事实上，当p0＜时，公众每一次预期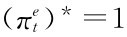，弱政府每一次选π＊t＝1强政府每一次选π＊t＝0。公众对强政府的信念是当π＊1＝0时，pi＝1，否则pi＝0。实际上，这是一个分离堆，强政府与弱政府不会选相同的信号。

若p0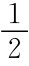＞，由于没有信号修正信念时，公众的最优预期是πe＝0，同样，弱政府在某一阶段t选择了π＊t＝0是最优时，之前必选π＊＝0，可以证明，弱政府不是最后一阶段选π＊t＝1都将导致损失。因为t之前的混同，使π＊＝0，（πe）＊＝0，所以没有揭示类型前的收益是0，而在揭示类型时的收益是，之后每一阶段收益是，t时揭示类型的收益是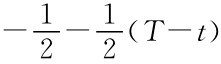，所以t＝T时收益最大，即直到最后一阶段才会显示类型，这就表明

弱政府

强政府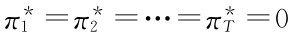

公众

后验信念p0＝p1＝p2＝…＝p T。这是一个子博弈精炼均衡，实际上是混同均衡。p0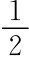＝时，弱政府在任何阶段揭示类型都无所谓。

这表明，在强政府的初始信念较高时弱政府在最后一个阶段之前会维持信誉。不会选择π＊＝1，只有到最后一个阶段，才会兑现信誉，将其转化为收益。这使得宏观政策的不一致性在声誉因素下可以获得解决。

第五章 习题

1.博弈树如图：(www.xing528.com)

1）是否有充足的理由说明参与人2不会选R；

2）参与人1选D，参与人2选D使博弈结束是均衡路径，求参与人3信息集的信念；

3）若信念体系符合消去劣战略的要求，求精炼贝叶斯均衡。

2.博弈树如图：

1）求它的纳什均衡；

2）参与人1选A结束博弈的均衡用什么原则可消去；

3）参与人1选A结束是子博弈精炼纳什均衡吗？

4）证明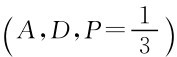序贯均衡；

5）证明参与人1选A结束是颤抖手均衡。

3.博弈树如图：

1）若参与人2选择的四个决策结属于同一个信息集，代表什么博弈？

2）证明该博弈上只有分离均衡。

4.分析下面信号博弈的均衡：

5.Q1服从均匀分布，是参与人1的类型，参与人1的信号是x，参与人2的策略是y，效用为U1（x，y，θ）＝（θ－x－y）x

U2（x，y，θ）＝－（x－2y）2

证明：该博弈上有分离均衡，并求出均衡。

6.下面（a）、（b）分别表示两个博弈：

1）把（a）、（b）都写成策略式表达；

2）证明（b）中参与人1选A结束博弈的均衡是颤抖手均衡；

3）证明（a）中选A结束博弈不是子博弈精炼纳什均衡；

4）分析（a）、（b）中对选A结束博弈时，参与人1的颤抖的差别。

7.一个班级内有2／3的同学20岁，1／3的同学19岁，在该班中等概率抽取一名同学作为参与人1，另一人为参与人2，要求参与人1报出自己的年龄（可以说假话），要求参与人2猜参与人1的真实年龄，收益如下：

分析该博弈的均衡。

第五章 参考答案与提示

1.1）R是参与人2的劣战略，参与人2不会选R理由充分；

2）p≥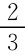

3）若用消去劣战略建立信念，参与人2选R概率为0。（D，L）是子博弈精炼纳什均衡的路径，此时p＝0。

2.1）参与人1选A结束博弈是纳什均衡，（C，U）是纳什均衡。

2）直观标准，选D的最大收益是1，不如选A的收益2。

3）是。该博弈没有非平凡的子博弈。

4）参与人1的策略是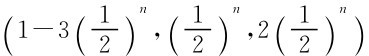，参与人2的策略为 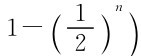，这时p＝，n→∞时即得结论。

5）参与人1选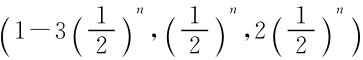，参与人2选

参与人1选A的收益是2，

参与人1选（1－ε1－ε2，ε1，ε2）的收益是

参与人2选D的收益是，

参与人2选（ε3，1－ε3）的收益是，

所以（A，D）是颤抖手均衡。

3.1）代表二人同时选择的不完全信息静态博弈；

2）A型选L是上策，B型选R是上策。

4.首先分析没有分离均衡，A型选R是上策，B型选T若为分离信号，则参与人2见R选U，见T选D，这时A型会选T。同样分析A型选L，B型选R也不是分离信号。

不同的P会混同不同的信号。

如果混同于T，参与人2的最优策略不可能是D，因为B型参与人的收益为0，而偏向R时的最少收益是1，混同于T时必然要求参与人2选U，参与人2取U的收益是2p＋（1－p），选D的收益是2（1－p），p≥。即参与人1选T，参与人2选U在p≥时，是混同均衡，若出现R被判为A型。同理，参与人1选R，参与人2选D在p≤时是混同均衡，若出现T被判为B型。注意在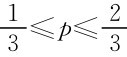时，可以在任一信号上混同，参与人2在任何情况下选U就只能混同于T，参与人2在情况下选D就只能混同于R。

5.y＊（x）＝是参与人2的最优策略；

6.1）两个博弈的策略式表达相同

2）分析同本章习题2

3）参与人1选D后的博弈是子博弈，参与人1选C是上策，（C，C）是该子博弈唯一均衡，因此参与人1第一次选D优于A；

4）在（a）中，参与人1偏向B的概率很小时，意味着选C的概率很大，在（b）中，参与人2的信息集中不能保证右边决策结的概率在1附近，就其颤抖而言，（a）更符合实际。

7.先画出博弈树，再分析。

参与人1都报20，参与人2猜20是混同均衡，

参与人1报真实年龄，参与人2报什么猜什么是分离均衡。

请比较第四章的习题3。