信号博弈的应用与例子的介绍

例5.6.1 本例是米尔格罗姆—罗伯茨垄断限价模型，是（5.3.1）市场进入例子更一般化的讨论。

垄断限价模型对现实经济中观察到的一个现象进行了有效解释。一般的垄断定价是指以垄断企业获得垄断利润的定价。而现实的垄断企业往往会低于垄断定价。为什么要降低定价？该模型用信号博弈来分析。模型表明垄断企业的价格是一种信号，用来表明自己的成本类型，使进入者在价格信号下不进入，从而维持长期的垄断。

假设有两家企业，企业1是在位者，企业2是进入者。考虑建立两个阶段的模型，在第一阶段，企业1是垄断者，选择价格P1；企业2可以观察到企业1在第一阶段的价格，在第二阶段可选择进入，进入后与企业1进行库诺特竞争。也可以选择不进入，企业2不进入时，第二阶段企业1仍然是垄断者，实际上假定企业2的进入决策是在第一阶段结束后瞬间完成的。

企业1的成本情况是私人信息，假定有高成本（用H表示）与低成本（用L表示）两种类型，用α（H）＝α，α（L）＝1－α分别表示在位者高成本与低成本的概率。如果企业1在第一阶段选择价格P1，两种类型企业在垄断的第一阶段利润分别为MH1（P1）与ML1（P1）。用PHm，PLm分别表示高成本与低成本垄断企业的单阶段垄断价格，MH1及ML1表示相应的垄断利润。可以假定MH1（P1）与ML1（P1）是严格凹函数，且PHm＞PLm，MH1＜ML1，第二阶段在企业2不进入的情况下，在位者收益与第一阶段垄断利润相同。

企业2选择进入后，假定企业1的类型就是公共知识，因此第二阶段两家企业竞争的价格与第一阶段的价格是独立的，用DH1与DL1表示两种类型企业1寡头竞争的收益，用DH2与DL2分别表示企业2面临高成本在位者与低成本在位者的收益。这也包含了企业2没有自己类型的私人信息的假设。显然，若DH2＞0，DL2＞0，则企业2必然会进入。企业1在第一阶段的任何价格不能阻止企业2的进入，对这种情况不需讨论。下面重点分析DH2＞0＞DL2的情况，即只有在位者是高成本的情况，企业2进入才是有利可图的。为了描述方便，假定贴现因子是1。

这是一个自然选择在位者类型，在位者第一期以价格作为信号的博弈。直观上，在位者会选择适当的价格，以影响进入者的决策。下面来分析各种均衡。

先考虑分离均衡，分离均衡的两个必要条件是高成本在位者不愿选择低成本在位者的价格，低成本在位者也不愿选择高成本在位者的价格。价格信号能精确区分在位者的类型，所以高成本在位者唯一最优选择是PH1＝PHm，即第一期获垄断利润。因为其他价格会减少第一期利润，但又达不到阻止进入的目的，同时，企业2的选择也不会使高成本的企业有更大的损失。高成本在位者的总收益是MH1＋DH1，这是高成本者的保底收益。

如果低成本在位者第一期选择PL1，进入者观察到PL1后不会进入，而高成本在位者也用PL1，来阻止进入是得不偿失的，这就要求成立：

上式的实际意义是高成本在位者用PL1虽然可以使进入者放弃进入，但在第二阶段的收益增加不能弥补第一阶段的发信号的成本损失。

PL1要满足（5.6.1）才可能出现分离。此外，对低成本在位者，过低的价格即使阻止了进入，也未必有利。阻止进入有意义的条件是

该式的实际意义是低成本者第一期垄断，而在第二期竞争的总收益是保底收益，任何有意义的信号其收益应该不少于保底收益。

如果低成本在位者的垄断价格PLm也不会招致高成本者模仿，则要求用PLm代入（5.6.1）中的PL1使式子成立。这时，在位者各自用垄断价就能分离。这一情况在成本差异较大时会出现。下面考虑更有趣的情况，低成本的垄断价不能分离，即

这表明高成本者第一阶段采用低成本者的垄断价格是有利可图的。

这时，满足（5.6.3）及（5.6.2）的PL1必成立PL1＜PLm。

满足（5.6.3）与（5.6.2）的PL1构成一个区间，即时使两式成立，否则至少有一式不成立。下面来证明，高成本者选择价格PHm，低成本者任意选择价格将会构成分离均衡。规定企业2的信念体系是P（H｜P1≠PHm， p L1）＝1。用贝叶斯法则可推得P（H｜PHm）＝1，P（H｜p L1）＝0，即企业2的信念是：偏离PHm，PL1的价格必是高成本企业。在这一信念体系下，参与人2的最优策略是，只有在PL1被观察时不进入，否则就进入。高成本在位者不会偏离是显然的。在位者不偏离的情况下，进入者企业2在PL1被观察时选择不进是最优的，因为P1≠PHm，P1≠PL1的前提下，依据战略是进入，如果偏离，选不进入，收益是0，而不偏离选进入的收益是

低成本在位者如果偏离PL1，则招致进入，收益为MH1（P1）＋DL1，不偏离p L1的收益为ML1（PL1）＋ML1，由于

这可由（5.6.2）式推得。因此，各方都不偏离。这一均衡使得PL1及PHm可以观察到，其它价格观察不到，即PL1及PHm在均衡路径上，其它价格不在均衡路径上。

以上分析表明，低成本者选择的价格在内部时都能构成分离均衡，但不能任由企业1选择，由企业2的信念规定了低成本1企业1的选择，可以看到低成本在位者的信号受到信念体系的逼迫。更确切地说，是受非均衡路径上的信念体系的逼迫。尽管低成本者在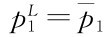时是最好的，而在p L1＝p1时最差，但偏离PL1被认为是高成本的信念限制了低成本者的选择。

由于非均衡路径上的信念只要求与战略相容，而与战略相容的信念很多，是否会有不合理的信念呢？

上面分析中，实际上是参与人2认定了只要不是p L1就是高成本的信念。这种信念是有不合理成份的。比如我们会想到既然P（L｜PL1）＝1，则p＜p L1时P（L｜p）＝1更合理，也就是说如果会选择更低的价格，这种企业不会是高成本的。

现在再来分析混同均衡。如果两类在位者选择同一价格，而又不能阻止进入，则低成本在位者还不如在第一阶段选垄断价，获得第二阶段的竞争收益好，所以存在混同均衡时，必成立

也就是存在混同均衡时，其混同信号不会使企业2选择进入。

如果p1是一个满足混同条件而两类型在位者都不会偏离的价格，则对低成本在位者仍然要求（5.6.2）成立，即混同优于垄断收益加上竞争收益的保底收益。对高成本者也有类似要求：

满足以上两式的p1构成一个区间。下面证明该区间的价格都可以成为混同均衡。为此，定义非均衡路径上的信念体系p（H｜p≠p1）＝1，即选择p1以外的价格必是高成本者。进入者观察到p1时不进入，否则就进入。这种信念体系下在位者偏离将导致进入，不如不偏离。而在位者不偏离时，进入者偏离无论在均衡路径上或是非均衡路径上均会减少收益，因为非均衡路径上的偏离是不进入，但依据信念，在位者是高成本的，当然进入比不进入好，而在均衡路径上，偏为进入是负收入，不进是零收益。所以，是混同均衡。

下面的图（5.10）是以上分析的直观示意。

图5.10 垄断限价博弈

可以看到，混同均衡也有多个。而一些混同均衡明显是不合理，这是非均衡路径上的信念引起的，后面将讨论这一类问题。

例5.6.2 下面是一个数字的例。参与人1有A、B两种类型，并且是私人信息，自然选择A的概率为0.5，参与人1有L，R两种信号，参与人2在接收到信号后可选择U，D，博弈树及收益如下图（5.11），求它的纯策略分离均衡与混同均衡。

图5.11 本例的博弈树

先考虑分离均衡。若信号可以区分参与人1的类型，B型参与人选R优于选L，因为B型的最大收益是2，而选L可实现这个最大收益，即分离均衡时B型参与人选R，既然B型选择R，两种类型又要分离，选不同的信号，所以A型参与人选L是分离均衡的唯一可能。由于信号直接观察了参与人1的类型，则对参与人2而言，相当于完全信息。因此参与人2在观察到L时选U，收益是2，否则，将导致收益为1，而观察到R时选D，收益为2，否则将导致收益为1。可以证明，这是分离均衡，其信念是P（B｜R）＝1，P（A｜L）＝1。若A型参与人1偏为R，则收益是1，不偏时收益是2，B型偏为L时收益为1，不偏收益为2。而参与人2也不会偏离。若R被观察，参与人2不偏的收益是2，偏为U时，收益是1，L被观察，不偏的收益是2，偏离收益是1。值得注意，该例中分离均衡与先验概率无关，即只要0＜P（A）＜1以上的分析结论都成立。

再考虑混同均衡。由于B型选L的最高收益还不如选R的最小收益，因此不论参与人2怎样行动，B型只会选择R，所以只能在R上混同。若两种类型的参与人都选R，则参与人2选U时他的收益是3×0.5＋0.5＝2，选D时0.5＋2×0.5＝1.5，所以参与人2应该选U。考虑非均衡路径，能约束参与人1不偏离R的信念是选L者必是A型，在此信念下，参与人2该在L出现时选U，即可以把参与人2的策略描述为“不论什么信号都选U”，非均衡路径上信念体系是P（A｜L）＝1，则任何人都不会偏离此均衡。

下面简要考察一下准分离均衡，由于B型选L是劣策略，所以只会选R。然而A型选L与R都可能，希望参与人2选U。若A型选R的概率是α，选L的概率是1－α，则(www.xing528.com)

参与人2在R被观察时选U的收益为

选D的收益为

则α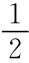＜时，因为2＋α＞3α＋1，所以参与人2在观察到R时不可能选U，只会选D。这时A型参与人1选R的收益是1，而直接选L。由于P（A｜L）＝1，参与人2会选U，两人收益均为2。所以不如α＝0的收益更高，这是分离均衡，所以α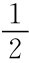＜时不存在分离均衡。

当α≥时，参与人2在观察到R时选U，A型参与人1选R的收益是3，选L时由于P（A｜L）＝1，参与人2会选U，两人收益均为2，所以不如α＝1的收益更高。

综上所述，不存在准分离均衡。

例5.6.3 斯宾塞得教育水平投资博弈

如果教育水平与人的能力无关（这当然是假设），人们是否会接受教育呢？许多时候，一个人的教育水平是用于显示他的潜能的，即教育程度作为显示能力的信号。教育水平用于显示能力的信号能起作用吗？这就要看高能力者选择高教育水平与低能力者选择低教育水平能否有分离均衡，如果存在分离均衡，则教育水平用于显示能力就是可行的。该例对这一问题进行建模分析。

把问题简化为一个雇员与一个雇主的博弈，参与人1是雇员，他具有能力类型的私人信息，是信号发送者；参与人2是雇主，为信号接收者，他希望付给雇员与能力相适应的工资，博弈顺序如下：

1）自然在Θ＝｛L，H｝中随机选择参与人1的类型，L记为低能力型，H为高能力型。参与人1知道自己的确切类型，而概率P（L）及P（H）分别是低能力型的先验概率，而且这是公共知识；

2）雇员以自己的教育水平作为发送的信号。假设教育水平e∈［0，＋∞］＝M可用数字描述，e越大表示接受教育水平越高，当然这是有成本的信号；

3）雇主观察到e后，在行动集A＝［0，＋∞］选择工资水平w；

4）雇员效用函数为U1（θ，e，w），雇主的效用函数为U2（θ，e，w）。

为了便于分析，假定能力可量化，设H＞L＞0。进一步，具体规定效用函数的形式，雇员的效用U1（θ，e，w）＝w－，这一形式中可理解为获得e教育水平的成本。这表明低能力者比高能力者投入更多才能获得相同的教育水平。假设雇主效用U2（θ，e，w）＝－（θ－w）2，这一形式中体现了能力与教育水平无关的假设。雇主的最优效用在U2＝0时取得，即支付给雇员与能力相适应的工资是最优选择。

下面分析该博弈的均衡，我们可以看到，问题的本质在于参与人是否承认教育水平作为能力的信号。

分离均衡：两种类型的雇员会选择不同的教育水平，而教育水平直接显示能力类型时，L型雇员只会选择e＝0（注意能力与教育水平无关的假设）。因为若e＞0，而仍然不能被雇主认为是高能力，因此得到L的工资。雇员效用为，不如直接显示e＝0效用更大。高能力的H型雇员会选择e＞0。然而这一e不能被L型模仿，意味着低能力者接受e的教育水平被认为高能力时的效用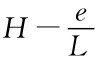还不如选e＝0好，即≤L或e≥L（H－L）。同样高能力者不会选e＝0，意味着H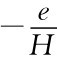≥L，即e≤H（H－L）。当e1∈［L（H－L），H（H－L）］时，成为分离条件。可以验证高能力者在此范围内的e1与低能力者选e1＝0能成为分离均衡。支持这一均衡的信念体系P（L｜e＝0）＝1；P（H｜e＝e1）＝1。当P（H｜e≠0；e≠e1）＝0，即任何不在e1教育水平的参与人1被认为是低能力型的人。这时任何类型的参与人都不会偏离均衡。

这表明，教育程度作为一种信号，能传达能力类型。这一均衡的实际体现是社会因教育水平的差异指定初聘时的工资水平，即使不同教育水平者放在同一岗位，仍因受教育程度的差异而形成工资差异。这是雇主接受信号的形式。

再分析一下混同均衡：假定两种类型都会选择同一种教育水平，由于混同，雇主无法更新先验分布，所以最优的工资是M＝P（L）×L＋P（H）×H。混同至少不会低于直接显示e＝0得L的收益，因此有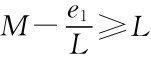，，，解得e1≤P（H）H（H－L）。如果信念体系是P（L｜e≠e1）＝1，即任何不在e1教育水平的参与人1都是低能力型的信念。则参与人1不会偏离e1而雇主也不会偏离。特别地e1＝0是混同均衡。在这一混同均衡下，各型雇员工资相同，参与人1都不接受教育，实际上信念体系拒绝教育水平作为能力的信号。所以，没有人会接受教育。

可以看到信念体系对均衡的支持的作用。该例子也表明了精炼贝叶斯均衡仍然有进一步再精炼的必要。如何在非均衡路径上添加更适当的条件，从而使精炼再精炼，能更合理地预测博弈的结果，是可以进一步研究的问题。

例5.6.4 博士录取博弈

博士录取博弈以学生提出申请作为信号，这一信号能否反应申请者对所申请专业的爱好？可以看到，参与人的信念对均衡的影响是关键的。

假设一所大学知道90％的人讨厌经济学，如果让他们读经济学博士课程，他们将会感到很郁闷。另有10％的人喜欢经济学，他们将会在经济学专业上取得好成绩。但申请者到底对经济学持什么态度，招生单位不知道，是申请者的私人信息。如果大学拒绝一个申请者，收益为0，申请者支付申请成本收益为－1。如果大学接受了某个讨厌经济学的学生的申请，学校与学生的支付各为－10，大学接受一个爱好经济学学生的申请，各方支付是＋20。博弈树如图（5.12）

图5.12 博士录取博弈

下面分析该博弈的均衡。

分离均衡：在分离均衡中，各型学生选择不同的行动。既然大学能知道申请者的类型，不爱好经济学的学生必被大学拒绝，所以他不会选择去申请，因此分离准衡如果存在，必是爱好者申请，不爱好者不申请。因而学校录取所有的申请者。在这种情况下，不存在参与人2即学校行动的非均衡路径。由于是分离均衡， P（H｜A）＝0或P（L｜A）＝1，即申请者必然是爱好经济学的学生是信念，也就是把提出申请看成是完全有效的信号。

混同均衡：在混同均衡中，不同类型的学生选择相同的行动。如果他们都选择申请，则学校接收的效用为20×0.1－10×0.9＝－7，拒绝的效用为0，因此拒绝所有的申请，学生申请的收益为－1，因此学生选择不申请的收益为0是更好的选择。这样两类型学生都不申请，学校拒绝任何申请是混同均衡。信念P（L｜A）＝u，简单地计算可知，只要u＜就支持混同均衡，学生提出申请在非均衡路径上。

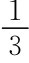如果以“混同时先验概率作为后验概率”方式调整信念，这时仍然是都不申请的均衡。到底怎样的信念体系是合理的呢？如果在均衡路径上，运用贝叶斯法则推断后验概率是公认的合理假设。然而，在非均衡路径上，贝叶斯公式是无法运用的，为使博弈分析更合理地预测行为，仅仅要求与战略相容看来是太弱的要求。可以附加一些外部的要求，对信念体系外加一些有意义的限制。比如在这一例中，所有学生都不申请成为混同均衡就意味着信念体系中P（L｜A）≤，即申请者中爱好经济学的人不超过，直观上这是不合理的。也许直观地，人们更倾向于认为，既然会选择申请，他爱好经济学的概率应该比较高，比如P（L｜A）≥0.6，即如果提出申请者是非均衡路径，非均衡路径上应该把P（L｜A）≥0.6作为一个外加的要求，这时就可排除都不申请的混同均衡。使爱好者申请，讨厌者不申请成为分离均衡。

对信念体系增加一些要求，使信念更合理是处理信念体系的一个常用方法。在各种对信念体系外加的要求中，被称为直观标准的准则经常被使用，它从这样的思路中引出，某种类型选择某个非均衡路径上的信号根本得不到收益改善，则就应该在这种非均衡路径上判断这一类型的概率为0。本例中，不爱好经济学的学生选择申请的收益总是低于不申请。因此应该判定P（H｜A）＝0或P（L｜A）＝1。这时爱好者申请，讨厌者不申请成为一个唯一的分离均衡。

该例可以看到，参与人的信念体系对均衡的影响。这也表明一种制度的设计，只有合理的信念体系，才能有好的结果。

注意：该例中假定讨厌经济学者被接受是负收益，主要强调信念的作用。如果厌恶者的申请被接受可获得正效用，比不申请好，则只有混同均衡。这表明，申请根本不能作为爱好判断的信号。

后面将对信念体系的合理性作进一步的讨论。