信号博弈的结构，信号博弈中的精炼贝叶斯均衡

信号博弈是最简单的不完全信息动态博弈。但有广泛的应用，从学习的角度看，信号博弈提供了深化理解不完全信息动态博弈的简明模型，本节对此进行讨论。

一、信号博弈的结构

信号博弈中有两个参与人，参与人1具有自己类型的私人信息，参与人2没有私人信息。参与人1发送信号，参与人2接收到参与人1发出的信号。参与人2的行动选择会影响参与人1的效用，而信号也影响参与人2的行动选择。博弈的顺序如下：

1）自然首先选择参与人1的类型θ∈Θ。我们讨论有k个类型的情况，即Θ＝｛θ1，θ2，…，θk｝。参与人1知道自己的类型，但参与人2只知道参与人1类型的概率分布p（θi），当然p（θ1）＋…＋p（θi）＝1，而且p（θi）是公共知识。

2）参与人1在自然选择之后选择发出一个信号，所有可选择的信号称为信号空间，记为M，M＝｛m1，m2，…，m T｝。

3）参与人2观察到参与人1发出的信号m∈M后，选择行动。行动空间是A＝｛a1，a2，…，aτ｝

4）若θ型的参与人1发出信号m，参与人2选择行动a，参与人1的效用为u1（θ，m，a），参与人2的效用为u2（θ，m，a），效用函数是公共知识。

信号博弈中涉及到对信号的处理，参与人1的问题如何选择信号，参与人2的问题是对发出信号m的参与人1类型的判断，即条件概率P（θ｜m）的计算，这构成一个后验的信念体系。假设两个参与人具有相同的信念体系P（θ｜m）且是公共知识，参与人2知道以P（θ｜m）方式利用信息，参与人1知道信号接收者会这样利用信息。

二、信号博弈中的精炼贝叶斯均衡

一般精炼贝叶斯均衡的概念适用于信号博弈，但因信号博弈简明的特性，可以给出均衡的更具体的形式：发信号者的战略是类型依存在的，可以记为m（θ），而信号接收者的战略是依据所有可能的信号，确定选择行动的规则，可用a（m）标记。

定义5.5.1 信号博弈的精炼贝叶斯均衡是战略组合m＊（θ），a＊（m），及后验概率p（θi｜m）体系，使下面的条件成立。

2）u1（m，a＊（m），θ）≤u1（m＊，a＊（m），θ），∀m∈M

3）p（θi｜m）是信号发送者以m＊（θ）发送信号时用贝叶斯法则从先验概率得到的后验概率。

条件3）中，是贝叶斯公式的表达式，该式有意义的要求是分母：

＝p（m）＞0，即m以正的概率出现，否则贝叶斯公式无法应用，当m不以正概率出现，即依据最优策略不会选择的信号，只要求信念的后验概率p（θi｜m）与战略相容。

条件1是指，参与人2的战略在所有的信息集中是最优的，即对于任意m， a＊（m）是最优的。但是，参与人1选择m是参与人2信息集的前提信息。这与一般的不完全信息博弈的表达是有差异的。因为进入信息集之后，只有参与人2有行动机会了。

信号博弈的所有可能的精炼贝叶斯均衡有什么规律呢？可以归纳为三类均衡，并且这三类均衡的直观含义很清楚：

某些类型的信号发出者希望隐藏自己的类型，混同于另一些类型，而先验信息使被混同的类型不造成损失，这类均衡称为混同均衡。

各种类型的发送者发出不同的信号，信号直接能判断出发送者的类型，称为分离均衡。

某些信号能判断出发送者的类型，但某些信号造成混同，称为准分离均衡。

下面分别介绍这些均衡。

混同均衡：不同类型的发送者选择的策略是发送相同信号。因此，信号的接受者在接收到信号后没有有效地信息能改进先验概率。即在贝叶斯法则下对参与人1的类型判断的后验概率等同于先验概率。假如均衡战略是纯战略，每一类型的信号发送者发出mi0的信号，则

对每一类型的信号发送者，要求成立

u1（mi0，a＊（m），θi）≥u1（m，a＊（m），θi）， i＝1，…，k

我们也可以考虑非纯策略，即混合策略的均衡，实际上，混合策略的混合均衡是各种类型的参与人1都以相同的概率选择某种信号，因为若

则成立下式：

分离均衡：不同类型的发送者选择相同信号的概率为零，而且这样的选择对各个类型的参与人1都是最优的。

若θi类型的参与人1的信号是Mi⊂M，则Mi∩Mj＝Φ（i≠j），即各类型的参与人1各有一个其他类型的信号发送者不会选择的信号集，则对每一类型参与人1有：

式（5.5.1）表示θi类型的参与人1不会选Mi以外的信号，式（5.5.2）表明在Mi中的信号是无差异的。

当Mi不止一个元素时，后验信念是

p（θi｜m∈Mi）＝1； i＝1，…，k(www.xing528.com)

准分离均衡：这是处在混同与分离之间的情况。

准分离信号，本质上是某些类型参与人既可以采用混同，也可以采用分离信号，而且都不影响收益。

如果满足（5.5.1）、（5.5.2）的Mi不是互相分离的，至少有Mi∩Mj＝Φ（i≠j）。但也不是Mi＝Mj（i≠j）。

后验信念是当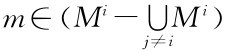时，p（θi｜m）＝1。对于其他的信号，即m是某些类型的共同信号，而另一些类型不会发的信号。不会发送m的参与人1的类型的后验概率是零，会发送m的参与人1的类型有一个按贝叶斯公式计算的调整。

准分离均衡中，对某些类型的共同信号，后验概率由参与人在Mi中的取各种信号的概率分布决定，按贝叶斯法则计算得到。

应用中，Mi是单一元素的情况较普遍，前面的三种均衡类型需注意到是必要条件，而且由于定义中使用了a＊（m），因此隐含地包括了非均衡路径上的一些需要保证是均衡的后验信念。这给求均衡带来很大的困难。当然用于检验某一策略组合在某一信念下是否为均衡并不成问题。但是，要在先验概率下求出均衡却有困难。实际上，这些困难产生于非均衡路径上后验概率的随意性。

三、信号博弈均衡分析的思路

由于信号博弈的均衡对信念体系的依赖性很强，往往是博弈在非均衡路径上的信念的改变，就会使均衡变成非均衡。而非均衡路径上的信念又是不能用贝叶斯法则计算的，事实上有很大的自由度。因此，给定博弈，给定先验概率，求均衡的条件是不够的。这导致博弈求解的困难。下面我们讨论信号博弈的均衡与后验信念无关的一些特征。这些特征有助于求解均衡。

信号的发出方，θi类型的参与人1会发出何种信号呢？下面讨论参与人1会选择发出某种信号的基本要求。

例如在5.3.1节的市场进入博弈中，高成本在位者不会选择价格4，低成本在位者不会选择价格6，否则与基本的理性矛盾。

若θi型发出信号m，则记

上式的数值是θi型参与人1发出m信号的最少收益，参与人2的其他策略只会使参与人1收益增加，所以如果选择信号m使

则，θi）是θi型参与人1能够在任何情况下都能够得到的收益，称为保底收益，即只要选信号m，至少有U1（m，a（m），θi）收益，简记为U1（θi），如果

U1（m，a＊（m），θi）＜，θi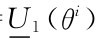）＝，那么，m信号是θi的参与人不应该选择的信号，因为收益低于保底收益。如果

由于U1（m，a＊（m），θi）≤（m，a，θi），所以上式成立的m肯定是θi不会选的信号。

利用（5.5.3），可计算m的范围，这就是均衡信号不可能的范围，由 。可计算出Mi，这一Mi是θi的可能发出信号范围，即不在这一范围内的信号，θi不会选择。若对各个类型计算M1，M2，…，MK，若Mi∩Mj＝Φ，则该博弈只有分离均衡，因为会选的信号已经分离。

下面对信号发送者两个类型的情况进行讨论。

显然，M1∩M2＝Φ，只有分离均衡，而M1∩M2≠Φ是混同均衡的必要条件。

利用先验概率，分析混同均衡的特点。混同均衡存在于M1∩M2之中。若m∈M1∩M2。当m1≠m时，对某一类型θi，在参与人2知道θi条件下的最优解α＊（m1，θi）使得成立。

U1（m1，a＊（m1，θi），θ1）≤U1（m，a＊（m），θ1） U1（m1，a＊（m1，θi），θ2）≤U1（m，a＊（m），θ2）

则m必为混同均衡。这主要是因为在非均衡路径上可规定P（θi｜m1≠m）＝1导致每一参与人都不会偏离，因为一旦偏离，判断成对参与人1最不利的类型导致不敢偏离。

注意上式中a＊（m）与a＊（m，θi）的差异。a＊（m，θi）是已知θi类型时参与人2的最优策略，而a＊（m）是综合各种类型在先验概率下的最优。

上述混同是被非均衡路径上的信念体系强迫而造成的均衡。

对于分离均衡，θ1型参与人1的信号在M1－M2中，θ2型参与人1的信号在M2－M1中，若m1∈M1－M2，且U1（m1，a＊（m，θ2），θ2）＜，则不可能成为均衡信号，即M1－M2中只有参与人2已知类型时所选的策略使θ1型参与人1的收益不少于保底信号，才可能成为均衡。对m1∈M1－M2，仍然也要求θ2型参与人1的收益不少于保底收益。

记类型被认别时收益超过保底收益的θ1型参与人的信号集为M¯1，同理记¯M2。如果在¯M1中类型被误判不会减少收益，则只有在¯M1中的M＊使

才可能是分离均衡信号，这时后验概率

当中类型被误判导致损失时即成立

U1（m＊，a＊（m，θ2），θ1）＜U1（m，a＊（m，θ1），θ1）

这种情况下，中的每一个信号m成为均衡信号。后验概率是P（θ1｜m）＝1，P（θ2｜m1≠m，m∈¯M1）＝1对θ2型的参与人1情况类似。

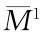综上，信号博弈的均衡分析可从保底收益入手，求出M1，M2；在M1∩M2中分析存在混同均衡的可能；在M1－M2与M2－M1中，依据类型识别后的收益不少于保底收益分别计算与；⊂M1－M2；⊂M2－M1，再在与中分析误判是否导致损失，判断分离均衡。这可以作为信号博弈均衡分析的一般思路。