不完美信息博弈的均衡介绍

不完全信息动态博弈是一种不完美信息动态博弈，然而信息不完美可能是观察不到先行动者的行动造成的。但在引入信息集的概念后，这种差异在分析上并不引起更多的困难，因为参与人类型的后验概率等价于信息集中处于哪个决策结的概率，所以后验信念落实到信息集之后不完全信息与不完美信息的差别就不重要了。本节用几个例子简要介绍不完美信息动态博弈，更主要的目的是加深对信息集及后验信念的理解。对不完美信息，精炼贝叶斯均衡的概念仍然是有意义的。

观察图5.6所描述的不完美信息博弈

图5.6 不完美信息博弈

该博弈有2个人参与，参与人1先行动，如果选择L，则博弈结束。如果不选择L，则在参与人1选择后由参与人2在不知道参与人1选择结果的情况下进行选择。所以L的选择可区分，没有参与人2选择的机会就意味着参与人1选了L，而参与人2在轮到他选择时，知道参与人1已选择了M或R，但没有更多的信息，所以有一个两个决策结构成的信息集。

这个博弈有两个纯战略纳什均衡（M，U）和（L，B），这可以用纳什均衡的定义直接验证。我们来考察（L，B），由于该博弈没有非平凡的子博弈，唯一子博弈就是博弈本身。因此（L，B）是子博弈精炼纳什均衡。用此预测参与人的行为合理吗？我们知道完全信息动态博弈中子博弈精炼纳什均衡是合理的。但在不完全信息动态博弈中，又有了新的问题。实际上（L，B）这一均衡中包含了参与人2的不可置信威胁，参与人2承诺“我有机会就选B”，参与人1因害怕而选L。因为参与人2实现承诺时参与人1的收益是零，所以选了L。但若参与人1选了M或R后，参与人2放弃B而选U是更优的，所以承诺不可信。这表明在不完美信息动态博弈中，子博弈精炼纳什均衡还不能排除不可置信的威胁。

然而，如果用精炼贝叶斯均衡的概念来分析，可以发现（L，B）在任何信念体系下，都不能构成精炼贝叶斯均衡：若（L，B）战略组合是精炼贝叶斯均衡，则参与人2没有选择机会，即参与人2选择的信息集不在均衡路径上。按定义只要有与战略相容的后验概率，但任何后验概率都不会使参与人2选B是最优的，若参与人选择M的概率为p，选择R的概率为1－p，则在参与人2选择的信息集为起点的博弈中，参与人2选B的收益应该比选U的收益大。然而选B时的收益是0＋（1－p）＝1－p，而选U时的收益是p＋2（1－p）＝2－p：由于2－p＞1－p。这表明参与人2在他选择的信息集为起点的博弈中，他的选择不是最优的，按定义（L，B）不是精炼贝叶斯均衡。

我们再来检验（M，U）能否构成精炼贝叶斯均衡：给定参与人2选U，则参与人1选M是最优的，因此参与人1不会偏离。在参与人2选择的信息集中，既然参与人1选M，则贝叶斯法则决定左边一个决策结的概率是1，则参与人选B的收益为0，选U的收益是1。因此参与人2不会偏离。因此（M，U∶P＝1）是一个精炼贝叶斯均衡。

对此博弈，也可分析一下混合策略均衡。实际上，参与人2在其选择的信息集中，任何后验概率下，选U比选B好，所以只要有选择的机会，只会选U而不会选B。而在此基础上参与人1以任何正的概率选L或R都会比选M时的收益少。所以不会有混合策略精炼贝叶斯均衡。

具体地，若参与人1以α1的概率选L，α2的概率选M，α3的概率选R，参与人2以β1与β2的概率选U与B时，如果是最优策略，则进入参与人2的信息集左边决策结的概率是，右边决策结的概率是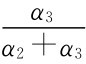，参与人2的收益是

所以β1＝1时是最优的，即最优的混合策略是β＊1＝1，β＊2＝0。这时，参与人1的收益是

α1＋2α2＋0×α3＝1＋（α2－α3）

所以α2＝1时取最大，α＊1＝0，α＊2＝1，α＊3＝0，因此，没有混合策略均衡。

下面把囚犯困境作为不完美信息博弈来分析精炼贝叶斯均衡。参与人2选择的信息集上若左边的决策结的概率为p，则参与人2选T的收益为－3×p＝－3p。

参与人2选D的收益为－5p－（1－p）＝－4p－1。

图5.7 不完美信息囚徒困境

所以不论p为何值，T是最优选择，而参与人1在参与人2的最优策略下，选T的收益是－3，选D的收益是－5，因此（T，T，p＝1）是一个精炼贝叶斯均衡。(www.xing528.com)

再分析图5.8的协调博弈。用静态博弈来分析时，很容易得到（T，T），（D，D）及混合策略是纳什均衡。该博弈是否有精炼贝叶斯均衡呢？

图5.8 协调博弈的博弈树

博弈肯定会进入参与人2的信息集，即参与人2的信息集总在均衡路径上。

先考虑纯战略，则p＝0或p＝1。给定p＝1的信念，即参与人1选T为最优时，参与人2选T收益是1，选D的收益为1×0＋0×2＝0，所以（T，T，p＝1）是精炼贝叶斯均衡。同理（D，D，p＝0）也是精炼贝叶斯均衡。

再考虑混合战略，若0＜p＜1，即参与人1选T的概率为p，则左边的决策结的概率为p，如果参与人2选T的概率是q，则他选T的收益为p，选D的收益为2（1－p）。混合战略均衡要求p＝2（1－p），即p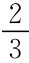＝。对参与人1，选T的收益是q，选D的收益是2（1－q），要求q＝2（1－q），即q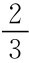＝，即混合策略也是精炼贝叶斯均衡。

下面举一个有三个参与人的不完美信息博弈的例子，如图5.9所示。这一例子中，参与人1先行动，参与人2在参与人1行动后行动。参与人2必定知道参与人1的行动。参与人3最后行动，但他不能区分是参与人1选了L还是参与人1选R，再由参与人2选U后的结果，即所知信息是参与人2没有选B。参与人2选择的信息集是单结，参与人3选择的信息集是二个结。

图5.9 三人博弈例子

可以验证（L，B，A）是一个纳什均衡，因为任何人单方面偏离都导致损失。

但这个纳什均衡用于预测博弈结果时可能不太合理。因为包含了参与人2的不可置信承诺。当博弈如果进入参与人2的信息集作为博弈的起点，而参与人3又坚持选A时，参与人2放弃B而选U时，效用从3变为5。由于（L，B，A）战略组合下，参与人2的信息集不在均衡路径上，或说出现参与人2行动的信息集的概率是0。从这一决策结开始的博弈并不是一个子博弈，所以（L，B，A）还是子博弈精炼纳什均衡。然而这一均衡结果不是精炼贝叶斯均衡的结果。当博弈进入②决策结作为前提信息，而战略的剩余的可执行部分有参与人2的选择。若参与人3的选择不变，仍然坚持选A，则参与人2把B变为U是更优的。所以不是精炼贝叶斯均衡。对参与人3而言，涉及到两个决策结中的概率分布的信念，在很大程度上，参与人3选A是合理的。如果他相信右边决策结的概率比大，选A优于D。

如果参与人1选L，参与人2选B是最优的，则参与人3处于右边决策结的概率为1的信念是合理的。但参与人2选B具有不合理性时，这一信念就包含了不合理的因素，也就是说，依据非理性的策略，合理推导的信念也是不合理的。

在此，我们看到了战略、信念之间的循环关系。

下面再分析一下是否有参与人3选D的均衡：若参与人1选L，不可能构成参与人选D的均衡。因为参与人2的选择不论是什么，参与人3会偏向A。两种可能的情况是（R，U，D）与（R，B，D），但（R，U，D）中，参与人1、3不变时，参与人2会偏离。所以也不可能是均衡结果。可以验证（R，B，D）是纳什均衡。这一均衡是否为精炼贝叶斯均衡呢？按这一策略组合，参与人3的信息集不在均衡路径上。贝叶斯法则无法处理两个决策结的概率分布。与参与人3选D相容的信念是p＞，因此，（R，B，D，p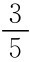＞）是精炼贝叶斯均衡。

注意一下，这一贝叶斯均衡，我们可能替参与人3叫屈，得不到任何收益，是信念体系使他得不到任何收益的。表明了信念体系的重要意义。

可以验证（L，U，A）不是纳什均衡，因为参与人1在知道U、A时会偏向R。