精炼贝叶斯纳什均衡的分析介绍

由于动态博弈中先行动者的行动不能完全观察，且涉及一个参与人多次行动时，会涉及很复杂的情况。下面只对经典范围的不完全信息动态博弈进行讨论，后面讨论的不完全信息动态博弈主要是指以下特征的动态博弈：

1）自然首先选择了参与人的类型，参与人知道自己的类型，不确知其他人的类型。

2）参与人在自然选择后有行动的先后顺序。

3）后行动的参与人可以观察到先行动的参与人的行动选择。

这类博弈，信息不完美唯一的来源是自然的选择。它不包括其他参与人的行动只有部分信息的情况。作为后行动者，尽管不能确定先行动者的类型，但通过观察到的先行动者已选择的行动，可以获得一些关于先行动参与人类型的信息，因为不同类型的参与人会对不同的行动有偏好，行动选择的结果中包含着已行动的参与人是什么类型的信息。后行动者可以用已观察到的行动来推断参与人类型。作为先行者，知道自己的行动将被后行动者利用。因此就需要在选择行动时考虑后行动者可观察自己行动的优势，在自己选择行动时需注意后行动者的对策。

如果自然选择参与人类型是随机的，并且分布函数是公共知识，自然随机选择的概率为先验信念或先验概率。当某一参与人选择了行动后，后行动者将会根据先行动者的行动来修正参与人的类型分布，被修正后的类型分布概率称为后验信念或后验概率。很显然，会想到运用贝叶斯法则来进行推断。

分析不完全信息动态博弈的目的仍然是求均衡，精炼贝叶斯均衡是不完全信息动态博弈中的基本均衡概念。由于完全信息动态博弈是其特例，因此，这一均衡将容纳子博弈精炼纳什均衡，是子博弈精炼纳什均衡的推广形式。

同时，静态贝叶斯均衡中的处理方法也被吸收。下面先对一个具体例子来进行讨论。

一、市场进入博弈

设在时期1，企业1是市场的垄断者，称为在位者。他的生产成本是私人信息，一个潜在的进入者考虑是否在时期2进入该市场。如果不进入，在位者仍然可以获得垄断利润。如果进入，两企业进行库诺特寡头竞争。

假设在位者的成本有高低两种类型。进入者只知道在位者高成本的概率为α，低成本的概率为1－α，这可以理解为自然选择了高成本或低成本的在位者，并且是随机选择的，以α的概率选择高成本在位者，这一概率分布是进入者企业2的先验概率。对进入者的成本假定只有一个类型，与高成本的在位者相同，企业2如果选择进入，进入的不变成本为2。

为了突出分析的基本原理，对价格作离散化的处理，假设在位者在第一期的策略空间为4，5，6这三种价格。对应三种价格的利润如表5.1。

表5.1 在位者一期收益与价格

在时期2，如果进入者已进入，则在位者的成本成为公共知识。在这种假设下，进入后的分析就比较简单了。如果都是高成本者，均衡价格是5，每一企业的利润为3，进入者扣除进入成本的收益为1。若在位者是低成本的，均衡价格是4，在位者利润为5，进入者利润为1，扣除进入成本后收益是－1。进入者不进入时，企业1在时期2仍然可以垄断经营。

在位者以两期的经营总收益为目标，他不能不考虑两期收益的相互影响，比如高成本在位者第一期以价格6出售产品，则它是高成本的类型就完全暴露了，必将导致进入者的进入，所以尽管第一期可以获取垄断利润，但导致第二期的利润损失，因此不是整体最优的。

该博弈的过程可描述成下图的时间线。

图5.4 进入博弈的时间线

由于在第二期，进入者做出进入或不进入的选择后，已经有了直接的结果。该博弈的分析可把进入者的选择作为最后阶段，可以描述成图5.5。

图5.5 市场进入的动态博弈树

博弈双方需思考的问题有：

1）在位者不能独立地处理这两个阶段，两个阶段是一个整体。如为了获得第一阶段的垄断利润，高成本的在位者以价格6出售产品。进入者就能判断出在位者是高成本的，因为低成本时，价格5是最优的垄断价格，低成本者不可能选择6。所以高成本者可能陷于第二阶段的不利局面。

2）在位者如何来给出第一期的价格呢？即使第一期少收益，如果能使进入者不进入，可能还是有利可图的。

3）进入者观察到在位者第一期的经营价格，就要充分利用这一信息，以使自己做出最优的选择。

4）如果在位者第一期的价格不是理性思考后的选择，这时信息是无价值的，在假定理性人的条件下，我们可以认定在位者的第一期的价格是理性决策的结果，而进入者也将以理性的方法运用在位者第一期的价格信息进行决策。

5）对在位者的最优决策，进入者可用贝叶斯方法来运用第一期的价格信息，以改进在位者的类型信息。

下面分析几种情况来讨论该问题：

1）在位者第一阶段选择垄断价格不是最优策略

如果高成本者选p＝6，低成本者选p＝5是最优策略，依据这一策略，有如下的条件概率：

p（4｜高成本）＝0；p（5｜高成本）＝0；p（6｜高成本）＝1

p（4｜低成本）＝0；p（5｜低成本）＝1；p（6｜低成本）＝0

运用贝叶斯公式，可以对在位者类型进行修正，计算出在位者类型的后验概率：

p（高成本｜6）＝ p（高成本）p（6｜高成本）p（高成本）p（6｜高成本）＋p（低成本）p（6｜低成本）＝ αα＋（1－α）×0＝1

同理可得：p（低成本｜5）＝1

进入者采取“p＝6被观察就进入，否则不进入”的策略是最优的，因为当价格6被观察时，进入者的期望收益是

EU2＝p（高成本｜6）×u2（高，高，进）＋p（低成本｜6）×u2（低，高，进）＝1

不进入的收益为0。

当价格5被观察到时，进入者不进的期望收益为：

EU2＝p（高成本｜5）×u2（高，高，不进）＋p（低成本｜5）×u2（低，高，不进）＝0

而选择进入时的收益是－1。

然而对高成本的在位者，若第一阶段选择价格5而不是价格6。进入者依据战略是不进入。这样，高成本在位者第一期收益是6，而第二期可获垄断收益7，总收益为13，这比“第一阶段垄断收益7，第二期竞争收益3”的总收益10要好，这说明了各类型的在位者各自取垄断价格经营不可能是最优策略。

下面我们来验证最优策略，仍然分几种情况来讨论。

2）α＜的情况

在位者“在第一阶段选p＝5”；进入者“p＝6被观察就进入，否则不进入”这一策略组合是最优的，最优的含义是单方面偏离将导致损失。

依据在位者的策略可得：

p（4｜高成本）＝0；p（5｜高成本）＝1；p（6｜高成本）＝0

p（4｜低成本）＝0；p（5｜低成本）＝1；p（6｜低成本）＝0

而

p（低成本｜5）＝1－α

这表明，在位者的策略使得进入者没有获得改进在位者类型判断的有效信息，进入者只能利用先验概率做出是否进入的决策。就是说，在这一背景下，进入者相当于观察不到在位者行动的情况，在观察到价格5不进入的收益是：

EU2＝p（高成本｜5）×u2（高，高，不进）＋p（低成本｜5）×u2（低，高，不进）＝0(www.xing528.com)

而观察到价格5与选择进入的收益是

EU2＝p（高成本｜5）×u2（高，高，进）＋p（低成本｜5）×u2（低，高，进）

＝α×1＋（1－α）（－1）＝2α－1

由于α＜的假设，因此2α－1＜0，所以进入者观察到5时不进入是最优策略。

高成本的在位者，是否会偏离在一阶段选价格5的策略呢？若高成本在位者

第一阶段价格是4，收益是2，第二阶段垄断收益为7，总收益是9；

第一阶段价格是6，收益是7，第二阶段竞争收益为3，总收益是10；

第一阶段价格是5，收益是6，第二阶段垄断收益为7，总收益是13。

所以，高成本的在位者不会偏离第一阶段价格5的策略。

同理，对低成本的在位者，也不会偏离第一阶段价格5的策略。

因此，在α＜时，即高成本的可能性比低成本的可能性小时，均衡路径是第一阶段在位者以价格5出售产品，进入者不进入，在位者在第二阶段垄断经营。

这种情况下，第一阶段的价格4，6是不会出现的，也即价格4与6在非均衡路径上，这时p（高成本｜6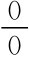）＝或p（高成本｜6）不能定义。但依据战略，如果价格6被观察，则进入者选择进入是最优的，进入时的收益是

EU2＝p（高成本｜6）×u2（高，高，进）＋p（低成本｜6）×u2（低，高，进）

＝p（高成本｜6）×1＋（1－p（高成本｜6））（－1）

＝2×p（高成本｜6）－1

不进入的收益为0，价格6被观察进入是最优意味着2×p（高成本｜6）－1≥0，所以在战略中隐含了p（高成本｜6）≥的假设。

关于在非均衡路径上的后验概率，贝叶斯法则是无法直接应用的。非均衡路径在实际的博弈中不会出现，为什么还要讨论呢？我们在完全信息动态博弈中见到过类似情况，我们可以回忆起，非均衡路径上的子博弈具有重要意义，因而引出了子博弈精炼纳什均衡的概念，使不可置信的威胁得以排除，不完全信息动态博弈非均衡路径上的后验概率也有类似的作用，这将在后面讨论。

在α＜时的最优策略，实际上由于先验概率中高成本的可能性小，使得进入者在没有进一步信息时不进入是最优的，在位者知道这一点，高成本的在位者在第一阶段装出低成本的样子，使自己得利。很显然，若高成本的可能性更大时，就不存在浑水摸鱼的策略。若高成本先验概率较大时，低成本者可能要有意显示自己的类型，以阻止进入者进入。

3）α≥的情况

若在位者都选择价格5，尽管进入者没有改进类型判断的信息，然而没有进一步信息时进入者选择进入是最优的，考虑到这一点，低成本的在位者可能需要花代价以显示自己是低成本的，以获得第二阶段的垄断收益。

下面来证明：高成本在位者在第一阶段选价格6，低成本在位者选价格4，进入者“若观察不到价格4，就选择进入”是最优策略组合。

依据在位者战略可得

若低成本者选择价格4，进入者不进入，可计算得低成本在位者的收益。

第一阶段价格是4，收益是6，第二阶段垄断收益为9，总收益是15。

第一阶段价格是5，收益是9，第二阶段竞争收益为5，总收益是14。

第一阶段价格是6，收益是8，第二阶段竞争收益为5，总收益是13。

所以低成本在位者不会偏离第一阶段价格4的策略。

对高成本在位者而言：

第一阶段选价格4，收益为2，第二阶段垄断收益为7，总收益是9；

第一阶段选价格5，收益为6，第二阶段竞争收益为3，总收益是9；

第一阶段选价格6，收益为7，第二阶段竞争收益为3，总收益是10。

所以高成本在位者不会偏离第一阶段价格6的策略。

同样，进入者坚持策略的收益是：当价格4被观察时进入的收益是－1，不进的收益是0。当价格6被观察时进入的收益是1，不进的收益是－1，所以进入者不会偏离他的策略。价格5不在均衡路径上，进入者在观察到价格5要选择进入的策略也隐含了p（高成本｜5）≥1／2的信念。

当α≥1／2时的最优策略表明，由于先验信息对低成本者不利，必须要有实际行动来表明自己的低成本类型，在这种情况下，高成本者再混同于低成本企业的行为代价太高，以至于不如直接获取第一阶段的垄断收益更好。

对该例的分析，我们在没有明确定义均衡概念的背景下进行的。使用的最优是指某人单方面偏离将导致损失的意义下分析的。而进入者对在位者的类型判断是依据在位者的策略，用贝叶斯原理推断的，而在贝叶斯法则不能应用的场合，只要求与战略不矛盾来规定。下面我们来引出不完全信息动态博弈均衡的定义。

二、精炼贝叶斯均衡

一般地，对不完全信息动态博弈，需要讨论适合它的均衡概念。注意到参与人行动之前由于已行动参与人所选择的行动是可观察的，某一参与人行动时，需要考虑这些信息的运用。直观地说，均衡战略应该在任何信息集为始点的后面的博弈过程中，在后验概率分布下的期望收益是最优的。

在我们假定自然对参与人的类型的分布是公共知识，而先行动者的行动可观察的条件下，每一个信息集中的决策结，虽然不能具体确定是哪一个决策结，但是可以产生信息集中决策结的概率分布。运用静态贝叶斯博弈中的方法，可以要求在后验概率下的期望收益最大化。

实际上，对参与人类型的后验概率或后验信念本质上就是各个信息集中各个决策结的后验概率分布。因此，信息集上的信念的确定意味着对类型的后验信念的确定。

用博弈已进行的行动选择来修正参与人的类型的判断。如果前面参与人的行动不是理性的选择，这可能无法运用已进行的博弈的信息，找不到利用信息的方法。如在前面的例子中，低成本在位者以的概率选任一种价格，这时进入者观察到价格6的概率是正的。显然包含了在位者的非理性行动，难以进行理论的讨论。所以我们需限定在理性的行动与理性的信息运用的基础上来讨论均衡问题。

理性行动假设下，某些信息集不会出现，即某些信息集在非均衡路径上。但分析时，战略要对任一信息集作为逻辑起点的分析有意义（这与完全信息中从任一子博弈作为起点相似）。贝叶斯公式本身无法确定非均衡路径上信息集中决策结的概率分布，因为非均衡路径上的信息集出现的概率为零，即贝叶斯公式的分母为零。因此，作为附加要求，相应的参与人对非均衡路径上的信息集要规定与战略相容的后验概率。这样，在每一个信息集上，都有了处于哪个决策结的概率分布，而这种分布是经过推断及主观观念规定的。所有信息集上的后验概率，称为信念体系。

设有n个参与人，参与人i的类型θi∈Θi是i自己知道而其他参与人不确知的信息，但i知道自己类型时，可获得其他参与人的类型θ－i＝（θ1，…，θi－1，θi＋1，…，θn）的先验概率pi（θ－i｜θi），Si是i的战略空间，si∈Si是一个具体战略，参与人i行动时的信息集是h，用表示已经行动的参与人行动选择的观察结果，它是战略组合的输出，其它参与人类型的后验概率是。参与人行动时，可能面临着若干个信息集，对每一信息集，规定后验概率并记为，参与人i的效用函数是ui（si，s－i，θi，θ－i），则有下面的精炼贝叶斯均衡的定义。

定义5.3.1 n人不完全信息动态博弈的精炼贝叶斯均衡是指一个战略组合s＊（θ）＝（s＊1（θ1），…，s＊n（θn）及一个后验概率组合满足下面条件：

1）参与人i，在每一信息集上

2）是依据ah－i和最优策略s＊－i从先验概率通过贝叶斯法则得到的后验概率。（在贝叶斯法则无法应用时，要求与战略相容）

以上定义中，比较抽象的是不完全信息动态博弈中的战略，如果阶段多，战略描述可能会很复杂。每一参与人的一种战略要对每个信息集指定选择规则，而战略空间则是所有可能规则的集合，因此，会出现很多的战略。

定义中的1）实际上是对信息集中依据后验概率的最优性要求，这时要注意一个问题，最优战略可能使某些信息集不出现在均衡路径上，战略组合在非均衡路径上的信息集为起点的博弈中要规定它的含义，这与完全信息动态博弈的情况类似，在完全信息动态博弈中，子博弈的条件优先于战略路径。类似地，在信息集之后的博弈中，信息集成立的前提条件优先于战略组合的路径，战略在此信息集之后的博弈中的意义是指以信息集的前提为条件，战略的可执行部分的路径。

如果从验证的角度，就比较好理解精炼贝叶斯均衡。某一战略组合 是否为精炼贝叶斯均衡，可以依据战略，推算最下层的信息集的后验概率，且要求最下层的信息集以下的博弈构成精炼贝叶斯均衡。由此可减少一个博弈阶段，再往上推，可以验证战略组合是否为精炼贝叶斯均衡。

然而不能希望用逆向归纳法求出精炼贝叶斯均衡，因为无法给定后验概率时，最下层的静态贝叶斯均衡就无法计算。既然精炼贝叶斯均衡无法简单地计算出来，我们自然会关心精炼贝叶斯均衡的存在性问题。对有限博弈，存在性已经得到了证明。