模型的特征与描述，动态博弈中的不完美信息

一、动态博弈中的不完美信息

下面先讨论不完美信息与信息集的概念。

在完全信息动态博弈模型中，我们介绍了描述博弈的扩张式方法，也就是博弈树方法，主要讨论的是某个参与人行动前，有足够的信息来确定已经行动的参与人选择了什么行动，这种信息结构称为完美信息。当博弈的参与人只行动一次，后行动者没有任何先行动者的信息时，我们可以把这种情况等效于静态博弈。不完美信息指的是这两种背景之间的情况，即有一部分已行动者所选行动的信息，但又不能完全确定先行者选择了什么。

反映先行动者选择的信息，可能是千差万别的，会有各种形态的信息。如在猜硬币游戏中，一个盖住硬币，一人猜。盖的人先行动，已经指出过，对盖什么的选择结果毫无信息时，对猜的人而言，等效于同时行动。当你作为猜的一方，在博弈中可能会很注意观察对方的行动细节，指望这些观察中获得有用的信息。极端情况是结果被你看到了，这就是完美信息了。但许多信息可能对结果是什么的可能性的判断有帮助，而具体结果不能完全确定。我们不去关注具体的信息是什么，转而关注信息所反映的先行动者的选择结果。在博弈树中，就是在后行动者行动前，到底处于哪个决策结的问题。如图5.1所示的猜硬币博弈，各种信息的结果都反应在左右两个决策结的判断中。

图5.1 猜硬币的游戏

在参与人2行动的决策结，如果你已知道是什么结果，则左右两个决策结不会混同。足以使你知道那个决策结的信息称为完美信息，即完美信息下各个决策结不会混同。

不完美信息是指完美信息的逻辑逆。在不完美信息下，后行动者不能判断几个决策结中具体是哪一个，几个决策结都有可能。在猜硬币游戏中，你有信息可能判断出盖住正面的可能性是0.8，反面是0.2，这也是不完美信息。尽管左边决策的可能性大，但不能排除是右边的决策结。即使你有信息能知道左边决策结的可能性是0.9，仍然是不完美信息。所以同样是不完美信息，信息的含量可能有很大的差异，不完美信息只是排除完美的情况。信息的形式可以千差万别，然而，形式不同的信息，可能在结果的作用上是等效的。我们用信息作用后果来标记信息，而忽略信息的具体特征。

例如：“盖硬币的人是把硬币抛出去就捂住的”与“他是在扑克牌中抽一张，抽到红牌正面朝上，黑牌反面朝上”。这两种信息尽管形式不同，但两种信息反映的结果是相同的，都表示0.5的概率正面朝上。在博弈分析中，我们不去关注信息的形式，信息导致的后果相同就认为是同样的信息。信息落实到博弈中，就是关于决策结是什么的描述。完美信息是指决策结是单一结的情况，不完美信息就是决策结不是单结。在一组信息下，决策结的某个集合中每一个结都有可能是行动的后果的决策结集合称为信息集。

一般地，在博弈树中，某种信息条件下都有可能的决策结用一条虚线相连，以示在给定信息下这些决策结都有可能。用虚线连接的决策结，表示属于同一个信息集。

二、不完全信息与不完美信息

不完全信息是指自然首先选择，并且至少有一个参与人不知道自然的确切选择。因此，不完全信息动态博弈在博弈树中，起点是自然的选择，而至少有一人不知道自然选择的假设意味着，自然下的决策结至少对一个参与人是不能确切肯定的。因而，不完全信息必然是不完美信息。然而不完美信息可能由先行动的参与人的行为不可观察造成，因此，不完美信息不能等同于不完全信息，即不完全信息是一类不完美信息。

在信息结构的定义中，不完美与不完全是从不同的角度出发的，分别是相对于完美与完全来描述的，然而不完全与不完美信息在一定程度上的联系，又使得在某些情况下不必考虑它们的差异。(www.xing528.com)

不完全信息，强调了自然首先选择，并且至少有一个参与人不知道自然选择的结果。前面已指出过不完全信息的多种形态。现在的博弈模型中，不完全信息主要是指自然首先选择参与人类型，而且参与人自己知道自己的真实类型，其他参与人不能确切知道，但有关于参与人类型的概率分布的公共知识。后面讨论不完全信息主要针对这种情况。在这种情况下，实际上是各个参与人对自然选择的信息了解具有不对称性。

自然首先选择的信息对参与人是对称的情况，不必把它当成不完全信息，可以进行等效简化处理。这种情况可以理解为确定类型的参与人在不确定的环境下的博弈，自然选择了博弈的环境。假如具有了各种环境类型的概率分布信息，这时可用期望收益代替各种战略组合下的收益来处理。因此逻辑上可以把自然的选择放在各个参与人的选择之后，而不影响分析结果。这样做的目的是把自然的选择尽可能简化，以避免不必要的复杂性。换句话说，如果建模过程能够避免的不完全信息应尽量避免。

例如在双寡头产量博弈的分析中，如果参与人1与参与人2的收益函数是：

π1＝（a（θ）－q1－q2）q1－c1q1

π2＝（a（θ）－q1－q2）q2－c2q2

其中q1，q2是产量，假如c1，c2是常数，而a（θ）是随机变量θ的函数，这时没有必要认为是自然首先选择下的不完全信息博弈，无论参与人的行动是否有先后，定义：

Eπ1＝（E（a（θ））－q1－q2）q1－c1q1

Eπ2＝（E（a（θ））－q1－q2）q2－c2q2

其中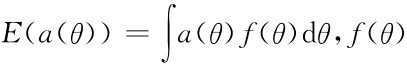是θ的分布函数，就可以把自然的不确定性吸收掉。

当然，我们前面的分析中如果假定ci是参与人自己知道而对方不知道的情况，这时我们就不可避免地需面对不完全信息的分析。

在后面的论述中，我们讲的不完全信息，都是指自然选择的后果对参与人具有不对称性的形式。