贝叶斯博弈与混合战略均衡的联系

本节我们来讨论贝叶斯博弈与完全信息静态博弈中的混合策略之间的联系，为此先分析一个简单的博弈，抓钱的游戏，如表4.6。

表4.6 抓钱游戏

抓钱游戏可从这一背景来理解，在桌上放一元钱，两人同时去抓，则每人罚一元，都不抓，不失也不得。若只有一人去抓，抓的人得到那一元钱，不抓的人不得不失，要求同时行动。

对这一问题，纯策略纳什均衡是（抓，不抓）及（不抓，抓）。但存在混合策略纳什均衡，以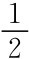的概率选择抓，以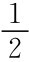的概率选择不抓是纳什均衡。

对参与人2以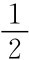的概率选择抓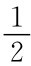，的概率选择不抓能否理解为参与人2有两个类型，一个类型选择抓是最优策略，另一个类型选择不抓是最优策略。如果参与人2也同样思考，这样可以讨论混合策略与贝叶斯静态的博弈的关系。

为此，我们引入参与人的类型，可以理解为好胜心的强度，如果他选择去抓而得到一元钱，则他认为收益比一元钱大，好胜心弱可以理解为抓到一元钱，他认为收益比一元钱少，设参与人1的类型θ1在［－ε，＋ε］内均匀分布，参与人2的类型θ2在［－ε，＋ε］内均匀分布，θ1，θ2独立，用θi来修正抓到钱的收益，如表4.7。

表4.7 贝叶斯抓钱游戏

表4.7表示了θ1型的参与人1与θ2型的参与人2博弈时的收益。这是一个不完全信息静态博弈。

下面来分析它的贝叶斯纳什均衡。

纳什均衡策略应满足，若θ21＞θ11，而θ11的均衡策略是抓，则θ21的均衡策略也是抓，若θ21的最优策略是不抓，则θ11的最优策略也是不抓，即有一分界点θ＊1，当θ1＞θ＊1时抓是最优的，当θ1＜θ＊1时不抓是最优的，但不知θ＊1的大小，同理对参与人2，也有分界点θ＊2。

参与人1为θ1类型而选择抓时，参与人2以最优策略应对时

参与人1为θ1类型而选择不抓时，参与人2以最优策略应对时

U1（不抓，θ1）＝0

则θ1型参与人1的期望收益为：(www.xing528.com)

这里是参与人2选择抓的概率，它由均匀分布得到：

当θ1＞θ＊1时，抓是最优的，因此，应该成立。

当θ1＜θ＊1时，不抓是最优的，所以选择抓的收益比不抓多，因此应该成立

整理后得

由此可得：

由于博弈是对称的，θ＊1＝θ＊2可满足，这意味着上式成立时有θ＊1＝θ＊2＝0，这表明，对参与人1，当θ1＞0时选择抓，θ1＜0时不抓，参与人2在θ2＞0时抓，θ2＜0时不抓是贝叶斯纳什均衡策略组合。对参与人1，可以理解为参与人2以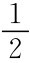的概率选择抓，以的概率选择不抓，相当于对手选择混合策略。参与人2也可同样理解。整体上相当于选择混合策略的博弈。

如果ε很小，可以认为，表4.7的博弈与表4.6的博弈差异会很小，可以把表4.6的博弈作为表4.7的博弈在ε→0时的极限。

实际上，不完全信息静态博弈，在类型间的差异很少时，几乎就是一个完全信息静态博弈，而相应的贝叶斯纳什均衡，在类型间的差异很小时，相当于一个混合策略。

混合策略均衡，直观地理解为随机选择机制，应该说也是好理解的，但也有人对抛硬币式的行动选择不是很满意。上面的例子提供了理解混合策略的思路，而面临参与人类型的不确定，对手施出不同的战略是由于类型决定的，看到的都是对手的不确定战略，但解释却不同。从贝叶斯静态均衡中的解释是对手由于不同的类型，选择不同的最优策略。而对手又是随机确定的，所以表现为策略的随机性，在类型弱化时，博弈趋向于一个完全信息静态博弈，均衡相当于一个混合策略。

一般地贝叶斯静态博弈与完全信息静态博弈之间的联系由纯化定理给出，它通过对策略组合的偏好来引入参与人类型，参与人的类型由k维向量定义，k是战略组合数，这k维向量的各分量独立且服从［－1，＋1］的均匀分布，每一策略组合与一个分量相对应，用此分量修正参与人战略组合下的收益，这样可以把支付函数与类型的联系定义为：

u˜i（s，θi）＝ui（s）＋εθsi

这样引入了一个贝叶斯静态博弈，如果策略组合编号为1，2，…，k，则参与人i的类型是（θ′i，…，θki）。与效用函数的联系相当于引入了一个随机波动修正原理的收益。而ε的大小反映了类型差异的大小，ε→0时，就等效于原来的博弈，但ε≠0时，它是不完全信息静态博弈，可以求得与ε有关的贝叶斯纳什均衡。所求的贝叶斯纳什均衡在ε→0时相当于混合策略。