不完全信息与海萨尼转换的介绍

不完全信息是完全信息的逻辑逆，是指至少有一个参与人不知道自然初始选择的行动。不完全信息实质上就是博弈结构中本身就带有不确定性的博弈类型。

依据对自然选择信息的了解程度进行分类，一个极端是完全信息，另一个极端是没有自然选择的信息。完全信息我们已经会处理，而没有信息，任何人也无从处理。因此在这两个极端之间的不完全信息，一方面是指有一部分信息，另一方面是指又不具有能确定博弈结构的足够信息。这里肯定还存在对不完全信息的类型区分。下面指出几种可能的不完全信息。

1）参与人知道自然的选择是一个随机变量，并且其分布函数是公共知识；

2）参与人知道自然的选择是随机的，但分布函数不是公共知识；

3）参与人知道自然的选择不会出现唯一的结果。但到底有些什么结果不清楚，也许对一些状态有一些了解；

4）参与人只知道自然选择是不确定的，此外别无所知。

例如，基于一项全新技术的新功能产品，把市场对产品反应当作自然选择的状态。即使可以说出市场需求的类型，但很难有市场类型的概率分布知识。

既然不完全信息是多种形态的，可以肯定有许多不完全信息是目前尚未形成分析与研究方法的。在经典博弈中，实际上只能处理靠近完全信息的那类不完全信息模型。这就是要强调，通常所说的不完全信息静态博弈只是对一类不完全信息的处理方法。许多不完全信息处理方法都有待开发。

在经典博弈论中已经形成共识，并已有公认分析方法的不完全信息是指如下定义的不完全信息：自然的首先选择是一个关于参与人类型的随机变量，并且它的分布函数是参与人的共同知识。对这种不完全信息，给出条件：自然选择已知时，就意味着成为一个完全信息问题。不同的选择意味着一系列完全信息问题。当然参与人是不变的，行动集也是不变的。

作为一种处理技巧，可以把自然首先选择的随机信息加到参与人的支付函数上，即参与人的收支函数是在众多收益函数中摇号出来的。同样也可以理解成参与人类型的随机性。

在实际例子中，上面的论述理解起来很直观。比如企业竞争，你不知道对手的成本函数。你可以理解“自然”在许多有确定成本函数的对手中摇号选出了一个对手在你的面前与你博弈。

用市场进入博弈来更具体地说明。参与人1是在位者，参与人2是进入者。如果参与人2不知道在位者的成本。如果完全不知道根本无法分析。如果知道单位产品成本在区间［1，2］内，但不知道分布是什么还是难以分析。如果知道单位产品的成本只有1或2两种情况，而进入者的单位产品成本为2是公共知识，则可以描述成2个带有条件的完全信息静态博弈，假如两种成本下的收益如表4.1，其中假设低成本在位者面对高成本进入者时，斗争比默许收益更大。

表4.1 不完全信息市场进入

一种自然的思路是：如果在位者成本是2，可以求出纳什均衡是（默许，进入），如果在位者的成本是1，纳什均衡是（斗争，不进入）。进入者可能会这样想，如果在位者是高成本就进入，如果是低成本就不进入。如果你知道高成本与低成本的可能性大小，就可以用期望收益来权衡。

如果在位者高成本的概率是p，进入遇到高成本在位者的收益是40，而遇到低成本在位者的收益是－10，则进入的收益是40p＋（－10）（1－p），不进入的收益是0，这样就可以进行决策了，只要比较40p＋（－10）（1－p）与零的大小就能决定是否进入。

在1967年以前，对不完全信息的博弈尚未找到处理方法，对现在普遍认同的不完全信息处理的规范方法由海萨尼提出。

海萨尼引入了一个海萨尼转换，主要思路是引入一个虚拟的参与人“自然”。博弃的各个参与人分别在自然管理的不同房间内，同一房间内的参与人具有不同的类型，是某一编号参与人的候选人。比如参与人1在一个房间内，而在参与人1所在的房间内有多个人，各个参与人都有与自己的类型相关的收益函数，并且编了号。自然采用随机规则选出一个作为参与人i，让这个参与人来参加博弈。这个参与人自己知道自己的收益函数，自然也采用随机的方式选择其它参与人，所以参与人i不知道其他人的收益函数，但自然公布了随机选择的规则，参加博弈的参与人具有了自然对参与人进行随机选择的公共知识。

如在表4.1的例子中，参与人1是两个类型的两人在一个房间中，自然以概率p选择高成本的参与人1，即在位者。而进入者参与人2的房间中只有一人。(www.xing528.com)

我们用Θi表示参与人i的类型集合，θi∈Θi表示一个具体的类型，则θ＝（θ1， θ2，…，θn）就是表明n个参与人类型的向量。自然的随机规则是赋予这一向量一个概率P（θ1，θ2，…，θn）或概率密度f（θ1，θ2，…，θn），即自然在Θ1×Θ2×…×Θn＝Θ中定义了概率，并且把这一知识扩散成公共知识。这样，n个参与人带着关于类型的分布知识及自己的具体类型的信息进行博弈。如果强调不完全信息静态博弈，就是n个参与人同时选择行动的博弈。当然作为一个博弈，其它的必须因素如战略空间与收益函数是必须要有的。

理论上说，对参与人i，可以有自己的类型依存的战略空间，记为Ai（θi），即不同类型的参与人i有不同的策略空间。为使描述简洁，我们假定各种类型的参与人i的策略空间是共同的，即与类型无关。表面上看这似乎是缩小了考虑的范围。但定义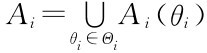时，Ai（θi）⊂Ai把Ai作为各种类型参与人i的共同策略空间，并不会产生本质差异，后面我们都假定战略空间与类型无依存性。

对收益函数，一般的描述是一个定义在A×Θ中的函数，A＝（A1，A2，…，An），参与人i的收益函数是ui＝ui（a1，a2，…，an，θ1，θ2，…，θn），ai∈Ai，，θi∈Θi，即收益函数既与策略组合又与类型组合相关。如在表4.1所示的例中，进入者的收益函数与策略组合有关，也与在位者的类型有关。

由于假设参与人i知道自己的确切类型，这种参与人i的私人知识对了解其他参与人的类型是否有作用呢？这要看自然给出的随机规则的形式。如果自然对各个参与人按独立规则选择，这时P（θ1，θ2，…，θn）＝P1（θ1）×P2（θ2）×…×Pn（θn），其中Pi（θi）是i参与人属于θi的类型的概率。显然在这种情况下，参与人i知道的自己类型的私人信息无助于判断其他参与人的类型。一般地，在各参与人类型分布不独立时，可用条件概率来修正参与人类型地概率分布。用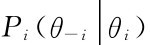表示参与人i知道自己的类型，知道自然选择的P（θ1，θ2，…，θn）时对其他参与人类型分布的概率。依据条件概率公式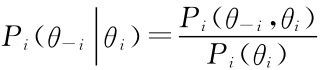，今后我们都假定各参与人的类型是独立的。

上面论述中实际上是以离散型随机变量为基础的，许多时候，类型可能是一个连续型随机变量。如在表4.1所表述的博弈中，在位者的成本如果服从［1，2］的均匀分布，这时需用密度函数。更复杂的情况可用概率测度描述。为了不分散注意力，下面在理论分析时，只对离散型的情况进行论述，而相应的内容扩大到连续型随机变量并不困难。

把上面的描述总结成不完全信息静态博弈的定义。注意，再次强调用海萨尼转换的不完全信息是一种类型的不完全信息，并非全部类型的不完全信息。也可以称为海萨尼不完全信息。以海萨尼不完全信息为基础的n人静态博弈，一般称为n人静态贝叶斯博弈。

定义4.1.1 n人静态贝叶斯博弈的战略式表述是指：n个参与人，每一个参与人有不同的类型，以Θi表示参与人i的类型的集合，θi表示参与人i具体的类型。Ai表示参与人i的策略空间，参与人i知道自己的类型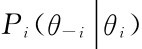，是参与人i关于其他参与人的类型的概率分布知识，n人同时选择策略，收益函数为ui（ai， a－i，θi，θ－i）。

我们用G＝（A1，A2，…，An；θ1，θ2，…，θn；P1，P2，…，Pn；u1，u2，…，un）代表这个博弈。简记为G＝（A；Θ；P；u）。

有一种自然首先选择需要注意一下，它可以不用海萨尼转换进行描述。尽管自然的选择影响参与人的收益函数，但它以一个共同的随机变量影响参与人的收益函数。它不能描述成参与人自己知道的类型。这种情况可以当成自然进行最后选择的风险博弈来处理。

为此我们分析下面的例子，如表4.2，两房地开发企业面临着竞争，都可以在某一城市小区投入开发，也可以不开发。收益受市场需求的影响。市场需求有高与低两种结果，高需求的可能性是P，低需求的可能性是（1－P）。

表4.2 需求风险的企业竞争

市场的需求可以认为是自然按（p，（1－p））的随机发生器选择需求的高与低。我们可以认为先有自然选择了市场，后再是二个开发商同时行动。实际上，可以理解成二个开发商同时选择行动，再由自然选择市场需求。这是一个随机收益的博弈分析，这两种理解本质上没有差异。但这一博弈按自然先选择的方式来理解，虽然很像贝叶斯静态博弈，但却不是贝叶斯静态博弈。因为如果非要通过参与人的类型来描述，等价于自然按共同随机规则选择各个参与人。比如自然摇号，摇到1表示参与人1与参与人2都是1型的；摇到2表示两人都是2型的。1型对应于高需求收益，2型对应低需求收益。这样，由于假设参与人知道自己的类型，则立即就可以推得另一参与人的类型。因而失去了自然随机选择不确定性的信息。所以，它与参与人自己知道自己的类型是不相容的。

参与人的类型确定，而博弈环境具有随机性时，可以认为是参与人的收益受一个共同的随机变量影响，即收益u1（a1，a2，θ）与u2（a1，a2，θ），θ是同一个随机变量。处理这种情况比较方便的方法是把自然的选择当成最后的选择，作为风险来处理。如果把随机收益改用期望收益替代，就是一个完全信息的静态博弈。

对表4.2的博弈，如两家都选择开发时，参与人1的收益是4p－3×（1－p）＝7p－3同样地可以计算出其它的期望收益。如表4.3。

表4.3 市场不确定企业竞争等效博弈

引入了自然作为参与人，n人静态贝叶斯博弈实际上是n＋1人的动态博弈，第一阶段是自然先行动，选择参与人的类型。第二阶段是n个参与人同时行动。当然自然的收益不需要定义。他没有对某种局面的偏好。如果非要定义自然的收益，则可以理解为自然在任何情况下的收益均为0。