逆向归纳法与参与人的理性介绍

我们一直都是假定参与人是理性的，并且“每个参与人是理性的”是博弈的参与人的共同知识。在这一要求下，用逆向归纳法求出的解是可以接受的，并且显得直观。但是，存在许多因素使要求的理性得不到满足的情况。因此，子博弈精炼纳什均衡是否为过于理想化的均衡呢？这是一个仍然值得探讨的问题，我们介绍下面的两个例子，以启发读者的思考。

图3.10表示一个有n个参与人的博弈，每人行动一次，每个人的行动是R与T的二选一，每一参与人若选T，则博弈就结束，后面的人不再有选行动机会，若参与人i选R，则博弈继续由参与人i＋1选择，收益如图。

图3.10 说明逆向归纳法困境的博弈

参与人1先行动，若参与人i选了T，则每个人的收益是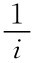，若每一个参与人都选了R，则每人的收益为2，按逆向归纳法来分析，每个参与人的策略“若有机会行动就选R”是子博弈精炼纳什均衡，均衡路径是R出现了n次的路径。

考虑不同的n对参与人行动的影响，为此只要考虑不同的n对第一个参与人的想法的影响，参与人的收益是共同知识的假设，可信吗？可能很多人会考虑万一某个人选T时，我们就不能得到2的收益，也许有了这种想法，第一参与人可能会把他选择T的收益抬高。n越大这种想法越强烈，这种想法实际上把博弈的结果与博弈的结构都作为参与人的收益的有机组成部分，事实上是对外生收益函数这一假设的挑战。事实上绝对理性的任何弱化都会对外生的效用函数提出疑问，这是值得进一步探讨的问题。另一方面，即使收益函数是公共知识，也许还有犯错误的可能性。如果每个人选择R的概率很大，但所有参与人都选R的概率也会很小。因此会有“何必置于不确定之中”的想法而选择结束博弈。

图3.11代表另一种情况，该博弈被称为蜈蚣博弈，这一博弈也提示了许多值得深思的问题。博弈有两个参与人，每个人有99次选择行动的决策点，两人交替行动，但每个人都可以在决策结上选择T来结束博弈，参与人1在第K次选择T而使博弈结束时，每人的收益是（K，K），选R时博弈由参与人2继续行动，参与人2在第K次选T而结束博弈时，收益为（K－1，K＋2）。参与人2在最后一次选R时，收益为（100，100）。(www.xing528.com)

图3.11 蜈蚣博弈

这一博弈用逆向归纳法进行分析时，可以看到，参与人2进行最后的选择时，选T是最优的，往前递推，参与人1最后一次的最优策略是选T，如此往前推进，可以得到结论：“有机会选择就选T”就是子博弈精炼纳什均衡，因而实际的均衡路径是参与人1在第一次时就选择T，从而使博弈结束。

但是，如果参与人1没有选T而选择了R，作为参与人2认为参与人1是非理性的，还是理性的呢？实际上参与人1在第一次选R，正是合作倾向的体现。逆向归纳法是“没有任何合作动机”的非合作博弈的分析工具，所得到的结果与实际情况有差距。

实际上，上述博弈中作一个小的改变，如果减少一次参与人2的选择机会，最后一次由参与人1选择，若选R，收益为（100，101），用逆向归纳法分析可以得到，“有机会选择就选R”就成为子博弈精炼纳什均衡。与原博弈相比，变动的差异是如此之小，结果却大相径庭。这也是一个十分深刻的问题。同一实际问题博弈模型由不同的人来构造，模型有差异是必然的，很小的模型差异能够保证解的性质也是很小的差异吗？至少，在这一例子中可以看到，情况并不理想。这可以称为结构不稳定问题。