混合策略的介绍，如何来表示这些混合策略呢

一、一般描述

前面我们已经接触过无纳什均衡的博弈，（参看表田忌赛马的例子），实际上许多人为构造的游戏都不存在纳什均衡。否则，游戏将会失去吸引力。然而，这是从纯策略的意义上说的。分析一个简单博弈，两个参与人在进行猜币游戏，一人坐庄，盖住硬币。一人猜正反，如果猜中，猜者获胜，得1元钱，庄家付出1元钱；反之庄家得1元钱，猜者付出1元。

很容易构造出该博弈描述表2.10。

表2.10 猜硬币的游戏

按照前面的纳什均衡定义，该博弈没有纳什均衡。然而游戏者仍然会有稳定的策略。这种策略是使对方抓不住采取什么策略的规律，盖正或反并不重要。可以采用随机思路。也许庄家可以把硬币抛出去，连自己都不知道就盖住。让对方猜，猜者也可用随机猜，也可以用抛硬币，抛出正面猜正面，抛出反面猜反面。直观上这种方法是两个理性人的最优策略。这实际拓广了策略的含义。也就是按预定的可能性机制选择具体策略，按抛硬币的策略进行博弈，这时收益是不确定的，总共四种情况，出现的可能性均为1／4，因此可用数学期望来作为收益，即把庄家的收益理解为一个随机变量。

表2.11 庄家的随机收益

则可用数学期望来衡量庄家的收益

同理，可对猜者作同样的描述。

这实际上是对博弈中策略的一种扩充，也就是在原来给定的策略中，按照一定的随机规律来选择策略。随机选择策略的方式称为混合策略。原来给出的策略称为纯策略，即随机选择纯策略称为混合策略。

在上例中，盖正、盖反是庄家的两个纯策略，而以“1／2的概率盖正，以1／2的概率盖反”是一个混合策略，当然以“1／3的概率盖正，2／3的概率盖反”也是一个混合策略。对纯策略赋不同的概率就得到了不同的混合策略。因此，即使纯策略是两个，混合策略是无穷的。

如何来表示这些混合策略呢？我们可以建立混合策略与向量之间的一一对应关系。如“以1／3的概率盖正，以2／3的概率盖反”可以对应（1／3，2／3），这样（p1， p2）就对应于“以p1的概率盖正，以p2的概率盖反”的混合策略。当然，是概率就要求有p1≥0，p2≥0且p1＋p2＝1。

可以把上面的描述一般化，引出混合策略的概念。

定义2.6.1 在策略博弈G＝｛S1，S2，…，Sn，u1，…，un｝中，假设参与人i有mi个纯策略，si＝｛si1，si2，…，simi｝，pi＝（pi1，…，pimi）（0≤pij≤1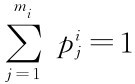，）以pij的概率选择sij纯策略的策略称为混合策略，由于混合策略的本质在于选择纯策略的概率，以后就直接用pi＝（pi1，…，pimi）表示混合策略。

在增加了随机选择策略的思路后，原来的由纯策略组成的策略空间就扩充了，参与人i的策略空间在混合策略的意义下可与mi维欧氏空间中第一象限内满足pi1＋pi2＋…＋pimi＝1的点集相对应。mi为纯策略的个数，而纯策略对应于坐标轴上的点，如策略si1对应于pi＝（1，0，…，0），即纯策略可以看成是混合策略的特例。用pi来表示参与人i的混合策略空间。

每个参与人，都可以在混合策略空间中考虑博弈的策略，当每个参与人选择混合策略后，就形成了混合策略组合。若pi是参与人i的混合策略，记p＝（p1， p2，…，pn）为混合策略组合。用p－i＝（p1，…，pi－1，pi＋1，…，pn）表示参与人i以外的参与人策略组合。

在混合策略的定义下，由于策略的随机性，使得每个参与人的收益具有了随机性，一般地，可采用收益的数学期望来衡量混合策略组合的收益，若p＝（p1， p2，…，pn）是混合策略组合，参与人i的期望支付定义为：

有了这一支付后，纳什均衡可定义为：

定义2.6.2 在策略式博弈G＝｛S1，S2，…，Sn，u1，…，un｝中，若p＊＝（p＊1， p＊2，…，p＊n）是一混合策略组合，对每一个参与人，满足

则称p＊是混合策略纳什均衡，

为了更直观地描述混合策略，下面对猜硬币游戏进行讨论。

在表2.10中，参与人1有两个纯策略，所以混合策略空间为

同理，p2＝｛（p21，p22）｜p21＋p22＝1，p21≥0，p22≥0｝

在混合策略组合（p1，p2）中，参与人1的收益函数为

由于现在只有两个纯策略，因此，p12＝1－p11及p22＝1－p21

可得

E1（p1，p2）＝（2p11－1）（1－2p21）

E2（p1，p2）＝（2p21－1）（1－2p11）

可以验证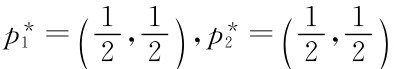是混合策略纳什均衡。

二、混合策略求解

引入混合策略后，策略式博弈都是无限策略的博弈，所以在计算上都可转化为多变量函数求极大值的问题。先从下面的数值例子中开始讨论。

表2.12 说明混合策略的数字例子

显然，可以看到，该博弈没有纯策略的纳什均衡，但存在混合策略纳什均衡，为此设p A为参与人1选纯策略A的概率，p B，p C，p D同样规定。

E1＝2p Ap C＋5×p A×p D＋3×p B×p C＋2×p B×p D

＝（2p C＋5p D）p A＋（3p C＋2p D）×p B

在上式中，（2p C＋5p D）是参与人1采用纯策略A，而参与人2采用（p C，p D）混合策略时参与人1的收益。（3p C＋2p D）是参与人1采用纯策略B，参与人2采用混合策略（p C，p D）时参与人1的收益。所以采用混合策略的收益相当于用纯策略收益按概率的加权平均。同理

E2＝（4p A＋2p B）×p C＋（2×p A＋5×p B）×p D

可用两种思路来求混合策略纳什均衡。

极值法：由纳什均衡的定义。由p B＝1－p A，p D＝1－p C，实际上是一个以p A，p C为变量的极值问题。因此，令

得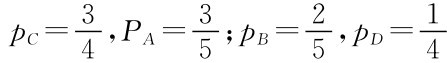

（p A，p B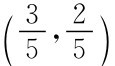）＝；（p C，p D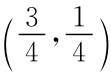）＝可能是纳什均衡，很容易验证它是极大值点，因而是纳什均衡。

均衡法：从E1＝（2p C＋5p D）p A＋（3p C＋2p D）p B中观察，若成立。

2p C＋5p D＞3p C＋2p D

则参与人1的最优策略是p A＝1，p B＝0。反之，p A＝0，p B＝1是最优的。

因而若2p C＋5p D≠3p C＋2p D时，参与人1必然会选择纯策略，所以在没有纯策略纳什均衡时，混合策略纳什均衡的必要条件是

2p C＋5p D＝3p C＋2p D

同理，

4p A＋2p B＝2p A＋5p B

即以混合策略中有可能被选择的纯策略来应对另一方的混合策略时，各纯策略的收益相等。

可由此两式解得：

上述例子中的特点，可以推广到一般情况，

对G＝｛S1，S2，…，Sn，u1，…，un｝。若p＝（p1，p2，…，pn）是一个混合策略组合，则

Ei（pi ，p－i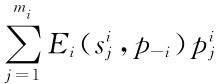）＝j＝，而Ei（sij，p－i）是参与人i选择sij策略，其他人选择p－i时的收益。这一式子表明，选择混合策略纳什均衡的收益可以理解为选择纯策略收益以概率进行加权的平均收益。

考虑均衡法的思路是：如果p＊＝（p＊1，p＊2，…，p＊n）是纳什均衡，且有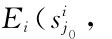 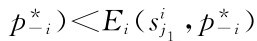成立，那么混合策略纳什均衡中，必然成立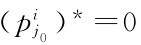。(www.xing528.com)

因为当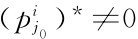时，令：取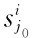的概率为0，取sij1的概率为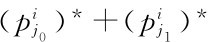，并且保持其它策略的概率不变，就能增加收益。因此，混合策略纳什均衡中取正概率的纯策略必成立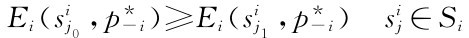

也就是说，混合策略纳什均衡中取正概率纯策略的收益不低于任何纯策略。

进一步的推论是，若混合策略纳什均衡中赋予正概率的纯策略，它们具有相同的收益，即

如果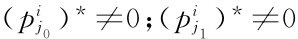，则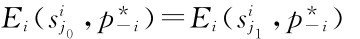

在问题较简单时，就能应用这一规律来求得混合策略纳什均衡，前面例子中均衡法就是这一原理的应用。

对于极值法，我们可以从反应函数来理解，考虑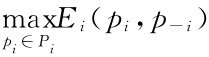，可求得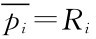 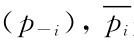是上述最优问题的解。称Ri（p－i）是参与人i的反应函数（不一定是单值函数）。

如果对每一参与人都求出反应函数，可以得到i个反应函数，而混合策略纳什均衡满足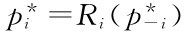 i＝1，2，…，n。

一般地，纳什均衡的求解不能依赖于手工完成。但通过手工计算可以加深理解。而且许多实际应用的分析，手工计算可能还是低成本的，下面再分析两个复杂一点的例子。

表2.13提供了不存在混合策略纳什均衡的例子。

表2.13 不存在混合策略纳什均衡的博弈

显然，（M，R）是唯一的纯策略纳什均衡，下面分几种情况来讨论混合策略纳什均衡，先考虑参与人1取混合策略，参与人2取R是否能成为纳什均衡呢？记p1， p2，p3分别是参与人1取U，M，D的概率。由于

E1（（p1，p2，p3），R）＝0×p1＋3×p2＋1×p3

可知，p1＝p3＝0是纳什均衡的必要条件，因为U，M，D三个纯策略的收益以M为最大，所以，取U，D的概率为零，这实际上是参与人1取M的纯策略，所以参与人2取纯策略R时，只有（M，R）的是纯战略纳什均衡。因此，可能存在的混合策略必然是参与人2在L与R上都有正概率γ1，γ2的混合策略纳什均衡。参与人2的期望效用为：

E2（（p1，p2，p3），（γ1，γ2））＝（p1＋2p2＋3p3）γ1＋（2p1＋3p2＋p3）γ2

由于γ1≠0，γ2≠0的要求，（p1，p2，p3）为参与人1的混合策略纳什均衡时需成立p1＋2p2＋3p3＝2p1＋3p2＋p3。

这实际上是参与人2用L与R应对参与人1的混合策略有相等收益给出的。

即 p1＋p2－2p3＝0

由 p1＋p2＝1－p3

得，p3＝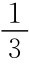

又由 E1（（p1，p2，p3），（γ1，γ2））＝（3γ1）p1＋（3γ2）p2＋（γ1＋γ2）p3

可得 1＝γ1＋γ2≥3γ1，1＝γ1＋γ2≥3γ2

即

这与γ1＋γ2＝1矛盾。

因此，不可能有γ1×γ2≠0的混合策略纳什均衡。

综合得，该问题没有混合策略纳什均衡，（M，R）是唯一纯策略纳什均衡。

对表2.13的博弈作简单改变，考虑表2.14的博弈。

表2.14 多个混合策略纳什均衡的例子

（M，R）仍是唯一的纯策略纳什均衡，但存在着混合策略纳什均衡。考虑

E1（（p1，p2，p3），（γ1，γ2））＝（3γ1＋0×γ2）p1＋（0×γ1＋3γ2）p2＋（2γ1＋2γ2）p3

＝（3γ1）p1＋3（1－γ1）p2＋2p3

E2（（p1，p2，p3），（γ1，γ2））＝（p1＋2p2＋3p3）γ1＋（2p1＋3p2＋p3）γ2

由E1可知，若γ1＞，则3γ1＞3γ2，3γ1＞2，这时p2＝p3＝0才可能是纳什均衡，然而U不是纳什均衡，因此这种情况下不会有混合策略纳什均衡。

同理，若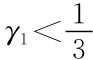及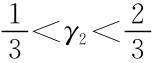，都不会有混合策略纳什均衡。

因此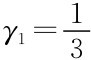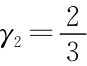，，及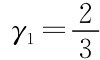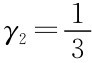，才有可能是纳什均衡。

由γ1≠0，γ2≠0时，p3＝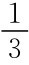

为两组混合策略纳什均衡。

所以该问题有两个混合策略纳什均衡及一个纯策略纳什均衡。

三、反应函数的直观图示

当参与人是两个，且每个参与人只有两个纯策略时，可以用平面坐标清楚地把反应函数及纳什均衡的图示描述出来，下面结合实例来讨论。

在经典的社会福利博弈里，参与人是政府和一个流浪汉。政府有两个策略，救济或不救济。流浪汉也有两个策略，找工作或游荡。很显然，政府希望帮助找工作的流浪汉，但帮助成为流浪汉的预期时，流浪汉可能不愿找工作。

表2.15 社会福利博弈

这是一个不存在纯策略纳什均衡的博弈，下面来考虑混合策略纳什均衡，若政府以p的概率选择救济，（1－p）的概率选择不救济，流浪汉以γ的概率选择找工作，（1－γ）的概率选择游荡。则政府的效用E1，与流浪汉的效用E2，分别为：

E1＝（3γ－（1－γ））p＋（－γ）（1－p）＝（4γ－1）p＋（－γ）（1－p）

E2＝（2p＋（1－p））γ＋3p（1－γ）

当γ给定时，由E1，可求得政府的反应函数p＝R1（γ）

同理：

图2.3直观地反映了R1（γ）与R2（p）。

图2.3 反应函数与纳什均衡

图中R1（γ）与R2（p）的交点是混合策略纳什均衡，p＝0.5，γ＝0.2也就是说政府以12的概率选择救济，而流浪汉是以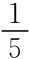的概率选择找工作。

混合策略纳什均衡在一次性的博弈中理解上有一定的困难。尽管混合策略是确定的，但博弈的实际结果却是不确定的，上例中任何策略组合，都有可能是博弈的结局，如果有一系列的这种博弈存在，则从比例上可以体现出混合策略的定义，政府会对50％的流浪汉选择救济，又有20％的流浪汉会选择找工作。

在人为的游戏中，理解混合策略纳什均衡可能是更直观地，一般在学习这一内容时，往往都会从扩大博弈的边界的方向上去思考，如许多人可能希望“证实”流浪汉是什么类型，在游戏中，希望获得对方策略的信息。然而，混合策略是假设没有模型规定以外信息可使用情况下的最优策略。