无限策略博弈分析，库诺特竞争模型

在博弈策略空间是有限时，均衡的计算可以用划线法等直观方法求得，有时直接验证也不困难，然而有时会碰到策略是无限的情况。显然在纳什均衡的定义中，包括无限策略的情况。这时计算就成了问题，本节讨论无限策略的纳什均衡求解问题。

无限策略往往会与策略变量联系起来，以一个实数代表一个策略，且收益函数是策略变量的函数，策略变量的取值范围代表全部策略。这种情况往往可以用微积分作为工具来讨论，在讨论一般模式以前，我们先讨论著名的库诺特寡头竞争模型。

一、库诺特竞争模型

有企业1，企业2两家企业，生产同质产品，供应同一个市场，且没有其他供应商，每家企业的策略是产量；支付是利润。

设q1，q2分别是企业1与企业2的产量，qi∈［0，＋∞），［0，＋∞）是企业的策略空间，当企业1，企业2分别选择q1，q2的产量时，市场的供应量为q1＋q2＝Q，分别的成本为C1（q1）与C2（q2），市场的出清价格为p＝p（q1＋q2）。企业1与企业2的利润为π1（q1，q2），π2（q1，q2），它们的具体表达式如下：

π1（q1，q2）＝q1p（q1＋q2）－C1（q1）

π2（q1，q2）＝q2p（q1＋q2）－C2（q2）

若（q＊1，q＊2）是纳什均衡，由纳什均衡的定义，在p（q1＋q2）与Ci（q）存在导数时，q＊1应满足

同理

上述两个方程可求出满足方程的q＊1与q＊2，当然，如果要验证（q＊1，q＊2）是纳什均衡，须验证下列矩阵是负定的，称为二阶条件，它保证（q＊1，q＊2）是极大值。

为了更好地理解纳什均衡，引入反应函数的概念是方便的，这实际上是划线法求解纳什均衡的推广。

若企业2的产量q2给定，则企业1的产量q1，只有在满足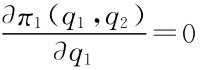时才可能是最优的，其他参与人的策略固定，参与人1的最优产量记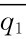＝k1（q2），即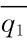是q2固定时企业1的最优产量，称为企业1的反应函数。对企业2同样可以定义反应函数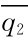＝k2（q1），反应函数在图中是一条曲线。两个参与人的两个反应函数就是图中的两条曲线，如图2.1，根据定义，纳什均衡必在反应曲线的交点上。

图2.1 反应函数与纳什均衡

反应函数交点是否为纳什均衡需作二阶条件验证，如有多个交点且二阶条件成立，则就说明有多个纳什均衡。

如果以具体的函数来讨论库诺特模型，可以得到确定的结果，设C1（q）＝C2（q）＝qc，其中c为正常数，且p（q1＋q2）＝a－（q1＋q2），a为正常数。

则收益函数π1（q1，q2），π2（q1，q2）的形式为

π1（q1，q2）＝q1（a－q1－q2）－cq1

π2（q1，q2）＝q2（a－q1－q2）－cq2

企业1的反应函数由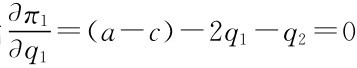得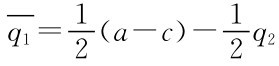

同理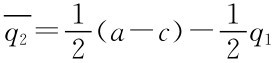

这两个方程决定的曲线交点由

可解得

在纳什均衡下，企业1与企业2的利润为分别是：

通常，博弈分析会应用于比较不同博弈结构下参与人行为的结果，就上例而言，可以考虑寡头竞争下的市场供给、企业利润与垄断企业的供给与利润差异。

若市场是垄断的，则可以理解为两家企业合并为一家企业，Q是产量，则

π（Q）＝Q（a－Q）－cQ

由(www.xing528.com)

利润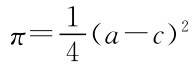

由此可以比较得到：

即垄断可以比寡头竞争获得更多的利润，而垄断会降低市场的供应量。

二、连续策略的一般描述

若n个参与人的博弈，参与人i的策略空间为Ai，xi∈Ai代表一个策略，收益函数ui＝（x1，x2，…，xn），其纳什均衡x＊＝（x＊1，x＊2，…，x＊n）定义为≥，xi∈Ai；i＝1，2，…，n。

当Ai为实数区间，且效用函数为可微函数时，可用求极值的方法求解纳什均衡，根据定义，若x＊为纳什均衡，则x＊满足：

这使得计算纳什均衡的过程直观，方便。

对参与人i的反应函数，一般地定义为其他人策略不变时参与人i的最优策略。即如果Ri（x－i）是参与人i的反应函数，则ui（Ri（x－i），x－i）≥ui（xi，x－i）成立。

在ui可微时，反应函数由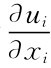＝0，i＝1，2，…，n决定。当然ui的形态较复杂时，可能会出现Ri（x－i）不连续、多值等情况，甚至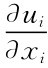＝0的解未必是最优策略。但这些细节处理并不困难，不再在此细究。

若在一个博弈中纳什均衡存在，记x＊＝（x＊1，x＊2，…，x＊n）为纳什均衡，则它必满足：

或

因此，可通过求解上述n个联立方程来求得纳什均衡。

三、无限个纳什均衡的例子

两人分1 000克蛋糕，规则是每个参与人各写出自己要求的数量，交仲裁人，若两人要求数量总和不超过1 000克，每人可获得自己要求的数量，若两人的要求数量超过1 000克，则每人都将一无所获。

这是一个两人博弈，每个参与人的策略空间都是A＝［0，1 000］，实际含义是参与人要求分得蛋糕数量的可能范围。若x1，x2∈A分别为两个参与人要求的数量，收益函数可设为：

显然，若x2固定，参与人1的最优要求量是x1＝R1（x2）＝1 000－x2，因为超过这一数量时一无所获，而小于这一数量时，还有收益增加的机会，同理＝R2（x1）＝1 000－x1。这两个反应函数的图像上是重复的图形x1＋x2＝1 000。不难验证，满足x1＋x2＝1 000的所有解都是纳什均衡，这里我们见到了一个博弈有无穷个纳什均衡的情况。

下面对该问题作一些简单的推广。

若两个参与人都知道，参与人1对蛋糕更加偏爱，则可改变效用函数来反应这一情况，则可设：

其中k＞1，用于描述参与人1对蛋糕的偏爱，k越大，表明他的偏爱更强烈。当然，其他形式的收益函数也可用于更强的偏爱。仍然可以求得x1＋x2＝1 000的解都是纳什均衡，但各个纳什均衡的总效用是

这时，各个纳什均衡的总效用不同，但没有一个帕累托占优的纳什均衡。

若设效用函数是如下的形式：

α＞1表示参与人1爱好风险，0＜α＜1表示参与人厌恶风险。虽然x1＋x2＝1 000仍然都是纳什均均衡，由

可以看到总效应如图示情况：

图2.2 不同α的总效应

这表明，如果与厌恶风险的参与人博弈，会存在总效应最大化的且每人却都有所得的均衡，然而一个喜欢风险的参与对手，总效用最大化只能由一人获得全部。显然不同情况下协调的难度将不同。

这一例子表明，效用函数的不同形式在博弈分析中的差异，说明效用函数设计是博弈论应用的重要环节。