基于有序信息集结与数字图书馆评价的理论和方法

第五节　基于有序信息集结的高校图书馆效率评价方法

图书馆的评价是一个价值判断过程，它是根据图书馆的办馆目标和有关标准，通过对图书馆工作进行系统的调查，做出客观、公正、合理的全面评价。^［86］一般来说，构成图书馆评价问题的要素包括三个：一是被评价对象，也称为评价的客体，即参与评价的图书馆。二是评价的指标体系。它是由不同侧面反映图书馆运行情况的指标构成。三是指标的权重系数。在图书馆的评价中，指标的权重系数是反映各个指标的相对重要性程度。目前对于图书馆的评价有一些定量化评价方法。张爱丽等^［86］将支持向量机（SVM）中的核方法用于高校图书馆效率的分析研究。但是该方法存在一些缺陷：一是常用的核函数有多种，如多项式核、高斯（径向基函数）核、二层神经网络核等，因此在评价中如何选择合适的核函数存在一定的困难；二是核函数评价方法抽取指标的实际意义不是很明确；三是核函数评价方法的计算复杂，同时评价结果也有偏差。基于上述考虑，本节引入近年来发展起来的有序信息集结算子，^{［53］［87］}探讨其在高校图书馆多指标效率评价方面的应用研究。

一、有序信息集结算子的概念

高校图书馆多指标效率评价的实质是一种信息的有效集成。也就是说，我们把各个高校图书馆作为的评价对象，根据它们运行的多个指标所提供的大量信息，按照某种评价准则研究如何集成这些信息并进行评价对象排序，从而确定各个高校图书馆管理效率的高低。

美国著名学者Yager提出了有序加权平均算子^{［53］［87］}（Ordered Weighted Averaging Operator）。有序加权平均算子是介于最大算子与最小算子之间的一种信息集成方法，常规的加权算术平均算子是他们的特例。近年来，有关该算子的理论研究已引起专家学者的关注，它成为国内外十分活跃的研究课题之一，并广泛应用于决策分析^{［87］［88］}等领域。目前国内尚未见到在图书馆领域的应用报道。本节就此作出一些探讨性研究。

先介绍两个概念：

定义7.5.1^［31］　令函数

WA A（a₁，a₂，…，a_n）＝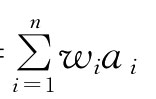

其中W＝（W₁，W₂，…，W_n）是加权向量，满足0≤W_i≤1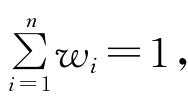则称函数WAA为加权算术平均集结算子。

定义7.5.2^［31］　令函数

OWA（a₁，a₂，…，a_n）＝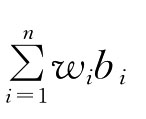

其中b_i是（a₁，a₂，…，a_n）按从大到小的顺序排列的第i大的数，W＝（W₁，W₂，…，W_n）是与OWA相关联的加权向量，满足0≤W_i≤1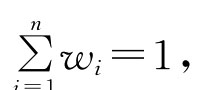，则称函数OW A为有序加权算术平均集结算子。

定义7.5.2表明OWA算子是对n个数a₁，a₂，…，a_n按从大到小的顺序排序后进行有序加权平均的，权系数W_i与数a_i无关，而是与a₁，a₂，…，a_n的按从大到小降序排列的第i个位置的数b_i有关。

特别地，有以下情况成立：

①当W＝（1，0，…，0）^T时，有序加权算术平均集结算子OWA简化成最大化集结算子。

②当W＝（0，0，…，1）^T时，有序加权算术平均集结算子OWA简化成最小化集结算子。

③当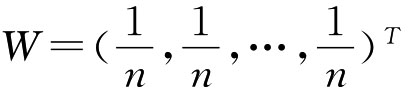时，有序加权算术平均集结算子OWA简化成简单算术平均集结算子。

④当（a₁，a₂，…，a_n）本身就是按从大到小的顺序排列时，此时有序加权算术平均集结算子OWA简化成加权算术平均集结算子。

可见有序加权算术平均集结算子是一类较为广泛的信息集结算子。

定义7.5.2中的权向量W＝（W₁，W₂，…，W_n）^T是可由模糊语义量化算子［53］Q来确定的，即：

其中的Q（x）由下面的分段函数给出：

式中参数0≤a，b，x≤1，对应于模糊语义量化准则的“大多数”、“至少半数”、“尽可能多”的算子Q的参数对（a，b）分别为

（0.3，0.8），（0，0.5），（0.5，1）

二、基于有序信息集结的高校图书馆效率评价模型

设有m个高校图书馆参与评价，记高校图书馆评价对象集表示为S＝｛S₁，S₂，…，Sm｝；设有评价指标集表示为P＝｛P₁，P₂，…，P_n｝，第i个高校图书馆S_i对第j个指标P_j的指标值记为a_ij，i＝1，2，…，m，j＝1，2，…，n，矩阵A＝（a_ij）_m×n称为评价矩阵。通常，指标可分为效益型、成本型。所谓效益型指标是指指标值愈大愈好的指标，成本型指标是指指标值愈小愈好的指标。由于不同的指标往往具有不同的量纲和量纲单位，为了消除它们带来的不可度量性，在决策之前首先应将指标指标作无量纲化处理。然而，决策指标类型不同，无量纲化处理方法也将不同。对于效益型指标，一般可令：

对于成本型指标，一般令：

式中

a^max_j＝Max｛a_1j，a_2j，…，a_mj｝，a^min_j＝Min｛a_1j，a_2j，…，a_mj｝，

即a^min_j，a^max_j分别为第j个指标P_j的最大值和最小值。

显然，b_ij∈［0，1］，i＝1，2，…，m，j＝1，2，…，n。

上述的无量纲化处理的矩阵R＝（r_ij）_m×n称为规范化的决策矩阵，r_ij表示第i个高校图书馆S_i对第j个指标P_j的规范化指标值。显然b_ij愈大愈好。

综上所述，基于有序信息集结的高校图书馆效率评价的计算步骤为：(www.xing528.com)

第一步：由高校图书馆评价矩阵A＝（a_ij）_m×n，计算规范化指标的评价矩阵B＝（b_ij）_m×n。

第二步：计算有序加权算术平均OWA算子相关联的加权向量

W＝（W₁，W₂，…，W_n）。

第三步：采用有序加权算术平均OW A算子对各个高校图书馆指标信息进行有效集成，计算各个高校图书馆的效率的综合评价值，即：

z_i＝OWA（r_i1，r_i2，…，r_in）＝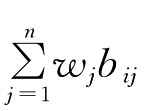

其中b_ij是r_i1，r_i2，…，r_in按从大到小的顺序排列的第j大的数，z_i表示第i个高校图书馆的效率的综合评价值。

第四步：根据计算的各个高校图书馆的效率的综合评价值z_i进行排序。

三、高校图书馆综合评价实例

本节采用《高校图书馆效率的核评价方法》^［86］的例子作实例分析。这里有12所中等规模的图书馆的统计资料。在确定评价指标时，选取较能反映出高等学校图书馆建设的重要指标：校拨总经费（万元）、图书费用（万元）、全馆总人数（人）、馆舍建筑面积（平方米）、总藏书量（万册）、读者人数（人）。具体的指标值如“表7.5.1”所示：

表7.5.1　高校图书馆评价指标

高校图书馆效率评价的计算步骤为：第一步：“表7.5.1”的数据均为效益型指标，指标值愈大表示高校图

书馆规模愈大。计算规范化指标的评价矩阵：

第二步：计算6个指标的有序加权算术平均OWA算子相关联的加权向量：

W＝（W₁，W₂，…，W6）＝（0 0.066667 0.33333 0.33333 0.26667 0）

第三步：采用有序加权算术平均OW A算子对12所高校图书馆指标信息进行有效集成，计算各个高校图书馆的效率的综合评价值，即：

z₁＝OWA（r₁₁，r₁₂，…，r₁₆）＝0×0.9301＋0.066667×0.9167＋0.33333×0.6760＋0.33333×0.6374＋0.26667×0.2442＋0×0.1762＝0.56403同理计算得：

z₂＝OWA（r₂₁，r₂₂，…，r₂₆）＝0.50473

z₃＝OWA（r₃₁，r₃₂，…，r₃₆）＝0.70598

z₄＝OWA（r₄₁，r₄₂，…，r₄₆）＝0.81941

z₅＝OWA（r₅₁，r₅₂，…，r₅₆）＝0.42882

z₆＝OWA（r₆₁，r₆₂，…，r₆₆）＝0.55981

z₇＝OWA（r₇₁，r₇₂，…，r₇₆）＝0.45717

z₈＝OWA（r₈₁，r₈₂，…，r₈₆）＝0.47437

z₉＝OWA（r₉₁，r₉₂，…，r₉₆）＝0.58659

z₁0＝OWA（r₁₀₁，r₁₀₂，…，r₁₀₆）＝0.45641

z₁1＝OWA（r₁₁₁，r₁₁₂，…，r₁₁₆）＝0.33236

z₁2＝OWA（r₁₂₁，r₁₂₂，…，r₁₂₆）＝0.72277

第四步：根据计算的综合评价值得各个高校图书馆的效率从高到低依次排序的结果如下：

高校4＞高校12＞高校3＞高校9＞高校1＞高校6＞高校2＞高校8＞高校7＞高校10＞高校5＞高校11

可见本节的排序的结果和张爱丽等^［86］人的研究差别较大，其研究结果是把高校9和高校11分别排列在第一位和第二位，显然这个结论不尽合理。因为尽管高校9的校拨总经费最大，达到499.4万元，但是其馆舍建筑面积最少，且其图书购置经费、读者人数也不最多；类似地，高校11投入较少，馆舍建筑面积较大，但读者人数最少，所以高校9和高校11的软件和硬件管理效率均不高。而本节的排序结果和原始的统计资料比较相符，因此本节提出的在高校图书馆多指标效率评价模型是有效的。