教育收益率和内部回收率的计量方法

第三节　教育收益率和教育内部回收率的计量方法

我们在上一节已提到，教育收益率可分为个人教育收益率和社会教育收益率两种。前者指个人因受教育，提高了劳动生产技能，从而提高了其劳动产出水平和收入水平，这种因受教育而增加的个人收入扣除税收（指增加的个人纯收入），并经贴现后，与贴现后的教育成本之比值，再乘以100％，即是。用公式可表示为

从这一公式可知，个人教育收益和个人教育成本都应该加以贴现。同理，社会教育收益率公式可表示为

汉森（1963）还把个人教育收益解释为“税后收入差别和私人资源成本之间的差额”，而把社会教育收益解释为“税前收入差别和总资源成本之间的差额”^[4]。

在说明“教育内部回收贴现率”的计量方法之前，我们先来看下列假设案例。

假定有一投资项目，在基年时投入500万元，其利益的回收在次年开始，每年的收益总额为100万元，该项目设计使用寿命为10年，并假定在此10年期间内，每年收益总额不变，而且十年后，该项目报废。下面我们分别用10％和16％的贴现率水平，来分析其现值变化情况。

当贴现率指定为10％时，在收益的第一年，100万元的收益额，其基年的现值只有90.91万元；在第二年，100万元的收益要贴现两次，第一次贴现后，其值为90.91万元（即此值实为收益第一年的贴现值），此90.91万元又必须再贴现一次，使之成为基年的现值，则为82.65万无。依此类推，第三年，100万元收益额经三次贴现后，其现值仅为75.14万元；到第十年时，100万元收益的现值仅为38.55万元。见表7－1。

从表7－1中可见，在现值成本为500万元和贴现率水平为10％时，在10年的收益期内，该项目的现值总收益约为614.49万元，此值超过了500万元的现值成本，说明该项目的投资在此贴现率水平上是可行的或划算的，也就是说，该项目有赚头。但是，如果贴现率为16％，在10年收益期内，其现值总收益仅为483.47万元，成本无法回收，说明在此贴现率水平上，该项目的投资是不划算的。

这种方法常被称为“现值收益分析法”。如果某项目的收益总现值超过现值总成本，说明该项目的投资是可行的；反之，则反是。我们也可把此法称为净现值收益分析法，如果净现值收益（即为现值总收益减去现值总成本后的余额）大于零，则这一投资项目有利可图。如该案例中，贴现率为10％时，净现值为114.49万元，说明这种投资是有利可图的。反之，若净现值小于零时，则这一投资项目无利可图，即会出现亏损，如贴现率为16％时，净现值为－16.53万元，说明该项目无利可图。

表7－1　贴现率假定为10％和16％时的现值

另一种分析法就是“内部回收率法”或“内部回收贴现率法”。国内不少学者把它称为“成本—收益分析法”，这是不妥的，因为此法所要分析的，并不是成本和收益问题，而是回收贴现率问题。在上述案例中，我们可知，在贴现率为10％～16％之间，必有一贴现率值能够正好使现值总收益等于现值总成本，即能正好回收现值成本。通过计算，这一贴现率值略低于13％，说明了在此约13％的贴现率水平上，这一投资项目的现值成本能够正好回收起来。因此，我们把这一正好能够回收现值成本的贴现率，称之为“内部回收率”或“内部回收贴现率”。在具体分析时，我们可用某种计量公式，首先计算出此一内部回收贴现率，如果所指定的贴现率（即某一参考贴现率水平）小于这一内部回收贴现率，则说明这一投资项目值得；反之，若所指定的贴现率大于此一内部回收贴现率，说明该投资项目不值得。如在上例中，小于13％的所有贴现率水平上，投资都是值得的，但是，大于13％的贴现率水平上，其投资就不划算了。

应该注意的是，上述“净现值收益分析法”和“内部回收贴现率法”所得的结论，在绝大多数情况下，几乎都是一致的，但可能也有个别例外。如英国学者阿特金森就指出，当收益存在从正值向负值再回到正值的波动趋势时，或者当需要优先实施某些可能的投资项目时，这两种分析法所得结论，可能出现不一致^[5]。

由上例的分析也可说明，“内部回收贴现率”与“收益率”是完全不同的两个概念。因此，把“教育内部回收贴现率”，当成“教育收益率”看待，是多么的粗心大意。

如，在上例中，若贴现率指定为10％时，其收益率为：

R＝（（614.49－500）/500）×100％＝（114.49/500）×100％＝22.898％

若贴现率为16％时，其收益率为：

R＝（（483.47－500）/500）×100％＝（－16.53/500）×100％＝－3.306％

如果贴现率为13％，即为内部回收贴现率值时，其收益率为：

R＝（（500－500）/500）×100％＝（0/500）×100％＝0.0％

从这些数据的对比来看，我想，再粗心的学者也会发现，这几种收益率值与内部回收贴现率值（13％），是根本不同的。迄今，我仍未能明白，这些显而易见的差别，为什么会有这么多学者搞不清楚，甚至一而再，再而三地弄错？

对“个人教育内部回收贴现率”或说“个人教育内部回收率”，可用下列公式计算而得：

首先，计算个人教育投入的现值成本。假设某一级教育第t年的直接成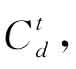本为间接成本为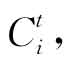，该级教育年限为n年（如大学教育为4年时，n＝4，t则为1—4年），贴现率为r，则对于基年（即，可看成为接受该级教育的前一年）的教育成本现值C_o为

如4年大学教育的教育成本现值为

其次，计算个人教育总收益现值。同样，我们假设只因某一级教育引起的第T年教育收益为I^T（指当年的纯收益，其计算公式下述），贴现率为R，收益年限为N，则对于某一基年来说（同样，我们也可把它看成是接受该级教育的前一年），其收益现值I_o为(www.xing528.com)

在运用和比较上式（7.3.1）和式（7.3.2）时，应特别注意如下两点：

一是两者的时间跨度不同。前一公式的时间t的计算年限仅从1到n，其中n为某级教育学制年数；而后一公式的时间T，严格说来，应从n＋1年开始（假定毕业时间均为每年年底），即从毕业后的下一年开始计算，直到个人退休或死亡为止。由于个人在退休之后，其收入水平也有可能因受某级教育而有所增加，因此，从理论上说，其个人教育收益应该算到死亡之时。但目前在具体操作上，国内外学者均算到退休为止。

二是两者的贴现率可能不同。由于两者的时间跨度不同，其贴现率也不一定会相同。因此，笔者把前者以r代表，后者以R表示。之所以把上面两公式的贴现率，用大小写字母分别表示，正是要让读者明白，不同时期的实际贴现率水平可能是不同的。但是，我们在具体计算内部回收贴现率时，只能假定两者的贴现率一致，即它们没有任何因时间的推移而发生变化，如果无此假定，任何内部回收贴现率都是无从计算的。

由于“教育内部回收贴现率”的概念是，当教育现值总收益等于教育现值总成本（即，教育的现值总成本正好回收起来）时，所计算得到的贴现率水平。据此，它可用下式通过数学中的“迭代法”计算而得，即，令式（7.3.1）和式（7.3.2）的左边相等，并且贴现率均为r

C_o＝I_o

将上式展开，并把R改为r，得

根据式（7.3.3）所计算出来的r值，则为内部回收贴现率，简称内部回收率；N为个人退休或死亡年份；n＋1为某级教育毕业的次年。其他参数的含义同前所述。

举例说明：如4年大学教育的内部回收率，可从下式计算而得

在此，应特别注意：在计算I^T数值时，I^T并不是个人第T年的总收入，而是个人因受到某一级教育而多增加的税后纯收入。具体可用下式计算

I^T＝（某一级教育个人税后年纯收入－前一级教育个人税后年纯收入）

我们在本节和前面两节均已反复说明了，由式（7.3.3）所计算出来的r值，只不过是内部回收贴现率而已，其值的大小，只能用作教育投资优劣以及教育投资可行与否的参评指标，而完全不是一些国内学者所说的“教育收益率”。有些学者甚至把式（7.3.3）说成是计算“教育收益率”的所谓“精确计算法”，这是不对的，应予纠正。

事实上，教育收益率可用下式计算而得

L＝（（I_o－C_o）/C_o）×100％（7.3.4）

其中，

上式中，L代表教育收益率，其他参数的含义如前解释。

从式（7.3.4）可知，如果I_o值足够大，那么，个人的终身教育收益率L值，完全可以超过百分之一百，甚至百分之几百以上的水平，这是完全可能的。而由式（7.3.3）计算出来的内部回收贴现率，一般不会很大（大多在30％以下），而超过100％的水平，是难以想象的。我们从E·科恩（E.Cohn）和杰斯克（T.Geshe）在1979年提供的下列数据，就足以说明这个道理。见表7－2。

表7－2　美国大学和高中毕业生的平均年收入比较

资料来源：E.Cohn ＆ T.Geske，The Economics of Education，Pergamon Press，1990，PP44－45.

从表7－2可见，美国大学毕业生的年收入在23岁之前时，比高中毕业生低，即前者与后者之差为负值。这是因为这些数据是全国平均值，在20—23岁，高中毕业生绝大多数已参加工作，而后来的大学毕业生此时大多正在上大学。但从24岁开始，大学毕业生的年收入超过了高中毕业生，其差额一般随着年龄的增大，有逐渐增大的趋势。到64岁退休时，前者比后者增加约1.7万美元。在整个18—64岁，前者比后者多收入376958美元（我们可暂时把此数据看成为两类毕业生的终身收入差额）。因此，该表数据可说是“年龄—工资—教育水平”曲线的一个典型例子，即教育层次越高，其收入也越高，请参考本书第六章第三节图6－1。

根据赖德胜教授的计算，若间接成本（机会成本）占学生个人教育总成本的50％（舒尔茨认为，机会成本约占个人教育总成本的一半以上），美国1979年的大学生4年所放弃的收入（即机会成本）为43457美元，则4年中的个人教育总成本为86914美元，这一数值只占大学毕业生与高中毕业生终身年收入差额376958美元的四分之一不到，也就是说，美国个人大学教育的投资回报是教育成本的四倍以上。^[6]假如我们在此不考虑其他因素（如不考虑贴现因素），可以认为，在1979年左右，美国个人大学教育的收益率极高，大约为（376958/86914）×100％＝433.71％。

在表7－2中，如果我们把美国人上大学的年龄设定在20—23岁，则美国学生个人受4年大学教育所放弃的机会成本，可认为是高中毕业生在20—23岁的总收入（在此暂不考虑贴现因素），即（13409＋15260＋17385＋16947）＝63001美元。我们在此也同样假定，个人教育的机会成本约占个人教育总成本的50％，则美国在1979年左右，个人受4年大学教育的总成本为126002美元，这一数据也只不过是两类层次毕业生终身收入差额376958美元的三分之一，即个人大学教育的投资回报是成本的三倍。在不考虑贴现等因素时，可以认为，美国在1979年左右，个人大学教育的终身收益率为：（376958/126002）×100％＝299.17％，这或许才是人们追求高层次教育的真正原因所在，也是高层次教育的魅力所在。

科恩和杰斯克的数据，来自美国普查局所调查的1979年不同年龄、不同教育层次的个人统计资料，由于无法预期1979年左右的大学生和高中生在以后几十年的收入变化情况。如果缺乏每一年的不同教育层次的收入数据，我们显然无法用上述式（7.3.3）和式（7.3.4），来计算教育内部回收率r值和教育收益率L值。因为在教育层次相同的情形下，现在的学生在60岁时的收入，显然不可能等同于现为60岁的同教育层次的人的收入。但是，我们完全可以假设，现在的大学毕业生和高中毕业生，在今后几十年内收入的变化速率与上述表格中两者的收入变化速率差不多，也就是说，可以假设今后几十年中，两者收入的增长速度维持上表中的水平，那么，我们就可用上表中的数据对其r值和L值进行计算了。同时，我们也假定美国个人受大学教育的年龄在20—23岁，则，个人在19岁时（即进入大学的前一年），就可以预期他或她上4年大学教育的收益率L值了，同时，也可计算出其内部回收贴现率水平r值。其计算方法仍用数学中的“迭代法”，可根据上述公式，用计算机计算而得，因计算过程非常复杂，在此从略。

以上所述，是计算个人教育收益率和个人教育内部回收贴现率的方法，其实，在计算社会教育收益率和社会教育内部回收贴现率时，方法相类似，也要进行贴现。不过，社会教育总收益净现值，等于社会教育总收益现值减去社会教育总成本现值。其计算公式均同于式（7.3.3）和式（7.3.4），在此不再赘述。