人类的知识：可信度的探讨

第六章　可信度

A.通论

认为全部人类知识在不同程度上都是可以怀疑的看法是从远古就有的；怀疑论者曾经主张过这种看法，在柏拉图学园的怀疑时期这种看法也流行一时。莎士比亚这样揶揄过最可笑的极端的怀疑主义：

不相信星辰是火团，

不相信太阳的运转。

在他写诗的时候，哥白尼早已对后一句话提出了怀疑，不久以后开普勒和伽利略也提出了更为有力的怀疑理由。前一句是荒谬的，如果“火”是按照化学中所讲的那种意思的话。许多看来无可置疑的事物现在已经被人看出很可能是错误的。科学理论本身随着新的证据的积累而不断发生变化；慎重的科学家对于一种新的科学理论不会再抱有中世纪人们对于托勒密学说所抱的那种信心。

但是尽管我们愿意当作“知识”来看的那种东西的每一部分在某种程度上可能都是可以怀疑的，显然某些事物几乎是确定无疑的，而另外一些事物则是毫无把握的揣测。对于一个有理性的人来说，存在着一个表示不同程度的怀疑的尺度，这个尺度的一端是简单的逻辑和算术上的命题以及知觉判断，另一端则是类似麦西尼^[8]人说的是什么语言或者希腊神话中妖女唱的是什么歌那样的问题。我们的最无可置疑的信念是否带有任何程度的可疑性不是我们现在需要研究的问题；我们只需要研究任何一个我们具有合理根据而对之抱有某种程度的相信或不相信的命题在理论上都可以排列在一个以必然的真理和必然的荒谬为两端的尺度之上。这些极端是否可以包括在这个尺度之内，我们可以暂时作为一个悬而未决的问题。

数学上的概率和可信度之间存在着某种关联。这种关联是：如果一个命题对于所有有关证据来说具有某种数学上的概率，那么这就确定了它的可信度的大小。举例来说，如果你正要掷骰子，“掷成双六”这个命题只有“掷不成双六”这个命题所具有的可信度的三十五分之一。所以对于每个命题都给予适当的可信性的有理性的人只要可能就将以数学的概率论作为行为的指导。

可是“可信度”这个概念在应用范围上却比数学上的概率的概念广泛得多；我认为它适用于每个命题，除了那些既不是数据又不是以有利于或不利于承认这些数据而与这些数据相关的命题。我特别认为它适用于那些已经尽可能接近于只表示数据的命题。如果这个看法在逻辑上站得住的话，我们就必须认为一个命题所具有的可信度本身有时就是一种数据。我认为我们应当认为一种数据所具有的可信度有时是一种数据，有时（也许永远）却不具备必然性。在这种情况下，我们可以认为只有一种数据，即一个具有可信度的命题；我们也可以认为这种数据与它的可信度是两种不同的数据。我将不去研究在这两种看法当中我们应该采纳哪一种看法。

一个不是数据的命题可以由许多不同的来源取得可信性；一个想证明自己清白无罪的人可以同时根据本人不在现场和他以前的良好品德来进行辩护。有利于一种科学假说的理由实际上永远是几方面合成的。如果人们承认一种数据可能不具备必然性，那么它的可信度可能由于一种论证而增加，或者与此相反，它的可信度可能由于一种反面论证而变得很小。

一个论证带来的可信度是不能单纯估计出来的。首先让我们看最简单不过的情况，即其中前提具有必然性而论证在正确有效的情况下具有证明性质。在每一步我们必须“看清”这一步的结论得自它的前提。有时候这很容易；比方说，如果论证是巴巴拉式的三段论法。在这种情况下，前提与结论之间的关联所具有可信度几乎就是必然性，结论几乎和前提具有同样的必然性。但是在一个困难的数学论证中，推理上发生谬误的机会就大得多。在一个高明的数学家看来，逻辑关联可能十分清楚，而一个学生却只能偶尔才察觉到这种关联。这个学生相信这一步的正确性的理由并不完全是逻辑上的；这些理由有一部分来自权威方面的论证。这些论证绝不是证明性质的，因为就连最高明的数学家有时也会发生错误。根据这一类的理由，像休谟所指出的那样，一个长的论证的结论比一个短的论证的结论具有较小的必然性，因为在每一步都有某种发生谬误的危险。

通过某些简单化的假说，我们可以把这种不确定性的来源限制在数学的概率论的范围之内。假定人们已经证实在数学的某一分支中，高明的数学家在所有实例中就论证中的一步来说推理正确的比例是x；那么他们在n步的论证中推理一直正确的机会就是xⁿ。由此可以看出，一个不曾通过重演加以证实的长的论证有着相当大的发生推理谬误的危险，即使x接近于1也是这样。但是重演可以把这种危险缩小到很小限度。所有这些都在数学的概率论范围之内。

然而，超出数学的概率论的范围之外的却是个别数学家在推论每一步时所抱的个人的信心。这种信心将随着这一步的困难与复杂而有着程度上的不同；但是尽管存在着这种不同，它却必须与我们对于知觉对象所抱的信心一样直接无间。为了证明某一个前提蕴涵某一个结论，我们必须“看清”每一步；我们只能通过把这一步分解为若干更小的步骤来证明这一步的正确，然后我们又必须把每一更小的步骤“看清”。除非我们承认了这一点，否则一切论证都将消失在无止境的后退中。

到现在为止，我一直在讲证明性质的推理，但是就我们目前的问题而论，非证明性质的推理并没有带来什么新的问题，因为像我们所看到的那样，即使是证明性质的推理在由人来完成时也只能给结论以概然性。人们甚至不能说自命是证明性质的推理总比被认为只具有概然性的推理具有更高程度的概然性；传统的形而上学有不少关于这一方面的例证。

如果——像我所相信并且像我将在适当时候加以论证的那样——数据以及推理结果可以不具备最高的可信度的话，那么数据与推论出来的命题之间的认识论方面的关系就变得比较复杂起来。比方说，我可以认为我回想起了某件事情，但是又找到理由相信那件我似乎回想起来的事情从来也没有发生过；在这种情况下，我可能由于论证而不承认数据。反过来说，当数据本身没有很高程度的可信性时，它却可以由于外界的证据而得到肯定；例如，我可能隐约回忆起和某某先生在去年某时一起吃过饭，并且我可能找出我去年日记上有一个项目证实我的记忆。由此可以看出，我的信念当中每一个信念都可能由于与其他信念联系起来看而得到加强或减弱。

然而数据与推理之间的关系却仍然是重要的，因为相信不管什么事物的理由在经过充分分析之后，都必须在数据上，并且只有在数据上找到。（这里我是把任何可能涉及的推理中所使用的那些原理也包括在数据之内。）由此得出的结果是：有关某种个别信念的数据可能比我们初次看到它们时所显示的要多得多。让我们再举记忆的例子。我想起一件事情这个事实就是这件事情曾经发生的证据，尽管不是决定性的证据。如果我找到这件事情的当时记录，那就成了证实这件事情的证据。如果我找到许多这类记录，那么证实这件事情的证据就得到了加强。如果发生的那件事情是一件像金星横过日面那样由于一种已经巩固地建立起来的科学理论而变得带有必然性的事情，我们就必须把这件事实加到那些记录之上，作为一个附加的相信理由。这样，一方面存在着只是论证的结论的信念，另一方面在知识的合理表述中却不存在只是前提的信念。在我这样讲的时候，我用的不是逻辑上的而是认识论上的说法。

这样我们就可以把一个认识论的前提定义为一个本身就带有某种程度的合理可信性的命题，而不是依靠它与其他命题的关系。每个这样的命题都可以被用来加给那些不是从它推导出来就是与它有着一种概率关系的命题以某种可信度。但是每经过一步，原有的可信性就减少一些；这种情况和财产每经一次继承由于付出死亡税而减少一样。如果把这个类比再往前推进一步，我们可以说本来的可信性类似一个人自己挣得的财产，而作为论证结果的可信性则类似继承的财产。这个类比的成立在于一个已经挣得一份财产的人也可以继承一份财产，尽管每份财产的最初来源一定不是继承。

我打算在本章内讨论可信性，首先把它和数学的概率，再把它和数据，然后再把它和主观必然性，最后把它和合理的行为联系起来加以讨论。

B.可信性与频率

我现在要讨论这个问题：如果已知某个φ x，那么在什么外界条件下从ψ x的频率中得出一个命题a的可信性？换句话说，如果“φ a”是“a是一个α”，那么在什么外界条件下从一个或更多个具有“α的分子中有m/n是β的分子”形式的命题中得出“a是一个β”的可信性？我们将发现，这个问题并不像我们应当问的那个问题那样具有普遍性，但是我们首先讨论它还是可取的。

常识似乎明确地认为：在数学概率的典型例证中，它就等于可信度。如果我从一副纸牌中随便取出一张纸牌，那么“纸牌是红的”的可信度恰好等于“纸牌不是红的”的可信度，因而每一种的可信度都是1/2，如果1代表必然性的话。就一个骰子来说，“最上方是1”的可信度恰好等于“最上方是2或3，4，5，6”的可信度。因此我们可以把数学的概率论中所有推导出来的频率都解释为推导出来的可信度。

在把数学的概率翻译成可信度的这个过程中，我们使用了一个数学的概率论并不需要的原理。数学的概率论只是计算各种情况；但是在这个翻译过程中我们却必须认识到或者假定每一种情况都是同样可信的。这个原理的必要性很久以来就已经披人认识到；人们把它叫作不充足理由原理，或者（按照凯恩斯的说法）无差别原理。我们曾经把这个原理和凯恩斯联系在一起加以研究，但是现在我们却必须单独来研究它。在对它进行讨论之前，我愿意指出这个原理在数学的概率论中并不是必要的。在这种理论中，我们只需要知道各种不同的类的数目。只有在我们把数学的概率当作可信性的尺度时我们才需要这个原理。

我们所需要的原理大致如下：“已知一个客体a，关于它我们想知道‘a是一个β’这个命题具有多大的可信度，并且已知我们仅有的有关知识是‘a是一个α’，那么‘a是一个β’的可信度就是由α和β共有的分子数与α的分子数之比所确定的数学概率。”

让我们再一次举一个说过的实例来说明这一点，那就是美国身材最高的人居住在衣阿华州的机会。这里我们一方面有一个描述d，我们知道它适用于A₁，A₂，……A_n有姓名的人当中的一个并且仅仅一个，其中n是美国的居民数。这就是说，我们知道在“d＝A_r”那些命题中有一个并且仅仅一个（这里r是从1到n的数）为真，但是我们不知道是哪一个。如果这真是我们的全部有关知识，我们就认为“d＝A_r”这些命题中任何一个都和任何另外一个同样可信。在这种情况下，每个命题都具有1/n的可信性。如果衣阿华州有m个居民，“d居住在农阿华州”这个命题的意义就等于“d＝A_r”这些命题中m个命题的一个析取命题，因而为它们当中任何一个命题的可信性的m倍，因为它们是互相排斥的。所以它具有一个由m/n来确定的可信度。

当然在上面的实例中“d＝A_r”这些命题并不都属于同一等级。证据可以使我们把儿童和矮子，多半还把妇女除外。这就表明这个原理可能难以应用，但是并不表明它为伪。

从一副纸牌中抽取一张纸牌的情况更接近于实现这个原理所要求的条件。这里“d”这个描述是“我要抽出的那张纸牌”。52张纸牌都具有可以被我们当作名字的东西：黑桃2等等。这样我们就有52个“d＝A_r”命题，其中有一个并且只有一个为真，但是我们却没有任何使我们选择一个而不选择另一个命题的证据。所以每一个命题的可信性是1/52。如果我们承认这一点，那么它就把可信性和数学的概率联系起来。

因此我们可以提出下面的公理，作为“无差别原理”的一种可能的形式：

“已知一个描述d，关于它我们知道它适用于a₁，a₂，……a_n等客体中的一个并且仅仅一个，并且已知我们不知道任何有关这个描述适用于这些客体中哪一个的问题的知识，那么n个‘d＝a_r’（1≤r≥n）的命题就都是同样可信的，因而每个命题都有1/n大小的可信性。”

这个公理比起一般所说的不充足理由原理来范围要狭小一些。我们必须研究它是否充分，还要研究我们是否有理由来相信它。

让我们首先把上面的公理与上一章所讨论的凯恩斯的无差别原理比较一下。我们记得他的原理是：相对于已知证据来说，p和q的概率是相等的，如果（1）这个证据关于p和q是对称的，（2）p和q是“不可分的”，即p和q都不是具有与它本身形式相同的命题的析取命题。我们认为这种说法可以简化如下：我们说必要的条件是p和q应当是一个命题函项的值，比方说p＝φ（a）和q＝φ（b）；“φ x”不应当包括a或b；并且如果这个证据有一次提到过a，比方说a以ψ（a）的形式出现，它就一定也包括φ（b），并且反过来说也对，这里ψ x一定不再提到a或b。这个原理比起前一节所说的那个原理在某种程度上具有更大的一般性：它蕴涵着后一个原理，但是我却怀疑后一个原理是否蕴涵着它。我们也许可以接受这个更为一般的原理，并把它重述如下：

“已知两个命题函项φ x和ψ x，其中没有一个提到过a或b，或者如果它们提到过a或b，提到的方式是对称的，那么在已知ψ a和ψ b的条件下，φ a和φ b具有相等的可信性。”

如果我们接受这个原理，它将使我们能够从数学的概率推论出可信性，并且使得数学概率论的全部命题可以在能够应用数学的概率论的实例上用来确定可信度。

让我们把上面的原理应用到下面这个实例上来：一个口袋里有n个球，我们知道其中每一个球不是白球便是黑球；问题是：有x个白球的概率是多少？拉普拉斯认为x从0到n的每个值都具有相同的可能性，所以一个已知的x的概率是1/（n＋1）。从纯粹数学的观点看，这是合理的，只要我们从这个命题函项开始：

　　x＝白球数。

但是如果我们从这个命题函项开始：

　　x是一个白球，

我们就得到完全不同的结果。就这个实例来讲，有许多选择x个球的方法。第一个球的选择可以有n个方法；在选择了第一个球之后，下一个球的选择可以有n－1个方法，以此类推。这样选择x个球的方法是

n×（n－1）×（n－2）×……×（n－x＋1）。

这是可以有x个白球的选择方法数。为了得出x个白球的概率，我们必须用选择0，1，2，3或n个白球的方法的和去除这个数。这个和显然是2ⁿ。所以恰好得到x个白球的机会是用2ⁿ去除上面这个数而得到的。让我们把它叫作“p（n，r）”。

当n为偶数，x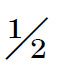＝n时，或者当n为奇数x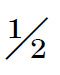＝n±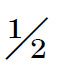时，这种机会最大。在x或n－x小的时候，如果n大，那么它的值就很小。从纯粹数学的观点看，这两个非常不同的结果是同样合理的。但是在我们处理可信度的度量上，它们之间的差别却很大。让我们有某种不靠颜色来分别这些球的方法；例如，把它们从一个口袋中陆续取出来，并且让我们把第一个取出来的球叫作d₁，第二个取出来的球叫作d₂，以此类推。使“a”代表“白”，“b”代表“黑”，并且使“φ a”代表“d₁的颜色是白色”，“φ b”代表“d₁的颜色是黑色”。证据是φ a或φ b为真，但不能两者都真。这是对称的，因而根据证据φ a和φ b具有相等的可信性；换句话说，“d₁是白球”和“d₁是黑球”具有相等的可信性。同样的推理也适用于d₂，d₃，……d_n。这样，就每个球的情况来说，白和黑的可信度是相等的。因此，像一次简单的计算所表明的那样，x个白球的可信度是p（n，x），这里我们假定x位于0和n之间，并包括0和n在内。

我们可以看到在度量可信度上我们假定对于我们的知识来说，数据不仅为真而且还是全部有关的东西；换句话说，我们假定除了数据中所说的东西以外，我们就不知道任何有关的知识。所以就一个在特定时间的特定的人来说，一个特定命题的可信度只有一个正确的值，而在数学的概率论中，对于许多可能是完全假设性的不同数据来说，许多值却是同样合理的。

在把数学的概率计算的结果应用到可信度上的时候，我们必须注意满足两个条件。第一，那些构成数学列举的基础的实例，根据证据来看必须都是同样可信的；第二，这个证据必须包括我们的全部有关知识。关于前一个条件，我们必须讲几句话。

每一个数学的概率计算都从某种基本类开始，例如一块钱币的若干次翻转，一个骰子的若干次投掷，一副纸牌，一个口袋里所有的黑球。我们把这种基本的类的每个分子都作为一来看。由此我们构成其他从逻辑上引导出来的类，例如一块钱币的100次翻转的n个系列所组成的类。从这n个系列中我们可以挑出那些由50个正面和50个背面所组成的次类。或者从一副纸牌开始，我们可以研究由可能分派出的牌组成的类——即13张牌组成的一些选择——并进而探讨这些当中有多少包含同一组牌的11张牌。问题在于计算出来的频率总能适用于具有某种根据这种基本类从逻辑上得以确定的结构的一些类，而为了这个问题的目的，我们把基本类看作由没有逻辑结构的分子组成；换句话说，它们的逻辑结构是无关宏旨的。

只要我们只限于考虑频率的计算——即在数学的概率论的范围内——我们就能以任何一个类作为我们的基本类，并参照它来计算频率。作出一个认为这个类的全部分子都是同样可能的假定是不必要的；我们所需要说的只是：为了当前的目的，我们要把这一个类的每个分子看成一。但是当我们想确定可信度时就需要使我们的基本类由一些相对于证据来说都是同样可信的命题组成。凯恩斯提出“不可分性”的意图就在于保证这一点。我却愿意说基本类的分子必须具有“相对的简单性”，即它们必须不具有可以由数据来下定义的结构。拿一个口袋里的白球和黑球作例。事实上每个球都具有复杂到令人难以置信的结构，因为它由数以万计的分子所构成；但是这与我们的问题并没有什么关系。另一方面，一个从由n个球组成的基本类中选择的m个球的集合却具有一种相对于这个基本类来说的逻辑结构。如果基本类的每个分子有一个名字，那么每个由m项组成的次类就可以得到定义。所有概率计算都必须涉及可以用基本类来下定义的类。但是基本类本身却必须由不能在逻辑上由数据来下定义的分子所组成。我认为当这个条件被满足时，无差别原理总是会被满足的。

可是在这一点上我们却需要慎重。有两种方式可以使“a是一个α”具有概然性，不是（1）因为确知a属于一个大多数是α的类，就是（2）因为a可能属于一个全部由α组成的类。比方说，我们可以说“A先生是有死的”，如果我们确知大多数人是有死的，或者如果我们有理由认为所有的人都是有死的。当我们掷两个骰子的时候，我们可以说：“大概我们不会掷成双六”，因为我们知道大多数掷出的结果不是双六。另一方面，假定我有证据可以认为但并没有证明某种疾病总有某种杆状菌出现；我就可以说，就这种疾病的一个实例来说，大概会有所说的那种杆状菌出现。在每一种情况下都有一种三段论法。在第一种情况下，

　　大多数A是B；

　　这是一个A；(www.xing528.com)

　　所以这大概是一个B。

在第二种情况下，

　　大概凡A都是B；

　　这是一个A；

　　所以这大概是一个B。

可是第二种情况却更难以变为一个频率。让我们探讨一下这是否可能。

在某些情况下，这显然是可能的。例如，大多数的词都不包含Z这个字母。因而如果我们随便选取某个词，那么大概它的所有字母都不是Z。这样，如果A＝所说的那个词的字母组成的类，B＝Z以外的字母组成的类，我们就得到一个属于我们的第二个假三段论法的实例。当然我们必须通过某种方法来给这个词下定义，使得我们暂时对它毫无所知，例如《哈姆雷特》的第8000个词，或者《简明牛津字典》的第248页上第三个词。假定你现在不知道它们是什么词，你打赌说它们不包含Z就不失为聪明。

在我们的第二种假三段论法的所有实例中，显然我一直把它叫作“基本类”的东西是作为由类组成的类来给出的，因而它的逻辑结构是十分重要的。概括一下上面的例子：设х是这样一个由类组成的类，它的大多数分子都包括在某一类β中；那么我们就可以从“x是一个α”和“α是一个x”得出“x大概是一个β”的结论。（就上面的例子来说，x是由词组成的类，α是由某一个词的字母组成的类，β是不包括Z在内的全部字母。）奇怪的现象是用“x的和”来表示由x的分子组成的类，我们的前提不足以证明x的和的一个分子大概是β的一个分子。例如，设x由STRENGTH，QUAIL，MUCK三个词，再加上所有不包括在这三个词里出现的字母的词组成。那么x的和就包括字母表全部的字母，可能不包括Z^[9]。但是“x是一个α并且α是一个x”使得x大概不是在上面这三个词里出现的字母之一，而“x是x的和的一个分子”并不能使这个现象带有概然性。这就具体说明了基本类具有与概率相关的结构时所产生的复杂情况。但是在类似上面的情况中，我们仍然可能用频率来确定可信性，尽管不那样简单。

可是还有另外一类更为重要的情况，我们只有把它们和归纳联系起来看才能对它们进行适当的讨论。这些就是我们具有使得所有的A都是B具有概然性的归纳证据，以及我们推论一个个别的A大概是一个B的情况；例如，大概凡人都有死（不是凡人大概都是有死的），因此苏格拉底大概是有死的。这是属于我们第二种的一个假三段论法。但是如果我们可以把“大概凡人都有死”中的“大概”改变为一个频率，它的改变方法一定不那么简单。因此我将把这一类情况的讨论留给下一阶段。

我们将发现许多不是从频率得出的可信度的例子。对于这些例子我现在就要加以考察。

C.与件的可信性

在这一节里我要提出一个非正统的意见，即与件可能不带确定性。到现在为止存在着两种看法：第一，在知识的明确表达上我们是从本身带有必然性的可以被定义为“与件”的一些前提开始的；第二，既然任何知识都不带确定性，所以并不存在与件，但是我们的合理信念形成了一个关闭的系统。前一种看法是传统的看法，是从希腊人传下来的，在欧几里得几何学和神学中得到了至高无上的地位；后一种看法，如果我没有弄错的话，是黑格尔首先提出的，但在我们这个时代为杜威所拥护而产生了最大的影响。我要提出的是一个折中的看法，但是大体却偏向于传统的看法而不赞成黑格尔和杜威所主张的那种看法。

我把“与件”定义为不依靠从其他命题得出的任何论证，本身就具有某种程度的合理可信性的命题。显然一个论证的结论不能从论证得到比属于前提更高的可信度；因此，如果有合理的信念这类东西的话，那就必然有不完全依靠论证的合理信念。由此并不能得出这个结论：有着完全不是从论证得出其可信性的信念，因为一个命题可能同时本身可信而又是从其他本身可信的命题得出的结论。但是由此却可以得出这个结论：每个不管具有多大程度的合理可信性的命题一定不是（a）只靠它本身，就是（b）只作为本身具有合理可信性的前提的结论，不然就是（c）因为它本身具有某种可信度，并且还是通过证明性的或概然性的推理从本身带有某种可信度的前提得出的结论。如果所有本身多少具有可信性的命题都带有必然性，（c）这种情况就没有什么重要性，因为任何论证也不能使这类命题带有更多的必然性。但是按照我所主张的看法，（c）这种情况却具有最大的重要性。

凯恩斯采用了传统的看法，他在他写的《概率论》第16页上曾经提出这种看法。他说：

“为了使我们对于具有低于必然性的概率的p可以抱有合理的信念，我们就必须知道一组命题h，并且还要知道某个断言p与h之间的概率关系的次要命题q。”

“在上面这个说明中，我们排除了一种可能性。人们假定我们对于p不能抱有程度低于必然性的信念，除非靠知道属于上面所说类型的一个次要命题。换句话说，这类信念只能通过觉察到某种概率关系而产生。……所有通过对于直接认知的客体的观照这种完全直接的方式，而不是掺有任何论证以及通过对于任何其他知识对它的逻辑关系的观照，而得到的知识相当于必然的合理信念而不是只具有概然程度的合理信念。”

我想批驳这种看法。为了这个目的我将考察（1）模糊的知觉，（2）不确实的记忆，（3）对于逻辑关系的模糊不清的认识。

1.模糊的知觉看下面这类常见的经验。（a）你听见一架飞机掠空而过；最初你确信你听见了这种声音，最后你确信你听不见这种声音，但是中间有一段时间你却不能确定你仍然听到还是不再听到这种声音。（b）你在天明时观看金星；最初你看见这颗行星照耀得很明亮，最后你知道日光已经使它看不见了，但是介乎这两个时间之间这一段时间你可能怀疑你是否仍然看得见这颗行星。（c）你在旅途中可能带上许多跳蚤；你开始驱除它们，最后你确信你已经达到目的，但是在中间一段时间你却不时受到可疑的痒的感觉的袭击。（d）你错用了盛醋的壶来煮茶，结果糟不可言。你把壶刷洗一遍再用，但是那种不好的味道无疑仍然存在。经过第二次刷洗，你就怀疑你是否还能尝到醋的味道；经过第三次刷洗，你就确信不再尝到醋的味道了。（e）你的下水道坏了，你请来一位管匠。最初在他修理之后你确信那股难闻的气味已经消失，但是经过不同程度的怀疑阶段，你会逐渐确信又闻到了那股气味。

这类经验是大家都熟悉的，任何关于以感官知觉为基础的知识的理论都必须把它们考虑进去。

2.不确实的记忆在《暴风雨》（第一幕，第二场）中，普罗斯波罗让米兰达探索一下“过去时光的黑暗深渊”；她说：“我不是有四五个侍女照管过我吗？”接着普罗斯波罗证实了她的带有怀疑的回忆。我们大家都有过这类感到不十分确实的记忆。一般来说，如果值得做的话，我们能够从其他证据来判断记忆是否确实，但是这对于我们当前的题目却没有关系，我们当前的题目是记忆本身具有某种程度的可信性，尽管这种程度远远够不上完全的必然性。一个具有相当大的可信度的记忆对于使我们相信某件我们对之具有其他证据的过去发生的事件的理由来说也构成一个增添的因素。但是这里必须明确一点。记得不确实的过去事件本身就有部分的可信性；但当我把回忆当作相信的一个理由时，我就不再把过去发生的事件当作与件，因为作为与件的并不是过去发生的事件而是现在的回忆。我的回忆给予被忆起的事件以某种可信性；至于可信性有多少，这一点我们可以根据关于记忆错差的频率统计研究以归纳方法大体断言出来。但是这与作为与件来看的过去发生的事件却是两回事。这类与件必须由记忆补充是一个我已经在别的地方讨论过的题目。

3.对于逻辑关系的模糊认识任何一个不具超人数学能力的人，如果他研究过数学的话，一定经常遇到几乎不能“看出”一个证明中某一步的经验。理解一个证明的过程由于把步骤划得很小而变得比较容易，但是不管我们把步骤划得多么小，在问题非常复杂的情况下总有一些步骤是困难的。显然如果我们已经尽可能地把步骤划得很小，每个步骤就必然是一个与件，因为不然的话，每一个企图证明的努力都会陷入没有止境的后退。比方说让我们看一个巴巴拉式的三段论法。我说：“凡人皆有死”，而你的意见也和我一致。然后我说：“所以苏格拉底有死”，而你却说：“我看不出这个结论是怎样得出来的。”在这种情况下我怎么办呢？我可以说：“你看不出如果f（x）永远为真，那么f（a）为真吗？你看不出因此如果φ（x）永远蕴涵着ψ（x），那么φ（苏格拉底）就蕴涵着ψ（苏格拉底）吗？你看不出我能让‘x是一个人’代替‘φ x’，并且让‘x是有死的’代替‘ψ x’吗？你看不出这就证明我的论点了吗？”一个学生能够理解这套说法而不能理解原来的三段论法肯定是个心理学上的怪物。而且即使有这样一个学生，他还是必须“看出”我的论证中的步骤。

由此可以看出，当我们把一个论证讲得尽可能简单的时候，每一步中所断言的关联就必须是一个与件。但是每一步中的关联都具有最高度的可信性却是不可能的，因为即使是最好的数学家有时也会出错。事实上，我们对于命题之间的逻辑关联的认识就像我们的感官知觉和记忆一样，是可以按照它们的可信度来排列的。在有些认识中，我们对于逻辑关联看得清楚到无可怀疑的地步，而在另外一些认识中，我们对于逻辑关联的认识却模糊到没有把握说出我们是否看到这种关联。

以后我将假定一个与件，按照在本节开始所规定的意思来讲，在或多或少程度上可能是不确定的。我们在理论上可以把这种不确定性和那种从数学的概率得到的不确定性联系起来，如果我们认为一种不确定性可能大于、等于或小于另一种不确定性的话。举例来说，当我认为我听见一种很轻的声音而不能确定有无声音的时候，在理论上我就可以说：这种声音的发生与掷骰子出双六具有同样程度的合理可信性。在某种程度上，这类比较可以通过收集关于模糊感觉的错误证据并找出它们的频率来加以检验。所有这些话都是含糊不清的，我看不出怎样才能把它讲清楚。但是无论如何它让我们想到与件的不确定性具有数量的性质，可以等于或不等于从一个概率推论得到的不确定性。我将假定这是事实，同时也承认在实际应用上难以对与件的不确定性进行数值测定。我们可以说在怀疑使得相信与不相信处于平衡状态时，不确定性就是一半。但是这种平衡只有通过内省才能得到，是不能用任何检验来证实的。

承认与件的不确定性使得计算一个命题的合理可信性的方法变得复杂起来。让我们假定某一个命题p本身具有可信度x，这就作为一个与件；并且让我们假定还有若干命题的一个合取命题h，它本身具有可信性y，根据这个合取命题我们可以通过一个具有可信性z的论证而使p具有可信度w。在这种情况下p的全部可信性是多少？也许我们想说它是x＋yzw。但是h显然除了本身的可信性以外还有推导出来的可信性，这一点也会增加x的可信性。事实上，这些复杂情况很快就变得难于驾驭。这就产生了某种接近黑格尔和杜威的理论的东西。

如果已知许多命题，其中每个命题本身都具有相当高的可信度，并且已知一个推理系统，通过这个系统这些不同的命题可以增加彼此的可信性，那么最后就可能得出一组从整体来看具有很高的可信度的互相关联的命题。在这一组命题之内，一些命题只是通过推理才得出来的，但是没有任何命题仅仅是前提，因为那些是前提的命题同时也是结论。我们可以把知识的大厦比作由许多桥墩支持的一座桥梁，每个桥墩不仅支持着车行道而且通过互相联结的铁梁还能帮助其他桥墩的稳定。这些桥墩相当于本身具有某种可信性的命题，而桥的上部则相当于只是通过推理才得出的命题。但是尽管每个桥墩可以从其他桥墩得到力量，支持全部重量的还是坚实的地面；同样，支持整座知识大厦的还是本身的可信性。

D.主观必然性的程度

主观必然性是一个心理学的概念，而可信性则是一个至少有一部分是属于逻辑的概念。它们之间是否具有任何关联的问题是我们是否具有任何知识的问题的一种形式。这样一个问题在绝对怀疑论的基础上是无法讨论的；除非我们愿意断言某种东西，否则任何论证都是不可能的。

让我们首先区分三种必然性。

1.一个命题函项对于另一个命题函项来说具有必然性，如果满足第二个命题函项的项目组成的类是满足第一个命题函数的项目组成的类的一部分。例如，“x是一个动物”对于“x是一个有理性的动物”来说就具有必然性。这种意义的必然性属于数学的概率。我们将把这种必然性叫作“逻辑上的”必然性。

2.一个命题具有必然性，如果它有着最高度的可信性，不管可信性来自本身还是来自论证。就这种意义来讲，也许任何命题都不具有必然性；换句话说，不管这个命题对于一个特定的人来说带有多么大的必然性，更多的知识还是可能增加它的可信度。我们将把这种必然性叫作“认识论上的”必然性。

3.一个人在他对于一个命题的真理不抱任何怀疑时就认为这个命题具有必然性。这是一个完全属于心理学的概念，我们将把它叫作“心理学上的必然性”。

由于确信的程度达不到主观的必然性，一个人可能或多或少确信某种事物。我们感到确信明天会出太阳，拿破仑也确有其人；我们相信量子论和有过佐罗亚斯德这个人的程度就差一些；对于爱丁敦得出的电子数完全正确，或者在特洛伊城被围时有个名叫亚加梅农的国王，我们相信的程度就更差了。这是一些已经取得一致意见的问题，但是另外还有一些意见分歧的问题。有些人确信丘吉尔是个好人而斯大林是个坏人，其他一些人的意见却正好相反；有些人完全确信上帝站在协约国一边，其他一些人则认为上帝站在德国一边。因此主观的必然性不是真理的保证，甚至也说不上是高度的可信性的保证。

谬误不仅包括那种相信虚伪事物的绝对谬误，还包括那种相对于相信者的知识来说，相信的程度超过或不及被相信的命题应有的可信度所保证的程度而产生的数量性质的谬误。一个完全相信某一匹马在德贝赛马中定能获胜的人即使这匹马真的获胜也算是犯了错误。

从广义上说，科学方法是由目的在于使相信程度和可信度尽可能完全符合的技术与规则组成的。可是除非我们从一些在认识论上看来可信在主观上也接近必然的命题出发，我们是不能着手寻求这种和谐的。这就让我们想到一种笛卡尔式的探讨，但是这种探讨必须具有某种非怀疑论的主导原理才可能获得结果。如果在可信性与主观必然性之问没有任何关系，那就不可能有知识这种东西。在实际应用上我们假定一类信念可以被认为是真的，如果（a）所有仔细研究过它们的人都完全相信它们，（b）没有反对它们的正面论证，（c）没有任何已知理由可以认为如果它们不真人类还要相信它们。在这个基础上，人们一般认为一方面是知觉判断，另一方面则是逻辑与数学，囊括了我们知识中最带必然性的东西。我们将看到如果我们要得到科学的知识，除了逻辑与数学之外，还需要补充某些超出逻辑范围以外的原理，其中归纳是迄今为止（我认为这是错误的）获得最普遍承认的一个原理。这些超出逻辑范围以外的原理提出了一些我们要去研究的问题。

完全的合理性不在于相信真理而在于给予每一个命题以相当于它的可信度的相信程度。就经验命题来讲，可信度是随着新的证据的发现而改变的。在数学中，一个不是数学家的有理性的人会相信别人告诉他的知识；所以在数学家发现他们的前辈著作中的错误的时候，他就会改变他的信念。数学家尽管可能发生错误，他本人还不失为一个完全有理性的人，如果这个错误在当时很难被人发现的话。

我们是否应当把合理性作为目的是一个伦理上的问题。我将在下一节里考察这个问题的某些方面。

E.概率和行为

巴特勒主教所说的“概然性是人生的指南”这句话是大家都熟悉的。让我们简单看一下它可能表示的意思是什么，它在什么范围内是真的，以及相信它具有它似乎具有的真理程度这件事包含着什么内容。

大多数伦理学说都属于两种类型之一。按照第一种类型的说法，好的行为就是遵守某些规则的行为；按照第二种类型的说法，好的行为是为了实现某些目的。还有一些不属于这两种类型的学说，但是就我们的目的来讲，我们可以不必去管它们。

康德和十诫是属于第一种类型的学说的例证。诚然十诫不是这类学说中的完全例证，因为十诫中有些条是有理由根据的。你一定不要崇拜偶像，因为这样上帝会感到妒忌；你应当尊敬父母，因为这样可以减少你的死亡机会。当然，人们可以很容易找到不去杀人和偷窃的理由，但是十诫中却没有讲到这些。如果讲出理由，那就会有例外，一般来说常识已经承认这些例外，但是《圣经》原文中却没有提到它们。

当我们把伦理学当作一些指导行为的规则的时候，概率在这里就不起什么作用。只有在第二种类型的伦理学说，即那类认为善就在于完成某些目的的伦理学说中，概率才是有关宏旨的东西。只就对于概率的关系而论，选择什么样的目的所产生的差别是很小的。为了明确起见，让我们假定选择的目的是使快乐最大限度地超过痛苦，而一次快乐和一次痛苦被认为相等，如果一个具有机会的人对于他是否具有两者或者两者都不具有感到无动于衷。我们可以把这个目的简单叫作得到最大限度快乐的目的。

我们不能说善良的人将按照事实上会得到最大限度快乐的方式行事，因为他可能没有理由期待这种结果。如果希特勒的母亲在他婴儿时期就把他杀死，这会是一件好事，但是她却不可能知道这一点。因而我们必须说善良的人将在他的知识限度之内按照大概会得到最大限度快乐的方式行事。这里所涉及的那种概率显然就是可信度。

我们所谈的这些概率可以用计算“预料”的规则来确定大小。这就是说，如果有一个概率p，它表示某一件行为的结果当中可能有x那样大的快乐，那么这对于预料就提供了px的分量。因为遥远的结果很少有可以看出的概率，这就使得讲求实际的人有理由把目光通常只注意到他的行为的不太遥远的结果上去。

另外还有一种要考虑到的情况：这里涉及的计算常常是很困难的，并且在两种可能行为产生快乐的性质几乎相等时最为困难，在这种情况下选择就变得不重要了。所以一般来讲不值得小心地去确定哪种行为产生最大的快乐。这是使人们赞成行为规则的理由，即使我们的最基本的伦理观并不承认这些行为规则：这些行为规则在最大多数的情况下可能是对的，使我们免于在估计概然性的结果上耗费精力和时间。但是对于行为规则本身人们却应该看其产生快乐的性质而小心地给以肯定，人们在作出真正重大的决定时有必要想到这些规则并不是绝对的东西。币制改革通常就包含着某种类似盗窃的行为，而战争就要杀人。决定是否改革币制或宣布战争的政治家必须深入考察这些行为规则，尽全力估计到可能的后果。只有在这种意义下，概然性才能作为人生的指南，并且只有在某些外界条件下才是这样。

可是这句格言还有另外一种比较平易近人的意思，也许这是巴特勒主教所要说的意思。这就是我们在实际生活中把具有很高程度概率的事物看成带有必然性的东西。这仅是一个常识问题，不会引起有关概率论的任何争论。