拉格朗日等边三角形解与小行星群

拉格朗日等边三角形解与小行星群

大约300年前，牛顿在开普勒、伽利略等人工作的基础上总结出力学三大定律，并提出了万有引力定律。之后，力学就获得了大踏步酌进展。

和一切科学一样，天体力学至今远未达到尽善尽美的程度。300年前，牛顿的理论一提出，“二体问题”——两。个均匀的球形天体，在相互引力作用下的运动——就得到了彻底的解决。人们辛辛苦苦研究了300年，天体力学能彻底解决的基本问题仍然只是这一个!哪怕再加上一个天体(“三体问题”)都不行。甚至，连这个“三体问题”能不能彻底解决，也还没有人能说清楚呢!

3个世纪以来，著名的三体问题还只得到了有限的进展。在这些进展中最著名的大概要算拉格朗日的解了。

拉格朗日是法国数学家。他在数学和力学中都作出了杰出的贡献。1006号小行星便以他的名字为名。

1772年，也就是在提丢斯再次提出他的行星距离定律的时候，拉格朗日发表了他的论文《三体问题论》，在费了不少心血之后，他仍无法得到三体问题的一般解，只好用一个非常特殊的例子作为一个结果。当时看来，这个例子简直是纸上谈兵，纯粹只是一个有趣的数学游戏而已。

拉格朗日指出，如果某一时刻三个天体恰好处在一个等边三角形的三个顶点上，那么在某种特定的初始相对速度下，它们就会始终保持着等边三角形的队形如下图，这时，三个天体都以同一个周期，绕它们的公共质心作椭圆(三个椭圆的划、不一定相等，但形状相似)运动，而这个三角形则以同样的周期作膨胀和收缩。如果三体的初始相对速度为0，那么它们就以圆形轨道运行。这时三角形的大小始终不变。

拉格朗日的等边三角形解

拉格朗日这篇出色的论文获得了巴黎科学院的奖金。不过(包括拉格朗日在内)谁也没有认真看待这个特解，觉得它有什么实际意义。

平运动近于300″(略等于木星的平运动)的小行星在天体力当中很有理论的意义。若空间仅有两个星体互相吸引绕转，这就是所谓的二体问题，它们在各时刻到达的位置可以从轨道要求作出预报来。只要再多一个星体就是三体问题，对于这样的问题，一般的数学问题都不能彻底加以解决。只有当其中二星体的质量远小于第二星体时，才可以借助所谓摄动理论求得逐步接近的近似值。在18世纪末期，数学家拉格朗日证明，三体问题在一个特殊情况下，即其中一星体质量微小，而三体在运动中恰好位于等于三角形的3个顶点时，是可以得到精确解答的。一颗小行星在太阳和木星作用下的运动，由于行星质量微小，就形成这样的特殊情况。这时小行星有5处称为平动点的位置。所谓平动点，就是小行星在太阳和木星的引力场中能达到稳定平衡的位置。如果位于平动点的小行星受到其他外力作用而偏离平动点，它也会立即回到平动点，而不会飞离。这就好像位于碗底;的一个小球，它的平衡是稳定的，即把它向旁边拨一下，仍会滚回原处。这一根据天体力推出的理论，由于1906年发现588号小行星而得到证实。这颗小行星果然是守在平动点L₄附近活动，而且由于木星绕日运动，小行星也随着平动点以同木星运动相同的角速度每日300″绕日运动。以后在平动点上L₄和L₅，处又陆续发现了一些小行星，它们的平运动都在300″左右，这一类小行星统称为脱罗央群，已发现了20颗左右。半夜里，在天空正背向太阳的方向上，我们有时可以看到一团比银河还要稍微暗淡的白光，天文学上叫作对日照。这光团就是逗留在图7平动点L₂(图中木星要换成地球)处的一团反射着阳光的宇宙尘埃。这也是平动点理论的一个证据。

1906年2月22日，发明照相法寻找小行星的沃尔夫，又发现宁1颗小行星。这颗小行星异常缓慢的运动(只及一般小行星的1/3)，引起了天文学家的特别注意。经计算，它与太阳的距离是5.2天文单位，与木星相同。即差不多与木星处在同一条轨道上，但位置在木星前约60°的地方，俨然像“木大人”的一位开路先锋。因此，这颗小行星与木星、太阳三者正好构成了拉格朗日特解的情况，成为天空中一个奇妙的正三角形。后来，它被编为588号，并命名为阿基琉斯(Achilles)。阿基琉斯是荷马史诗《伊利亚特》中最伟大的希腊英雄。同一年，又有人发现了跟在木星之后的“随从”，它与木星相差也正好是60°左右，也就是在第二个拉格朗日三角形点上。它被编为617号小行星，并取了阿基琉斯的亲密战友帕特罗克勒斯(Patroclus)的名字。

(www.xing528.com)

拉格朗日点与脱罗央群小行星

以后，在这两个点(也称拉格朗日平均点)附近又陆续发现了许多小行星。它们都用《伊利亚特》所描述的特洛亚战争中英雄的名字命名。所有这些小行星统称为脱罗央(即特洛亚)群小行星。还作了规定:第一平动点(L₁，见下图，附近的叫希腊群，以攻打特洛亚城的希腊英雄命名。第二个点L₂的周围的叫纯脱罗央(Pure Trojan)群，以特洛亚城的保卫者命名。不过每一群都有一个例外，因为在作这个规定之前，帕特洛克罗斯和赫克托尔都已陷入敌阵了。

希腊群小行星

(2260)为我国紫金山天文台发现，又名“昆仑”。

纯脱罗央群小行星

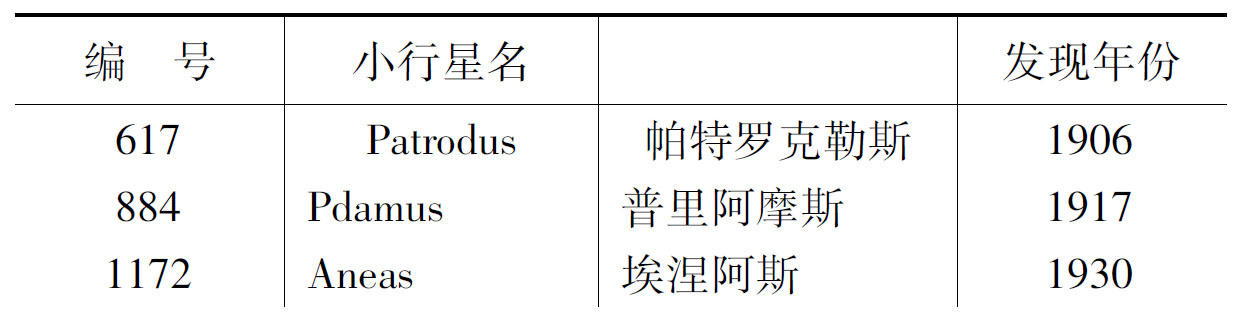
*2223为我国紫金山天文台发现，又名，“喜玛拉雅”。

到目前为止，这类小行星具备命名条件的已有31颗。其中17颗属希腊群，14颗属纯脱罗央群。

分别属于纯脱罗央群和希腊群。按国际习惯，前者命名为萨耳珀冬(特洛业人的盟友，吕喀亚国王，在战争中为帕特洛克罗斯所杀)。后者命名为涅俄普托拉摩斯(阿基琉斯的儿子)。

通常情况下，纯脱罗央媲美小行星都在平动点附近作周期性的摆动。但是如果我们认为它们的队列操练真如仪伏队那样齐整，那就错了，这些小家伙才不那么规矩呢:它们的轨道倾斜有时可以超过20°，它们的平均经度有时也会偏差到10°～20°，这使它们的实际位置与理论位置的差别最大可达1.6亿千米，比地球到太阳的距离还要远呢!结果它们的实际运动非常复杂。而且，土星引起的摄动，不但会改变它们的位置，还会将它们中的个别成员逐出这两个小集团，或为它们吸收进新伙伴。