嵌入式实时数据库系统的数据组织及处理技术

8　数据组织

嵌入式数据库系统通常应用于具备自主控制能力的设备中，进行无人干预地运行，比如，无人驾驶汽车（及各种飞行器）的导航系统、机器人的控制系统、各种航天器的数据处理系统等。嵌入式数据库系统所处理的事务常常是实时事务，事务调度的正确性依赖于高效的处理和预测能力。嵌入式数据库系统中常常采用主存数据库技术，存取机制的主要目标是综合提高CPU的利用率和节约主存空间。经典的存取机制主要分三大类：一类是基于HASH函数的存取机制，比如，可扩展HASH（EH）［3］、线性HASH［4］、受控查询多方向HASH（CSMH）［5］等；另一类是基于查询树的存取机制，比如，B树、B＊树、AVL树、T树、T＊树［2］等。除此之外，Chanho Ryu等提出了一种综合了HASH表和查询树特点的存取机制Hybrid－TH［1］，已经证明它显著提高了查询效率。本书提出的H－T树是对Hybrid－TH的改进，它能适应嵌入式数据库的要求。

8.1　传统的内存索引结构

8.1.1　AVL树

AVL树也叫二叉平衡树，由AT—T BELL实验室提出，它要么是一颗空树，要么其左右子树的深度之差不超过1，并且，其左右子树也是二叉平衡树。定义二叉平衡树上某结点的平衡因子为该结点左子树的深度减右子树的深度，因此，所有结点的平衡因子只能是－1、0或1（见图8．1）。

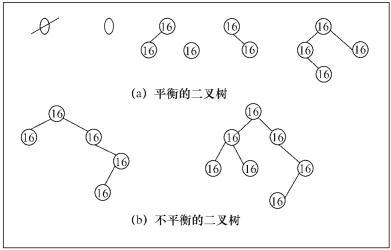
图8.1　平衡的二叉树和不平衡的二叉树

对AVL的插入操作在叶子结点上进行，一旦AVL的平衡性被破坏，则必须通过旋转进行调整，恢复其平衡性。假设AVL树中有n个结点，则该AVL树的深度为O（），平均查找长度为O（），但是，AVL的最大缺点是空间利用率不高。

8.1.2　B-树

B－树是一种平衡的多路查找树，与AVL树相比，B－树的每个结点中有多个数据成员。一个m阶的B－树要么为空树，要么满足下面的条件：

①树中每个结点至多有m棵子树。

②除非根结点为叶子结点，否则至少有两棵子树。

③除根之外的所有非终端结点至少有棵子树。

④所有非中断结点中包含下列信息数据：

（n，A0，K1，A1，K2，…，Kn，An）

其中，Ki（1≤i≤n）为关键字，且Ki（1≤i≤n）

Ai（0≤i≤n）为指向子树根结点的指针，且Ai（0≤i≤n）所指子树中所有结点的关键字都小于Ki＋1，An，所指子树中所有结点的关键字都大于n （n为关键字的个数，或n＋1为子树个数）

⑤所有的叶子结点都出现在同一层次上，并且不带信息（可以看做是外部结点或查找失败的结点，实际上这些结点不存在）。

图8.2　B-树　结点示例

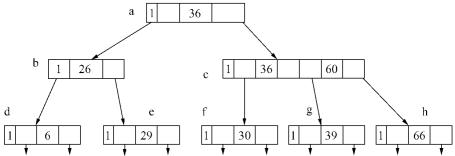
图8.3　B-树　示例

对于深度为L＋1的M阶B－树而言，计算其最少结点数的方法如下：

根据B－树的定义，第一层至少有1个结点，第二层至少有2个结点，由于除根之外的每个非终端结点至少有［m/1］棵子树，则第三层至少有2［m/2］个结点……依次类推，第L＋1层至少有2（［m/2］）l－1个结点，而L ＋1层的结点为叶子结点。若m阶B－树中具有N个关键字，则叶子结点即查找不成功的结点为N＋1，由此：

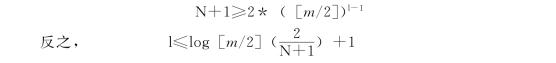
在含有N个关键字的B－树上进行查找时，从根结点到关键字所在结点的路径上涉及的结点不超过

8.1.3　线索二叉树

二叉树中存在大量的空指针，为了减少这种浪费，A．J．Perlis和 C．Thornton用线索代替空指针，线索指向树中的其他结点，左边的空指针处放置的线索指针指向该结点的前序结点，右边的空指针处放置的线索指针指向该结点的后续结点，这样的树叫线索二叉树。根据周游树的顺序，线索二叉树分为前序周游线索二叉树、中序周游线索二叉树和后续周游线索二叉树。如图8．4所示，图中的虚线表示线索，二叉线索树中每个指针只需要1bit的位置标识该指针是该子指针还是线索指针，只有叶子结点才会有线索指针，具有两个该子的结点没有指向后续结点的指针。

图8.4　TB-树及其结点H

8.1.4　T-树

T－树是Lehman提出的适用于主存数据库系统的索引结构。它是在一个结点中有多个数据对象的二叉树，遵循AVL的特性，在每个结点中，数据对象按升序排序，指针parent pominter、left child pointer和right child poninter分别指向该结点的父结点、左子树和右子树。

如图8．5所示，在每个结点上，小值在左边，大值在右边。对于每个内部结点A，有一个叶子或半叶子结点，它上面的数据值是A结点最小值的前序，同样，存在一个叶子结点或半叶子结点，它上面的值是A结点最大值的后续，前序值叫A的最大下限GLB（greatest lower bound），后续值叫A的最大上限。

为了区别普通指针和线索指针（见图8．6），在每个结点上设置两个逻辑位：LBIT和RBIT，如果LBIT为真，表示左指针是指向左的指针，否则，左指针指向前序结点，RBIT的作用与此相似，它标明右指针的含义。

实验表明：对于主存数据库系统，在数据对象有序时，T－树的性能好于AVL－树、简单的数组和B－树。

图8.5　T-树的结点

图8.6　T-树的结构

8.1.5　T＊-树

T＊－树的结构与T－树非常相似，不同的只是在每个结点上有一个指针指向该结点的后续结点，通过该指针，大大提高了查询效率，如图8．7所示。

8.1.6　Hybrid-TH

①Hybrid－TH将树索引和HASH索引有机地结合起来，大大降低了查询的时间复杂度，Hybrid－TH由一个树和Hash表组成，Hybrid－TH的结点与T－树结点相同，Hash表就是普通的Hash表，只是其冲突处理结构（溢出链）中包含了一个指针，该指针指向Hybrid－TH中的结点，当Hybrid －TH中某结点上的值被移动到新的结点时该指针必须被修改。

如图8．8所示，Hybrid－TH中Hash表的每个元素有三个域：

图8.7　T＊-树

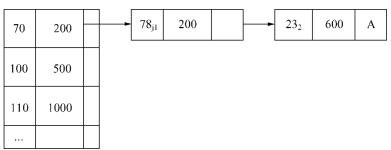
图8.8　Hybrid-TH中HASH表结构

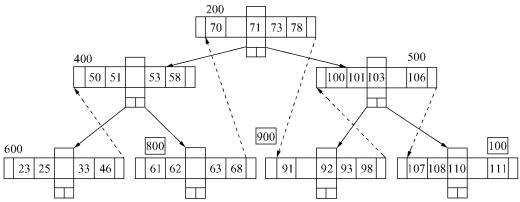
图8.9　Hybrid-TH＊-树的结构

②数据对象的关键字。

③结点指针，该指针指向该数据对象所在的树结点。

④溢出指针，该指针指向溢出链。

在图8．8中，关键字为70的元素在地址为200的结点上，关键字为78和23的元素在Hash表中与关键字为70的元素发生冲突，在Hash表中，它们被放置在相应的溢出链上，而溢出链中表明了这两个元素的值分别在地址为200和600的树结点中。

8.2　H-T及其存取方法

8.2.1　H-T的结构

H－T（Hash－Tree）是对Hybrid－TH的改进，由两部分组成：一个Hash表和N个树。

定义8．1：H－T由一个HASH表和一组T＊树组成，H－T：：＝（HASH，T），

其中：HASH：：＝｛＜valuei，linki＞｜1≤i≤b，linki指向一个树Ti｝

T：：＝｛Ti｜1≤i≤b｝

Ti 满足以下条件：

①Ti是一个AVL树。

②每个结点上最多k个数据元素，有指针分别指向其父结点、左子树、右子树和后续结点。

③结点上的数据对象按关键字进行升序排序。

Hybrid－TH和H－T的区别如下：

①Hybrid－TH中有一个T树，H－T中有多个T＊树。

②一个数据元素在Hybrid－TH的HASH表中占用一个（data，link）位置，在树中又占用一个（data，link）位置，而它在H－T的HASH表中最多占用一个（data，link）位置。

③Hybrid－TH的查询负担主要集中在HASH表中，而H－T的查询负担主要集中在T＊树中。

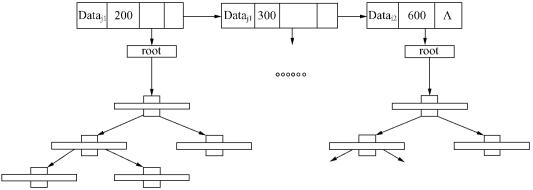
图8.10　H-T的结构

定义8．2：H－T中的一个树称为H－T的原子树，H－T中表的长度称为H－T的离散度，记做δ（H－T），H－T的树结点所能容纳的数据数称为H－T的聚合度，记做ξ（H－T）。对于一个H－T的树结点，当其容纳的数据数等于聚合度时，该结点称做满结点。

离散度表示HASH分散数据的能力，聚合度反映连续空间的大小。

8.2.2　H-T的有关操作

（1）简单查询算法和范围查询算法

H－T中的简单查询从计算相应的HASH函数值开始，查询HASH表，然后查询T＊树，查询关键字为key的数据的具体算法如下：

输入：数据ob，H－T的头指针hh

输出：指向ob的指针q(www.xing528.com)

算法：

第一步：if（j valuej（｛＜valuei，linki＞｜1≤i≤b｝（valuej＝f（ob．key）then go to step 2else｛q：＝null；go to step 3｝

第二步：if（（nodek（Tjnodek．max≥ob．key≥nodek．min）（（（nodek．keyqq＝＝ob．key）

then q：＝nodek．linkqq else q：＝null；

第三步：return（q）

查询数据集D＝｛di｜di（［datal，datau］｝称为范围查询，它是在简单查询的基础上进行的，在查询到下限数据p＾data［i］（［datal，datau］后，取该数据并继续比较后续数据直到p＾data［j］≥datau，如果在此之前，已比较完该结点的所有数据则沿succ找到。

（2）插入算法

H－T插入运算根据HASH表找到对应的原子树，新值将插入到该树中，如果插入引起树的不平衡，则需调用平衡算法，使树保持平衡。具体算法如下：

输入：数据ob，H－T的头指针hh

输出：成功则返回T，否则返回F。

算法：｛insert（p，a）在结点p中插入元素a，balance（t）检查树t，如果不平衡，则调用平衡算法使之恢复平衡。Divide（p，a）以a为界分裂结点p．insert（a，p，h）将（hash（a），p）插入HASH表。｝

第一步：if（j valuej（｛＜valuei，linki＞｜1≤i≤b｝（valuej＝f（ob．key）then

｛p：＝new（node）；insert（p，ob）；insert（ob，p，hh）；return（1）｝

第二步：if（（nodek（Tj nodek．max≥ob．key≥nodek．min）then

if（（mm（nodek．linkmm＝null）Then｛insert（nodek，ob），return（．T．）；｝

else｛b：＝nodek．max；remove（b）；insert（nodek，ob）；ob：＝b；go to step 2｝

else｛nodew：＝lastnode（hh）；

if（（mm（nodew．linkmm＝null）then｛insert（a）｝else p：＝new （node）；insert（p，ob）

第三步：if p＜＞null balance（hh）；

（3）删除算法

删除算法通过HASH表找到要删除的数据所在的结点，删除该结点后有可能改变结点的succ，如果该树为空还需将HASH表的相应link置为空。

输入：数据ob，H－T的头指针hh

输出：成功则返回T，否则返回F。

算法：｛delete（p，a）删除结点p中的元素a，join（p1，p2）将两个结点p1，p2合并为一个结点p1，放弃p2．underflow（）下溢处理｝

第一步：if（j valuej（｛＜valuei，linki＞｜1≤i≤b｝（valuej＝f（ob．key）then go to step 2else return（0）；

第二步：if（（nodek（Tjnodek．max≥ob．key≥nodek．min）（（（nodek．keyqq＝＝ob．key）

then delete（nodek．linkqq）else return（0）；

第三步：if underflow then｛underflow（）；balance（hh）；｝

第四步：return（1）．

8.2.3　H-T的性质

性质1：最坏情况下，原子树的结点数为，其中，。

证明：在最坏情况下，原子树的叶子中只有一个数据元素，设树的总结点数为ma，存在关系：

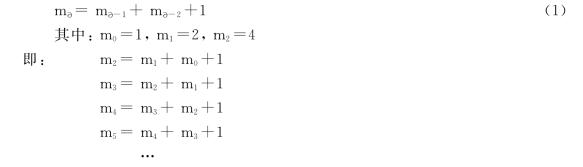
（1）的两边分别同乘xi，i＝2，3，4，…，｜x｜＜1，得：

m2x2＝m1 x2＋m0x2＋x2

m3x3＝m2x3＋m1x3＋x3

m4x4＝m3x4＋m2x4＋x4

m5x5＝m4x5＋m3x5＋x5

…

将它们相加得：

（m2x2＋m3x3＋m4x4＋m5x5＋…）

＝（m1x2＋m2x3＋m3x4＋m4x5＋…）＋（m0x2＋m1x3＋m2x4＋m3x5）＋（x2＋x3＋x4＋x5＋…）

命：G（X）＝m0＋m1x＋m2x2＋m3x3＋…（2）

（G（x）-m0-m1x）＝x2　G（x）＋x（G（x）-m0）＋x2/（1-x）

有：

性质2：最坏情况下，原子树有个叶子结点。

假设原子树中的叶子结点数为yδ，存在关系：ye＝ye－1＋ye－2，

命：F（x）＝y0＋y1x＋y2x2＋y3x3＋…

与上同理可证得：

性质3：若H－T中有n个对象，最坏情况下，H－T的深度为：a＝log2

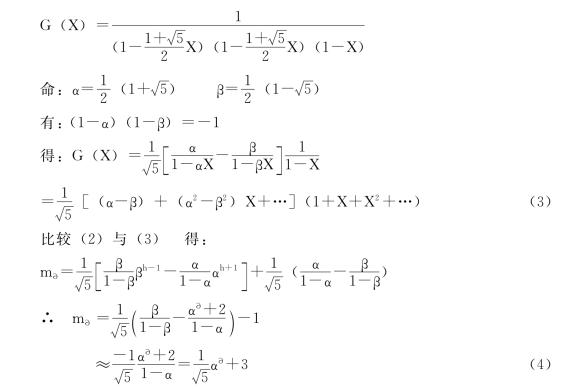
证明：在最坏情况下，所有的数据元素集中在一个原子树中，并且原子树中的深度最长。设原子树中有结点mδ个，其中叶子结点yδ个，则存在以下关系：

ζ（m0－y0）＋ye＝n

由性质1和性质2得：

将上式代入（1），得

8.2.4　性能分析

用μ表示一个链指针所占的空间，ε表示一个数据所占的位置，下面比较容纳n个不同关键字的数据元素时Hbrid－TH和H－T的性能。

①当数据被HASH表和树均匀分布时，Hbrid－TH的空间复杂度为：

Space11＝HASH表占用的空间＋T树占用的空间＜n＊（μ＋2ε）＋（n＊（μ＋ε）＋3nε/ζ）

H－T的空间复杂度是：Space21＜δ＊（μ＋ε）＋（n＊（μ＋ε）＋3nε/ζ）

Hbrid－TH的平均时间复杂度为：Time11＝log2（δ＋n/δ＋ξ），

其中，查询HASH表的最大时间复杂度是：log2（δ＋n/δ）；

H－T的最大时间复杂度为：Time21＝log2（δ＋n/（ξδ）），

其中，查询HASH表的时间复杂度是：log2（δ）。

②在最坏情况下，Hbrid－TH的空间复杂度为：

Space12＝w＊（μ＋2ε）＋St，（if n＞δ then w＝n else w＝δ），

其中，St为树所占用的空间，由于H－T的这部分与此相同，不详细计算；

Hbrid－TH的最大时间复杂度为：Time12＝log2δ＋n＋log2ξ，

其中，查询HASH表的时间复杂度是：log2n；

H－T的空间复杂度是：Space22＝δ＊（μ＋ε）＋St；

最大时间复杂度为：Time22＝log2δ＋log2（4．41n/（5．21＋9．63ξ）/log2α ＋log2ξ，

其中，查询HASH表的时间复杂度是：log2δ。

由于Space11＞Space21，Space12＞Space22，Time11＞Time21，Time12＞time22，可见H－T的性能优于Hybrid－HT。特别指出的是：H－T的插入操作不需修改已有数据元素在HASH表中的指针，而Hbrid－TH却相反。

数据的存取机制关系到系统的效率，在嵌入式数据库系统中，由于内存非常宝贵同时没有费时的I/O操作，存取机制的设计目标是节约存储空间同时尽可能地提高处理速度。H－T与Hybrid－TH相比较，H－T的空间复杂度和时间复杂度都优于Hybrid－TH。