网络计划，提高水利水电工程施工效率

项目五　网络计划的优化

通过绘制网络图，计算网络时间参数，以及确定关键路线，得到的仅是一个初步计划方案。为了得到一个从各方面都较好的方案，一般一项工程或任务的网络计划，往往要根据项目的要求综合考虑进度、资源利用和降低费用等目标，进行调整和改善，综合地考虑时间、资源和费用等目标，进行网络优化，确定最优的方案.

一、工期优化

欲对工程项目进行工期优化，必须抓住网络的关键路径，从各项关键活动中设法提出改进方案。关键路径上各工序如果拖期，就会影响整个工程的如期完成，若想压缩工程项目的完工期限，也必须从关键路径入手才能奏效，有时甚至要在初步网络图上修订几次才能达到要求。

（一）工期的调整和优化方法主要有：

（1）采取技术措施，主要是利用新技术、新工艺、高质量的原材料，或投入更多的人力、物力和设备，缩短工程完工时间。

（2）在工艺流程许可的情况下，对关键路线上的各道工序组织平行作业或交叉作业。

（3）采取组织措施，充分利用非关键工序的总时差，考虑放慢非关键工序的进度，合理调配人财物等资源去支援关键工序，缩短关键工序的作业时间。

（二）工期的调整步骤主要有：

（1）确定初始网络计划的计划工期和关键线路。

（2）将计划工期与指令工期比较，求出需要缩短的时间。

（3）采用适当的优化措施压缩关键线路的长度，并求出网络计划新的关键线路和工期。

（4）若调整后的工期符号规定要求，则优化结束，否则重复（3）直到符合要求为止。

【示例4－4】已知某工程双代号网络计划如图4－26所示，图中箭线下方括号外数字为工作正常持续时间，括号内数字为最短持续时间；箭线上方括号内数字为优选系数。压缩工作持续时间时，应将工作的优选系数（或组合优选系数，即优选系数之和）最小者作为优先压缩对象。现假设要求工期为15天，试对其工期进行优化。

【解】该网络计划的工期优化步骤如下：

（1）根据各项工作的正常持续时间，用标号法确定网络计划的计算工期和关键线路，如图4－27所示，此时关键线路为①——②——④——⑥。

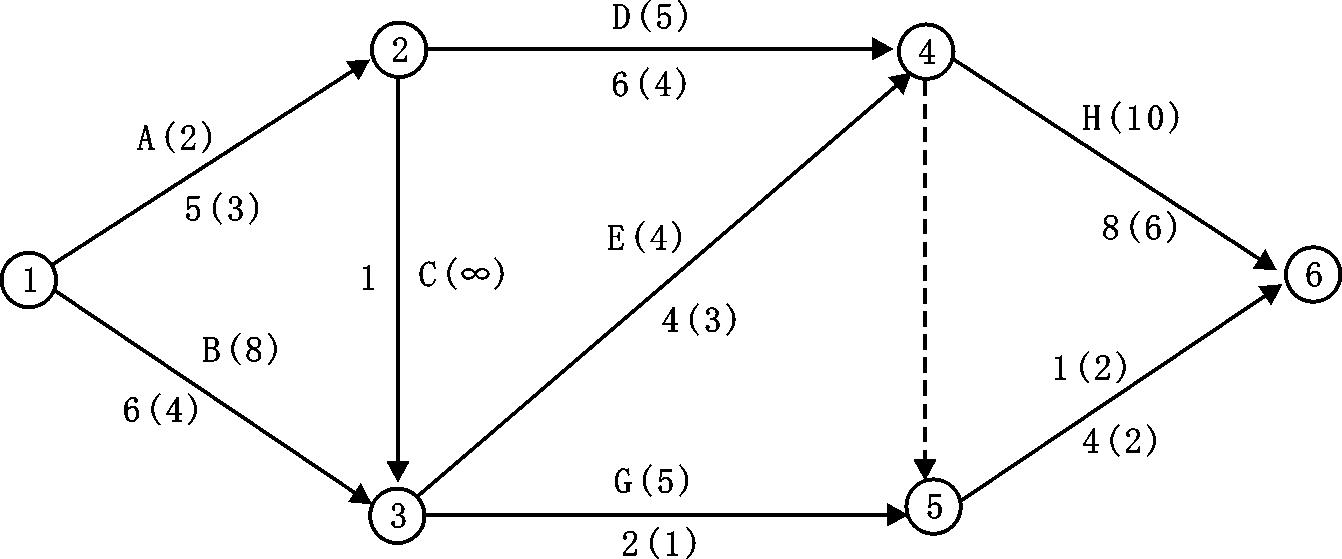
图4－26　初始网络计划

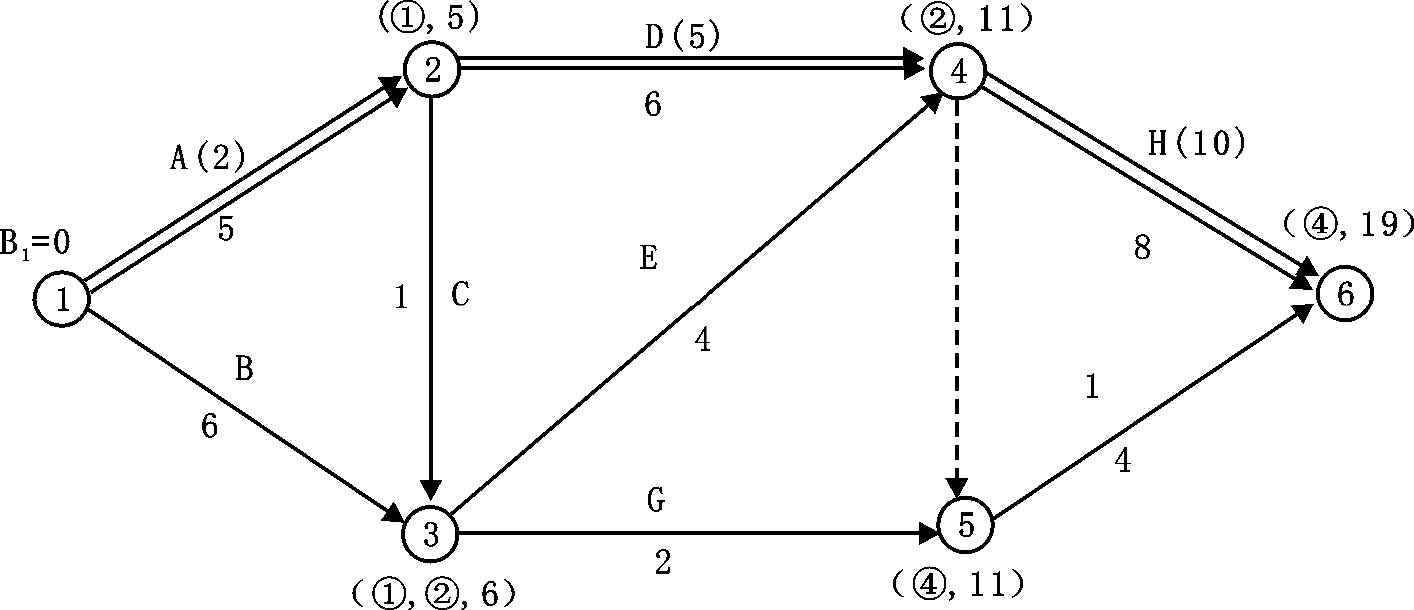
图4－27　初始网络计划中的关键线路

（2）计算应缩短的时间：

ΔT＝T_c－T_r＝19－15＝4

式中：T_c——网络计划的计算工期；

　　　T_r——要求工期。

（3）此时根据工作为：A、D和H，其中A工作的优选系数最小，因此应将A工作作为优先压缩对象。

（4）将关键工作A的持续时间压缩至最短持续时间3，确定新的计算工期和关键线路，如图4－28所示，此时关键工作A被压缩成非关键工作，故将其持续时间3延长为4，使之成为关键工作。此时，网络计划中有两条关键线路，即：①——②——④——⑥和①——③——④——⑥。如图4－29所示。

（5）此时计算工期为18，仍大于要求工期，故需继续压缩。在图4－29所示的网络计划中，有以下五个压缩方案：

①同时压缩工作A和B，组合优选系数为：2＋8＝10；

②同时压缩工作A和E，组合优选系数为：2＋4＝6；

③同时压缩工作B和D，组合优选系数为：8＋5＝13；

④同时压缩工作D和E，组合优选系数为：5＋4＝9；

⑤压缩工作H，优选系数为10。

图4－28　工作压缩最短时的关键线路

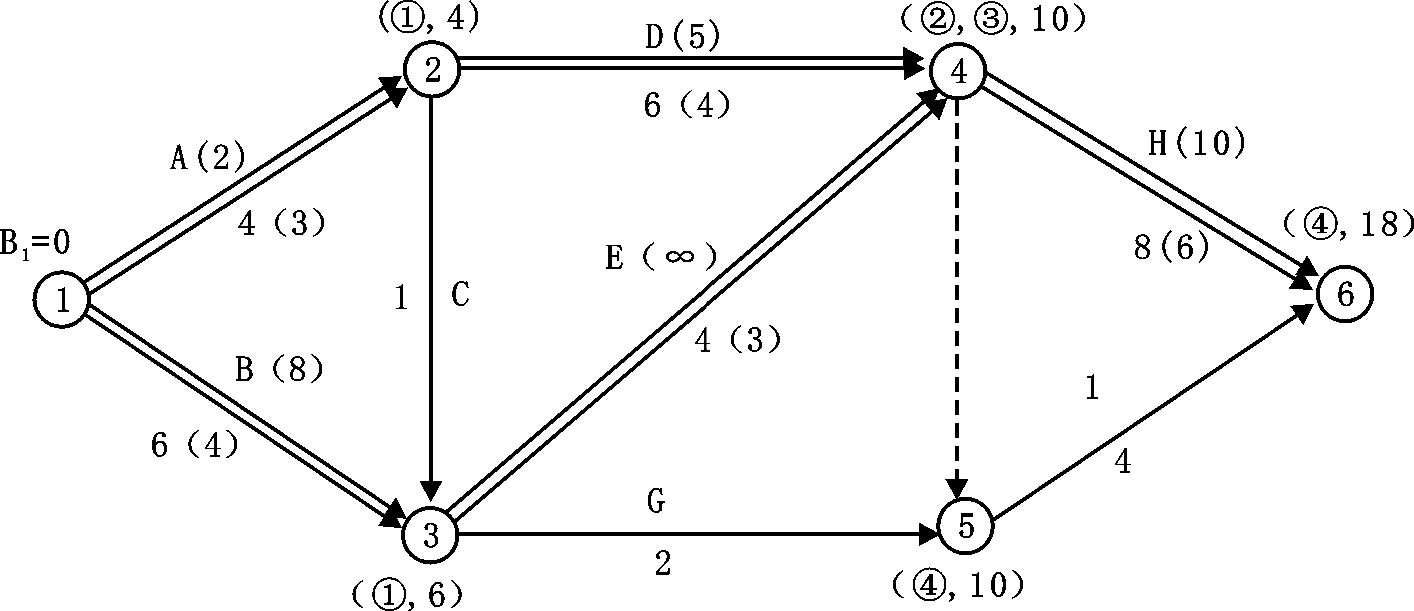
图4－29　第一次压缩后的网络计划

在上述方案中，组合优选系数最小的为方案②，故应同时压缩工作A和E，各压缩1天（压缩至最短），再确定计算工期和关键线路，如图4－30所示，此时，网络计划中仍有两条关键线路，即：①——②——④——⑥和①——③——④——⑥。

图4－30　第二次压缩后的网络计划

（6）此时计算工期为17，仍大于要求工期，故需继续压缩。由于关键工作A和E的持续时间已达最短，不能再压缩。故此时压缩方案只有两个：

①同时压缩工作B和D，组合优选系数为：8＋5＝13；

②压缩工作H，优选系数为10。

根据上述原则，应选择压缩工作H，将其持续时间缩短2，再确定计算工期和关键线路，如图4－31所示。此时计算工期为15，已等于要求工期，故图4－31所示网络计划即为优化方案。

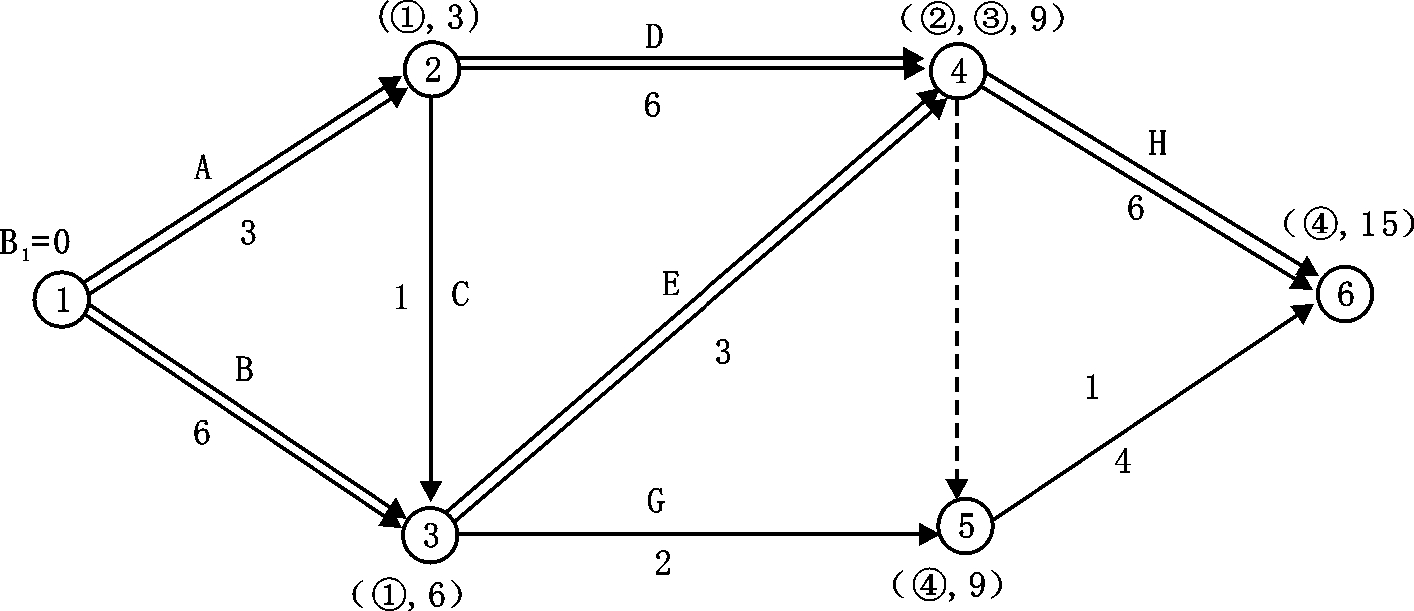
图4－31　工期优化后的网络计划

二、费用优化(www.xing528.com)

一项工程或计划都是由许多必要的工作或工序组礅的。这些工作或工序都有着各自的施工方法、施工机械、材料及持续时间等；根据这些因素和实际条件，一项工程可组合成若干方式。而成本就是确定最优组合方式的一个重要技术经济指标。但是，在一定范围内，成本是随着工期的变化而变化的，在工期与成本之间就应存在最优解的平衡点。工期－成本优化就是应用前述的网络计划方法，在一定约束条件下，综合考虑成本与工期两者的相互关系，以期达到成本低，工期短这样的平衡点的定量方法之不；

（一）时间—成本的关系

1.工程直接费用与间接费用的概念与关系

工程成本包括直接费用和间接费用两部分。在一定范围内，直接费用随着时间的延长而减少，而间接费用则随着时间延长而增加。曲线上的最低点就是工程计划的最优方案之一。此方案工程成本最低，相对应的工程持续时间称为最优工期。

间接费曲线：表示间接费用和时间成正比关系的曲线，通常用直线表示。其斜率表示间接费用在单位时间内的增加（或减少）值。间接费用是与施工单位的管理水平、施工条件、施工组织等有关。

直接费曲线：表示直接费用在一定范围内和时间成反比关系的曲线。一般在施工时为了加快作业速度，必须突击作业，也即采取加班加点和多班制作业，增加许多非熟练工人，并且增加了高价的材料及劳动力，采用高价的施工方法及机械设备等。这样，尽管工期加快了，但其直接费用也增加了。然而，在施工中存在着一个极限工期。另外，也同样存在着，不管怎样延长工期也不能使得直接费用再减少，此时的费用称为最低费用亦称正常费用。相应的工期称为正常工期。

直接费用曲线实际上并不像图中那样圆滑，而是由一系列线段组成的折线，并且越接近最高费用（极限费用），其曲线越陡。确定其曲线是一件很麻烦的事，而且就工程而言，也不需要这样精确，所以，为了简化计算，一般都将其曲线近似表示为直线。其斜率称为费用斜率：表示单位时间内直接费用的增加（或减少）。

根据各项工作的性质不同，其工作持续时间和费用之间的关系通常有以下两种情况：

（1）连续型变化关系

有些工作的直接费用随着工作持续时间的改变而改变。介于正常持续时间和最短时间（极限）之间的任意持续时间的费用可根据其费用斜率，用数学公式推算出来。这种时间和费用之的关系是连续变化的，称为连续型变化关系。

（2）非连续型变化关系

有些工作的直接费用与持续时间之间的关系是根据不同施工方案分别估算的，所以，介乎于正常持续时间与最短持续时间之间的关系不能用线性关系表示，不能通过数学公式计算，只能存在几种情况供选择。

根据优化循环的结果和间接费用率绘制直接费、间接费曲线。并由直接费和间接费曲线迭加确定工程成本曲线，求出其最佳工期最优成本。

间接费曲线根据已给的费用变化率（曲线斜率）和在极限工期时的值即可确定。将直接费曲线和间接费曲线对应点相加，即可得出工程成本曲线上的对应点。将这些点连接起来就得到工程成本曲线。从曲线上可以确定最佳工期：

2.网络计划时间—费用优化的步骤：

（1）按正常工期编制网络计划，并计算计划的工期和完成计划的直接费。

（2）列出构成整个计划的各项工作在正常工期和最短工期时的直接费，以及缩短单位时间所增加的费用，即单位时间费用变化率。

（3）根据费用最小原则，找出关键工作中单位时间费用变化率最小的工序首先予以压缩。这样使直接费增加的最少。

（4）计算加快某关键工作后，计划的总工期和直接费，并重新确定关键线路。

重复（3）、（4）的内容，直到网络计划中关键线路上的工序都达到最短持续时间不能再压缩为止。

（5）根据以上计算结果可以得到一条直接费曲线，如果间接费曲线已知，叠加直接费与间接费曲线得到总费用曲线。

（6）总费用曲线上的最低点所对应的工期，就是整个项目的最优工期。

三、资源优化

（一）资源优化的意义和目的：

1.意义

一项计划要按期完成往往会受到资源的限制，在实际任务的计划中，还需要考虑实现这项计划的客观物质条件。一项好的工程计划安排，一定要合理的使用现有的资源。如果工作进度安排的不得当，就会使正在计划的某些阶段出现对资源需求的高峰，而在另一些阶段则出现资源需求低谷。这种高峰与低谷的存在是一种资源没有得到很好利用的浪费现象。

2.目的

合理地安排工作进度，解决资源的供需矛盾或实现资源的均衡利用。

（二）资源优化的类型

1.工期限定，资源消耗均衡；

2.资源有限，工期最短；

（三）资源优化的方法

1.工期限定，资源消耗均衡

目标：在工期限定的条件下，安排工作进度，实现资源的均衡利用。

调整步骤：

（1）绘制时标网络图

（2）绘制资源图

（3）求资源高峰值Rm、平均值R平均、不均衡系数K

（4）调整各工序的开竣工时间，使物资供应均衡。

（5）计算调整后的资源高峰值Rm、平均值R平均、不均衡系数K，并与调整前进行比较。

2.资源有限，工期最短

目标：在资源有限的情况下，安排工作进度，力求使工期增加最少。

调整步骤：

绘制时标网络图；绘制资源需要量图；找出超过规定值的时间；调整相关工序的开竣工时间，使满足资源限制的条件，而工期又为最短。