工程图学基础教程：点的投影特征和坐标确定方法

3.1　点的投影

3.1.1　点在三面投影体系中的投影

如图3－1a所示，空间点A位于三面投影体系中，通过点A分别向H面、V面和W面作垂直投射线，则三条投射线与三个投影面的交点分别为点A在H面的投影a;在V面的投影a^'及在W面的投影a^″。a、a^'、a^″即为空间点A的三面投影。展开投影面体系后，如图3－1b所示。

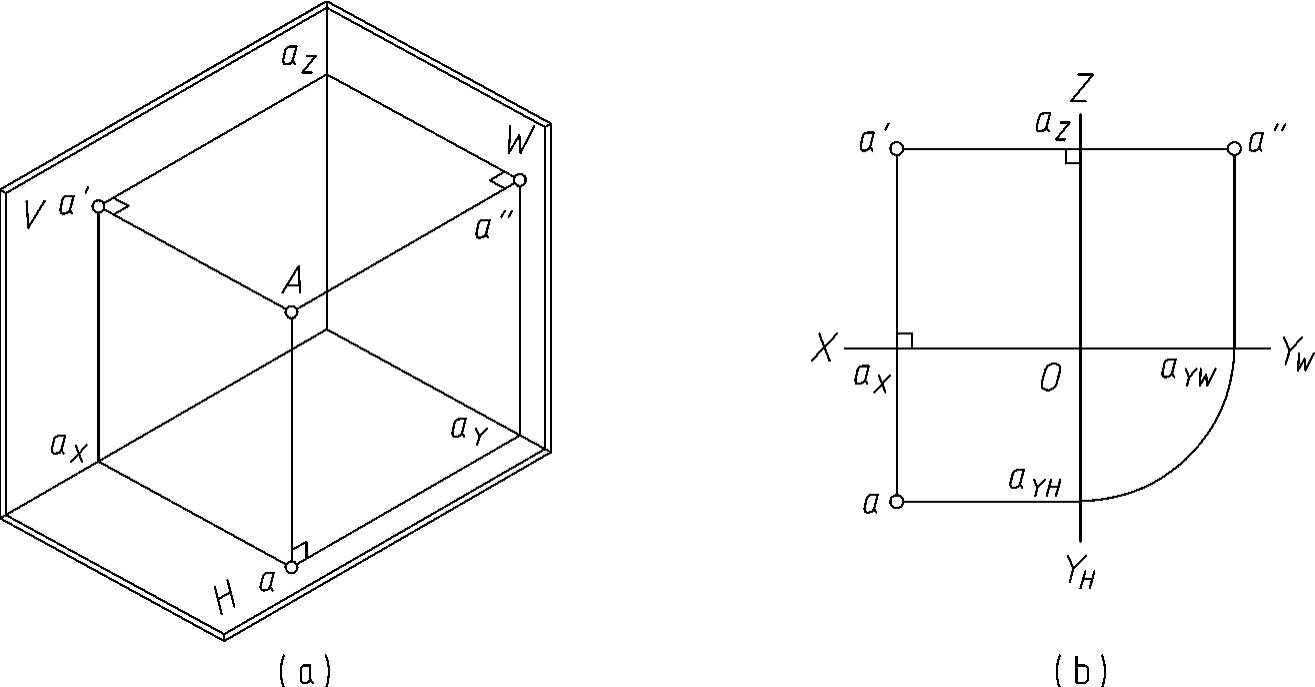
图3－1　点的投影

3.1.2　点的投影特征

在三面投影体系中，空间点用英文大写字母(如A、B、C…)表示，H面投影用小写 字母(如a、b、c…)表示，V面投影用相应小写字母并在右上方加一撇(如a'、b'、c'…)表示，W面投影用相应小写字母并在右上方加两撇(如a″、b″、c″…)表示。由图3－1b可知，点在三面投影体系中的投影特征如下所述。1.点的投影连线

1)点的水平投影a与正面投影a'的连线垂直于OX轴，即aa'⊥OX。

从图3－1a可看到Aa⊥H面，Aa'⊥V面，故由Aa与Aa'构成的投射平面Aaa_Xa'既⊥H面又⊥V面。因为该三面相互垂直，其交线也相互垂直，故有a'a_X⊥OX，aa_X⊥OX。当展开投影面时，a'a_X不动，aa_X以a_X为圆心，绕OX轴向下旋转90°与V面重合，因此有aa'⊥OX。

2)点的正面投影a'与侧面投影a″的连线垂直于OZ轴，即a'a″⊥OZ。

证明与上类似，从略。2.点的投影到投影面的距离1)点的正面投影a'到OX轴的距离等于点的侧面投影a″到OY_W轴的距离，即为空间点A到H面的距离，即a'a_X=a″a_YW=Aa。因为Aaa_Xa'是一矩形，其对边平行相等，故aa_X=Aa';a'a_X=Aa。2)点的水平投影a到OX轴的距离等于点的侧面投影a″到OZ轴的距离，即为空间点A到V面的距离，即aa_X=a″a_Z=Aa'。3)点的水平投影a到OY_H轴的距离等于点的正面投影a'到OZ轴的距离，即为空间点A到W面的距离，即aa_YH=a'a_Z=Aa″。由上可知，点到某一投影面的距离等于点在另两投影面上的投影到相应投影轴的距离。

例3－1已知点A的水平投影a及正面投影a'，求作点A的侧面投影a″(图3－2a)。分析根据点在三面投影体系中的投影特征:a'a″⊥OZ;aa_X=a″a_Z，即可求得a″。作图1)过a'作OZ轴的垂线。2)量取aa_X=a″a_Z，a″即为所求，如图3－2b所示。用图3－2c、d、e所示的三种方法也可求得同一结果。

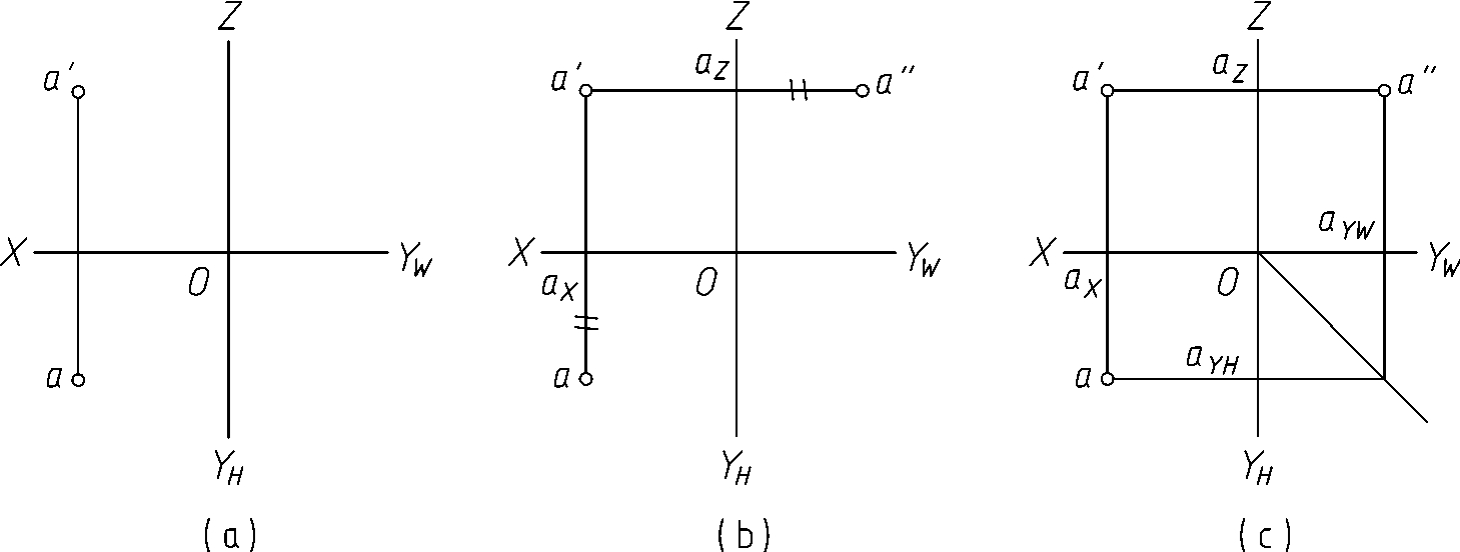
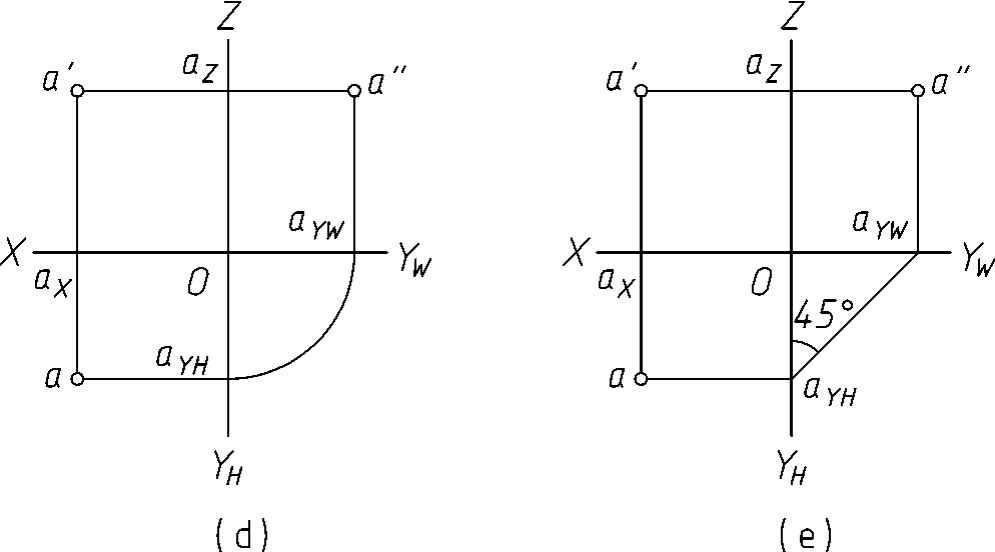
图3－2　已知点的两面投影求第三投影

3.1.3　特殊位置的点(www.xing528.com)

当点距某一投影面的距离为零时，该点便在此投影面内。图3－3a中点B即为H面内的点。其水平投影与其本身重合，正面投影在OX轴上，侧面投影在OY_W上，其投影如图3－3b、c所示。

当点距两投影面的距离均等于零时，则表明该点在投影轴上。如图3－3a所示的点C，即为OX轴上的点，其水平投影与正面投影均与其本身重合，侧面投影在坐标原点，如图3－3b、c所示。

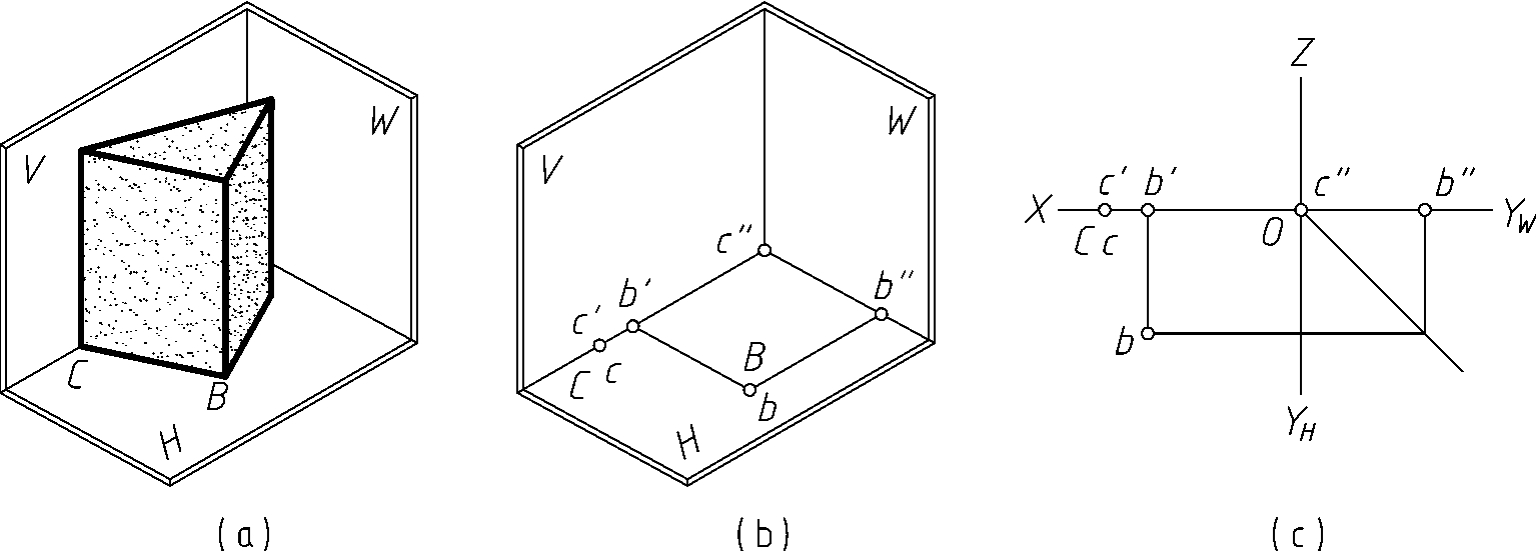
图3－3　投影面内的点

3.1.4　点的投影与点的坐标

空间点的位置可由它的三面投影确定。另外，从解析几何可知，点可以在直角坐标系中确定，如果把投影体系看成坐标系，把投影面看成坐标面，把点到投影面的距离用坐标值来表示，则点的空间位置便可以用坐标方式表达。

将点表示为A(X，Y，Z)，括号外为点的名称，用大写英文字母表示，括号内用数值表示点的对应坐标值，即可给定点的空间位置。

例3－2已知C(3，2，4)，求作点C的三面投影(图3－4a)。

分析已知点C的坐标值，即知点到投影面的距离，则有C_c″=X=3，C_c'=Y=2，C_c=Z=4。

作图

1)分别在OX轴上定Oc_X=3，在OY_H及OY_W上定Oc_YH=Oc_YW=2，在OZ轴上定Oc_Z=4;

2)再分别过c_X、c_YH、c_YW、c_Z作相应轴的垂线，各垂线的交点为c、c'、c″，即点C的三面投影。

由图3－4b可看出:c由X、Y坐标确定，c'由X、Z坐标确定，c″由Y、Z坐标确定，说明点的每个投影，可由点的两个坐标确定。所以，只要给出点的两个投影，便可完全确定点在空间的位置。因此，利用两面投影也可表示几何元素或形体的投影。

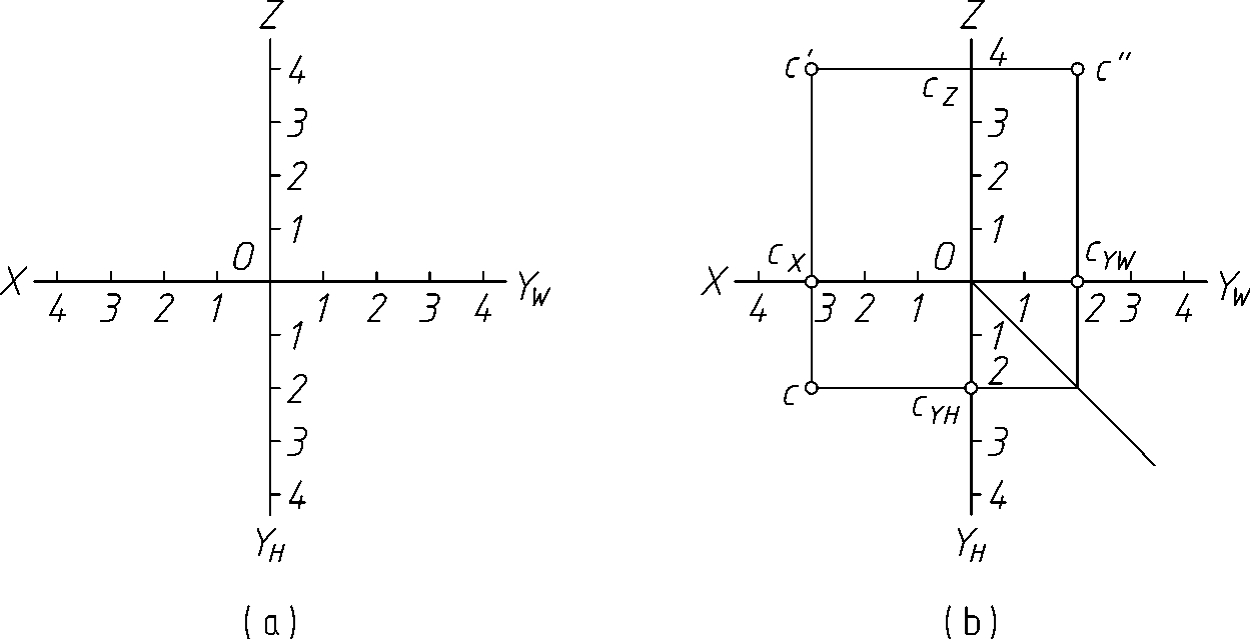
图3－4　已知点的坐标值求点的投影