三个悖论解决方案-当代中国人文大系

三、主要的悖论解决方案

1.关于“解决方案”的要求

早在欧洲中世纪，经院逻辑学家们就对悖论问题进行了深入、细致且有洞察力的研究。他们当时把悖论称之为“不可解问题”（insolubles），主要研究以说谎者悖论为主体的语义悖论的各种变形，如前面提到的“转圈悖论”和“砝码悖论”，并且还讨论了认识论悖论，即与知道、相信、怀疑、犹疑这类认识论概念以及真假这类语义概念相关的悖论；语用悖论，即与命令、答应、允诺或希望这一类指导行动的话语或态度有关的悖论，如某人颁布了唯一一道命令:“不执行这道命令！”被命令人究竟是执行还是不执行这道命令？中世纪逻辑学家们还提出了各种各样的悖论解决方案，威尼斯的保罗在他的书中一口气就列出了15种之多。主要的观点有:（1）拒斥:一个悖论不是命题，因为它不能被称之为真的或假的，是无意义的。（2）限制:悖论源自于自我指称，而对自我指称应采取各种方法予以限制，因为它是非法的。（3）解析:悖论是有意义的真正的命题，并且确实是自我指称的，但它们都是假命题。（4）区分悖论性命题的普通涵义和精确涵义，这已初步接触到语言分层次的思想。

各种集合论悖论特别是罗素悖论的发现，触发了所谓的“第三次数学危机”，悖论受到高度重视，提出了各种各样的悖论解决方案。大致可以把这些方案分为两类:一类是对悖论持否定态度，认为悖论是思维“患病”的征兆，是思维中的矛盾，应该根据我们现有的逻辑祛除或避免，下面要谈到的公理集合论、罗素的类型论、塔斯基的语义学、克里普克的真理论等都可归入此列。另一类是对悖论持肯定态度，认为悖论是人的思维所不能避免的，它甚至有某种本体论和认识论的依据，因此正确的方法是承认悖论的合法性，然后对我们已有的逻辑做某种修改，后面要谈到的次协调逻辑就属于此列。后一类解决方案是晚近才出现的。

随着各种悖论解决方案的出现，对悖论的何种解决是合适的解决这一问题也提出来了。罗素可能最先考虑这一问题，他认为一个悖论解决方案应至少满足三个条件:（i）让悖论消失；（ii）尽可能让数学保持原样；（iii）非特设性，即此方案的提出除“能避免悖论”这一理由之外，应有其他的理由。 ⁽¹⁵⁾苏珊·哈克曾在概括罗素等人论述的基础上，对悖论解决方案提出了更明确的要求。一方面，从形式或技术上说，这种方案应提供一套相容或一致的语义学或集合论理论，用以表明那些导致悖论的看上去无懈可击的前提或推理原则必须被拒斥。并且，这种形式理论还应满足下述要求:不应如此宽泛以致损害了本应保留的推理（“不要因厌恶脸而割掉鼻子”原则，克林曾把它概括为:“治病但不应治死人”）；但它又要足够宽泛以堵住相关的悖论性论证，以免悖论重新产生（“不要跳出煎锅又入火坑”原则）。另一方面，从哲学上说，这种方案应说明为什么导致悖论的那些前提或推理看上去是无懈可击的，而实际上却必须被拒斥。 ⁽¹⁶⁾不过，也有人不同意这些意见，特别是“非特设性”这一条，例如冯·赖特认为，矛盾律和排中律是思维的基本规律和最高准则。假如使用某个短语或词去表示、指称某个事物导致矛盾，这就是不能如此使用这个词或短语的理由；假如从某个悖论性语句或命题能够推出矛盾，这就是该语句或命题不成立的理由。他通过对说谎者悖论和非自谓悖论的详细分析，指出:“悖论并不表明我们目前所知的‘思维规律’具有某种疾患或者不充分性。悖论并不是虚假推理的结果。它们是从虚假前提进行正确推理的结果，并且它们的共同特征似乎是:正是这一结果即悖论，才使我们意识到（前提的）假。” ⁽¹⁷⁾

下面对几种主要的悖论解决方案作一简单讨论。

2.公理集合论的解决

对罗素悖论的分析表明，它是基于如下几个前提或假定之上的:（i）素朴集合论中的概括原则，即任一性质F（x）决定一个集合S；（ii）对任一集合S，S∈S是一有意义的命题；（iii）任一集合S可作为元素属于另外的集合S′或属于S自身；（iv）一阶逻辑是集合论的基础逻辑。由这四个前提，可推出康托尔悖论赖以产生的另两个前提:（i）存在大全集，即有由一切集合组成的集合；（ii）由任一集合可以生成其幂集，即由该集合的所有子集构成的集合。一般认为，作为集合论的基础逻辑的一阶逻辑是不可动摇的，于是要摆脱悖论，就只能至少否定前三个前提或假定之一。两种集合论公理系统ZF（C）和GB（C）分别作出了不同的选择，ZF（C）否定（i），对集合的生成作出更严格的限制；BG（C）否定（ii），对集合元素的身份作出更严格的限制。

ZF（C）是在1908年策梅罗系统的基础上，经斯柯伦、弗兰克尔、冯·诺伊曼等人的改进和补充所建立的一个公理化系统，是对素朴集合论的形式化处理。其核心做法是修改原来的概括规则:并非由任一性质都能决定一个集合，而只能在已经形成的集合中由任一性质能够分离出一新的集合。这一思想体现在分离公理模式和正则公理中。ZF（C）系统的初始概念是集合和属于关系，有以下十条公理:外延公理、空集合存在公理、无序对集合存在公理、并集合公理、幂集合公理、无穷公理、分离公理模式、替换公理模式、正则公理（亦称基础公理）和选择公理（记为C）。 ⁽¹⁸⁾这里把与处理悖论相关的两个公理详述如下:

分离公理模式 对任一集合x和任一集合论公式A（z），都存在另一集合y，y的元素恰好由x中所有那些满足公式A（z）的元素构成，即

正则公理 对任一非空集合x，都存在另一集合y，使得y∈x但y与x不相交，即

由于采用这些公理，康托尔悖论和罗素悖论所赖以产生的那种大全集不再出现，由此避免了悖论。

BG（C）是冯·诺伊曼于1925年提出的系统，后经贝尔纳斯、哥德尔修改而成。这个系统的创立者认为，悖论产生的真正根源不在于使用了过大的集合，而在于让这些过大的集合再作为其他集合或它自身的元素。因此，有必要对做集合元素的资格作出更严格的限制，具体做法是:不修改概括规则，而区分集合和真类，前者可以作为其他集合的元素，而后者则不能再作为其他集合的元素，由此摆脱悖论。BG（C）系统的公理分为五组:A组公理，4个；B组公理，有关真类存在的8个公理；C组公理，有关集合存在的4个公理；D组公理，类似于ZF（C）中的正则公理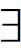；组公理，即选择公理，但比ZF（C）中的选择公理稍强。 ⁽¹⁹⁾后来证明，BG（C）是ZF（C）的保守扩充，即ZF（C）的定理都是BG（C）的定理，但BG（C）中涉及真类的那些定理不是ZF（C）的定理。我们将这一结果称为这两个系统的准等价性。

从技术上说，ZF（C）和BG（C）作为避免悖论的方案是成功的，但问题在于是否需要对它们做哲学辩护。按前面所谈到的罗素、苏珊·哈克等人的意见，是需要做这种辩护的，因为可以对这些系统的背景假定提出质疑，如它们在公理的选择上存在任意性、特设性，公理本身有真假对错问题，这些系统本身有一致性或可靠性问题，而按哥德尔不完全性定理，最后一个问题只有在比这些系统更强的系统中才有答案，因此只能获得相对的解决。按另一些人的意见，这些系统能够避免悖论，并且能够做现有的数学，这就是对这些系统的最好辩护。

3.罗素的类型论

在解决悖论方面，罗素作过多种不同的尝试，如曲折理论、限制大小理论、无类或非集合理论等，其中影响最大的是类型论。 ⁽²⁰⁾从技术上说，它所否定的是罗素悖论赖以产生的前提（iii）:任一集合S可作为元素属于另外的集合S′，或者属于S自身；从哲学上说，它的基础是前面引述过的“恶性循环原则”:没有一个整体能够包含只能借助于这个整体才能定义的元素。类型论分为简单类型论和分支类型论。

在简单类型论中，每一个集合都有一个确定的层次；一集合x能够是另一集合y的元素，当且仅当y的层次比x的层次恰好多1；层次为0的对象被称为个体，或者被称为原子或本元。在这一理论中，变元都带有层次:对于每一正整数n，都有n层变元x_n和y_n等，它们表达n层对象。于是，这一理论中就没有不附加层次类型（简称型）的对象，人们不能泛泛谈论所有的对象如何，而只能谈论某一层次的所有对象如何。并且，在这一理论的语言中，对于任一变元x_i和y_j，x_i∈y_j是合式公式当且仅当j＝i＋1。因此，当某一对象的型并不比某一集合的型恰好小于1时，说那个对象是该集合的元素，不仅是错误的，而且是无意义的。通常把如此构成的简单类型论系统称为T，T除一阶逻辑的公理和推理规则之外，还包括外延公理、概括公理、乘法公理和无穷公理。 ⁽²¹⁾

简单类型论不能排除像里查德悖论这样的语义悖论，罗素由此发展了分支类型论。它把同一型的集合再分为不同的层次，高层次的集合不能再被当作低层次的集合看待。最低层次的集合被称为“直谓的”，决定它的性质或谓词也被称为直谓的性质或谓词，其他层次的集合或性质被称为“非直谓的”。例如，一个n＋1型集合S_n＋1，如果对于任一n型对象x_n，必须考察n＋1型整体方能断定x_n是否属于S_n＋1时，则称S_n＋1是非直谓的。非直谓的层次是高的，根据概括公理，由任一性质可决定一集合，于是非直谓的集合可借由定义它的性质来说明。使用罗素原来的例子，“一个典型的英国人具有大多数英国人所具有的性质”，这里“具有大多数英国人所具有的性质”也是一种性质，但它涉及个体性质的全体，是一个非直谓的性质。一般地说，凡涉及某一类型的全体而又是此类型的性质的性质，叫做非直谓性质；否则，叫做直谓的性质。体现上述思想的分支类型论系统记为RT，它是由对T中的概括公理做某种限制而得到的。RT可以避免语义悖论，但所付出的代价却相当严重。对于一个集合，人们不能笼统地说此集合的所有元素（它们是较低型的集合）都有某种性质，而必须区分层次才能作出断定。实数就是这样的一个集合，于是对实数就不能作出一个单一的断定。这样一来，分支类型论就不能作为描述数学命题的恰当工具。为了弥补这一严重缺陷，罗素又给RT引入了还原公理:每一非直谓性质都有一直谓性质与之等价。这就等于取消了直谓和非直谓的区分，也就取消了分支类型论。

一般认为，类型论在哲学上的问题就是它的特设性，它禁止任何形式的“恶性循环”，也就是禁止任何形式的自我指称或自我相关。但如前所述，并非一切形式的循环都是恶性的，也并非一切形式的自我指称都导致悖论，有不少循环或自我指称的命题相当自然，且丝毫不会导致悖论，例如，“本语句不是用斜体字印刷的”，“数1是使得对一切数x而言都有x×1＝1的数”。更有人这样断言:若禁止一切形式的循环或自我指称，则会牺牲掉大部分数学，或至少是使得许多数学表述极其复杂、笨重和繁琐。

4.塔斯基的语义学

塔斯基在《形式化语言中的真概念》 ⁽²²⁾一文中指出，当把前一章中说到的T模式

T　X是真语句当且仅当p

应用于日常语言时，会导致悖论。他转述了乌卡谢维奇给出的一个导致悖论的描述。令符号C是“C不是一个真语句”这一语句的缩写，于是我们有:

（α）“C不是一个真语句”等同于C。(www.xing528.com)

然后对语句C的那个带引号的名称，提出T模式的具体说明，即

（β）“C不是一个真语句”是一个真语句，当且仅当，C不是一个真语句。

从前提（α）和（β），立刻就得到一个悖论:

（γ）C是一个真语句，当且仅当，C不是一个真语句。

塔斯基通过分析后发现，悖论的产生有两个原因:一是日常语言的普遍性，又称“语义封闭性”，即这种语言不仅包含它的句子及其他表达式，而且包含了这些句子和表达式的名称，以及包含这些名称的句子，并且还包含了像“真的”、“假的”、“指称”、“外延”这样的语义表达式。二是通行的逻辑推理规则在其中成立。塔斯基认为，为了避免悖论，我们显然不能抛弃通行的逻辑推理规则。他于是把矛头指向日常语言的普遍性或语义封闭性，并作出结论说:这种普遍性是造成一切语义悖论的根源；要在一个如此丰富、普遍的语言系统内无矛盾地定义真概念是不可能的。

于是，塔斯基指出，一个可接受的真定义应该满足两个限制条件:一是实质的充分性或内容的适当性，一是形式的正确性。一个真定义是实质上充分的，是指它能够把T模式的所有特例作为后承推演出来，凡不能衍推T模式的所有特例都不能作为真定义，例如“X是真的当且仅当（在《圣经》中断定）p”就不能作为真定义，因为它不能推出“‘布什于1988年当选为美国总统’是真的，当且仅当（在《圣经》中断定）布什于1988年当选为美国总统”。由此可知，T模式并不是真的定义，它本身只是无穷多的语句的一个模式，至多算作“真的”部分定义，只有T模式的所有特例的逻辑合取才能作为“真的”完全定义。实质充分性条件唯一确定了词项“真的”外延即适用范围，因此每个实质上充分的真定义都必定与实际构造的定义相等值。

真定义的形式正确性包括下述要求:（1）必须区分语言的层级，即区分被谈论的语言和用来进行这种谈论的语言，前者是对象语言，后者是元语言。真定义必须相对于一定的语言层次，例如“在对象语言O中真”只能在元语言M中才能得到定义，而“在元语言M中真”则只能在元元语言M′中才能得到定义。（2）这两种语言都必须具有“明确规定的结构”，即都必须用公理化、形式化的方法来表述:首先给出不加定义的初始词项，给出造词、造句的规则（形成规则），通过定义引入其他词项；其次给出与初始词项相关的公理和推理规则，并经过证明程序得到定理或可证语句。由此保证两种语言中的每一个表达式在形式上都可唯一地确定，避免歧义和混淆。（3）元语言必须比对象语言“实质上更丰富”，这就是说，元语言必须把对象语言作为一个真部分包括在自身之内，此外它还包括:对象语言的表达式的名称，如其引号名称或结构摹状名称；通常的逻辑工具，如“并非”、“或者”、“并且”、“如果，则”、“当且仅当”之类的逻辑词项；适用于对象语言句子的语义表达式，如“真的”、“假的”、“满足”、“有效”等。不过，由于这些语义词项并不是足够清晰以至可以安全使用的，所以它们不能作为初始词项，而只能通过严格的定义引入。借用逻辑类型论的术语，元语言必须具有比对象语言更高类型的变元。

塔斯基区分了两种形式的语言:一类是“较贫乏的”，即其元语言真正丰富于对象语言，元语言具有比对象语言更高的逻辑类型；一类是“较丰富的”，即其对象语言和元语言中的变元具有相同的逻辑类型，以至元语言中所有的词项和语法形式都能在对象语言中得到翻译。对于这两类不同的形式语言，塔斯基得到了两个不同的结果:（1）对于前者，无矛盾地给出实质上充分、形式上正确的真定义是可能的。他相对于类演算（作为对象语言），并使用一个形式化的元语言，给出了他的真定义。用这种办法，摆脱或避免了语义悖论。（2）对于后者，要给出这样的定义而不导致矛盾（悖论）是不可能的；他具体相对于形式算术系统证明了这一点，这就是著名的真的不可定义性定理。

与罗素的类型论一样，塔斯基的语义学也含有禁止恶性循环或自我指称的意蕴，只不过罗素通过在对象语言内部分类型和层次来实现这一点，而塔斯基则通过语言本身的分层和使语义概念“真”、“假”相对化来实现这一点。塔斯基方案影响很大，但同样面临很多非议，主要是这样几点:（1）强烈的特设性。塔斯基给语言分层并使“真”、“假”概念相对化的唯一理由就是:如果不这样做，则会导致悖论。但这套做法却与我们的日常语言习惯和直觉相冲突，因为我们日常所使用的只是同一个语言，并不像塔斯基所说的那样使用“语言1”、“语言2”……“语言n”等；我们也只分别使用一个有确定意思的“真”、“假”概念，并不像塔斯基那样使用“真1”、“真2”……“真n”等。（2）实际操作时的不可行性。克里普克给出了这样的例子:迪安说，“尼克松关于水门事件所说的一切话都是假的。”假如尼克松关于水门事件所说的话中恰好包含这样一句话:“迪安关于水门事件所说的一切话都是真的。”根据塔斯基理论，前一句话应该处于比尼克松关于水门事件所说的话更高的层次，而后一句话应该处于比迪安关于水门事件所说的话（包括前一句话）更高的层次，那么，这两句话究竟谁比谁的层次高？实际上我们根本无法确定，而从这两句话可以导出矛盾。（3）语义封闭性的要求太强。许多后来的研究者都认为，语义封闭的语言不一定导致悖论，有些研究者还使用不同的技术，构造出包含自身的真定义的一致的语言。亨迪卡和他的学生桑朵在他们所构造的IF逻辑中就做到了这一点。 ⁽²³⁾（4）语言层次的终结问题。在塔斯基的语言分层体系中，前一层次语言的语义概念只能在后一层次的语言中才能得到严格的说明，但问题在于:这个分层体系是否终结于某个统一的元语言？如果没有这样的一个元语言，则所有分层次的语言的语义概念都没有一个最后的支撑点，其可靠性没有最终的保证；如果有这样一个元语言，则它就是一个语义封闭的语言，其中是否会像在其他语义封闭的语言中一样出现悖论？正因为如上所述的一些原因，我们不能说塔斯基理论已成功地解决了悖论。

5.克里普克的真理论

正是由于对塔斯基的理论不满意，克里普克于1975年发表重要论文《真理论纲要》 ⁽²⁴⁾，其中发展了一种新的真理论以及以此为基础的悖论解决方案。他运用克林尼的强三值逻辑模型，用严格的形式手段发展了此前有人（例如马丁和伍德努夫）已提出过的一种观点:只存在一个真谓词，它可以用于含有这个谓词的语言本身，但这种语言不会导致悖论，其办法是通过允许真值空缺并使悖论性语句处于这种空缺之中来避免悖论。这套理论的核心概念是“有根性”、“固定点”和“真值空缺”。一个语句是有根的，当且仅当，可以通过一定的程序把它的真值归结为某个先前语句的真值，或者说通过某个先前的语句是否为真来确定它是否为真。一个含有多个叠置的真谓词的语句是有根的，当且仅当最终可以通过这种程序把它的真值归结于某个不含真谓词的语句的真值。例如，要确定“‘‘‘树叶是绿的’是真的’是真的’是假的”的真值，我们就要依次确定“‘‘‘树叶是绿的’是真的’是真的’”、“‘‘树叶是绿的’是真的’”的真值，最终要依据经验确定“树叶是绿的”这个语句的真值。这样的本身不含真谓词而可以凭借某种经验的或逻辑—数学的手段确定其真值的语句称为该语言的一个“固定点”。有固定点的语句才是真正有根的，否则称为“无根的”。无根的语句是悖论性的，它们在含有关于自身的真谓词的该语言的任何固定点中都既不真也不假，而是处于真值空缺之中。克里普克方案的优越之处在于，它不仅仅停留在单纯的哲学思辨之上，而是用严格的逻辑技术手段把相应的哲学思辨构造成一个形式化理论，从而使它具备了可理解性、可批判性和可比较性。

正如有的论者所指出的，克里普克的这个方案与塔斯基的相比，的确在某些方面更符合直观。他所主张的有根性观念以及只需有一个真谓词的要求都是有道理的。不过，他所提出的内里分层的语言虽然含有它自己的真谓词，却并不是一种无所不包的语言，它还需要一种没有真值空缺的元语言。更具体地说，（i）他对极小固定点的归纳定义是在一个集合论语言中而不是在该对象语言本身中给出的。（ii）有些关于对象语言的断定不能在该对象语言中给出。例如，“本语句是假的”在该对象语言中不是真的，但我们无法在该对象语言中说“‘本语句是假的’不是真的”。（iii）由于“有根性”（以及“悖论性”）都不属于该对象语言，因此像“本语句是假的或无根的”这样的强化的说谎者悖论就无法用他的理论来解决。克里普克自己也承认:“必须上升到一个元语言也许是本理论的一个弱点。塔斯基层次的幽灵依然与我们同在。”这样一来，他的理论与塔斯基的相比，就没有根本的差异。 ⁽²⁵⁾

6.某些新近的发展

已有的各种解决悖论的方案在总体上之不太成功，在学术圈内逐渐滋长了另一种倾向，即转而对悖论持肯定态度，认为悖论也许是我们的思维甚至是外在世界中固有的，是我们永远摆脱不掉的。对于悖论，正确的态度也许不是拒斥它，而是学会与它相处；当出现矛盾或悖论时，更合理的办法也许是让它们留在理论体系，但把它们“圈禁”起来，不让它们任意扩散，危害我们所创立或研究的理论整体，使它们成为“不足道”的。这种观点显然与认为矛盾律至高无上的经典逻辑不相容，与传统的真理观也不相容。于是，有些研究者选择了比较激进的途径:修改传统的真理论，修改不允许任何矛盾、主张从矛盾可以推出任意命题的经典逻辑。这方面有代表性的理论是赫兹伯格的“素朴语义学” ⁽²⁶⁾，普里斯特等人所倡导的“次协调逻辑”（paraconsistent logic） ⁽²⁷⁾。例如，在所谓的“次协调逻辑”中，能够容纳有意义、有价值的“真矛盾”，但这些矛盾并不能使系统推出一切，导致自毁。因此，这些新逻辑具有一种次于经典逻辑但又远远高于完全不协调系统的协调性。 ⁽²⁸⁾

次协调逻辑家们认为，如果在一理论T中，一语句A及其否定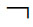A都是定理，则T是不协调的；否则，称T是协调的。如果T所使用的逻辑包含有从互相否定的两公式可推出一切公式的规则或推理，则不协调的T一定是不足道的。因此，通常以经典逻辑为基础的理论，如果它是不协调的，那它也就一定是不足道的。这一现象表明，经典逻辑虽可用于研究协调的理论，但不适用于研究不协调但足道的理论。巴西逻辑学家达·科斯塔在20世纪60年代创立次协调逻辑，构造了一系列次协调逻辑C_n（1≤n≤w），以用作不协调而又足道的理论的逻辑工具。对次协调逻辑系统C_n的特征性描述包括下述命题:

（1）矛盾律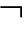（A∧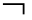A）不普遍有效；

（2）从两个相互否定的公式A和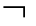A推不出任意公式；即是说，矛盾不该在系统中任意扩散，矛盾不等于灾难。

（3）应当容纳与（1）和（2）相容的大多数经典逻辑的推理模式和规则。

上述（1）和（2）表明了对矛盾的一种相对宽容的态度，（3）则表明次协调逻辑对于经典逻辑仍有一定的继承性。

在任一次协调逻辑系统C_n（1≤n≤w）中，下述经典逻辑的定理或推理模式都不成立:

若以C₀为经典逻辑，则系列C₀，C₁，C₂，…，C_n，…，C_ω使得对任正整数i有C_i弱于C_i－1，C_ω是这系列中最弱的演算。已经为C_n设计出了合适的语义学，并已经证明C_n相对于此种语义是可靠的和完全的，并且命题逻辑系统C_n还是可判定的。

次协调逻辑在形式上可能说得过去，问题在于其哲学方面。鉴于矛盾律在我们的思维和科学理论构造方面的中心作用，修改矛盾律或限制它的作用范围，必须给出充足的理由；以往解决悖论的方案在某些方面有缺陷，并不是可以转而承认悖论为所谓的“真矛盾”的充足理由。我将在后面进一步阐明这一点。