经典逻辑中的逻辑真-当代中国人文大系

二、经典逻辑中的逻辑真

前已指出，命题是真值承担者，那么什么是逻辑真的承担者？回答是“命题形式”。所谓命题形式，是指为表达不同思维内容的各种命题所共同具有的结构方式，它是各个不同命题抽去具体内容后只保留其位置的框架，或者说，是由这些位置和联结它们的成分形成的结构。所以，命题形式一般有两种成分:代表具体内容的位置和组合这些位置的成分，分别叫做变项和逻辑常项。变项是命题形式中的内容要素，逻辑常项则是命题中的结构要素，后者规定着命题形式的类别。命题有具体内容，因而有真假；命题形式抽象掉了命题的具体内容，只剩下逻辑内容即形式结构，因而无真假可言。但是，由于逻辑常项相当于某种函数运算或计值规则，当给定一命题形式中诸变项的值或真值之后，其中所含逻辑常项就会派生出该命题形式的真值。从这个意义上，命题形式具有派生的真值。特别地，当用具体的词项或命题分别取代一命题形式中的全部变项后，得到该命题形式的一个代入例，或者说一个解释。命题形式的代入例或解释是一个具体的命题，自然有真假。同一个命题形式，经过不同的代入或解释，可以得到不同的命题。一般地，一命题形式可以有无穷多个解释。如果一命题形式在任一解释下都真，则称为永真式，如“所有S是S”，“p或者非p”，“如果xRx，则xRx”。如果一命题形式在任一解释下都假，则称为永假式，如“所有S都不是S”，“p且非p”，“（x）（（xRy）∧（xRy））”。如果一命题形式在有些解释下真，则称为可满足式，如“所有S都是P”，“如果p且q，则r”，“如果（x）F（x），则F（y）”。一命题形式永真，亦称逻辑真；一命题形式永假，则称逻辑假。由此可见，真假是命题的性质，而逻辑真（永真）、逻辑假（永假）、可满足则是命题形式的性质，两者之间有明显的区别。在哲学中，常常把一真命题叫做“真理”；同样，在逻辑中我们也可以把一永真的命题形式叫做“逻辑真理”。

现在的问题是:究竟什么是逻辑真理？如何在逻辑或哲学上对它予以严格的说明和刻画？

许多哲学家和逻辑学家从各种不同角度对逻辑真理进行了探讨，提出了各不相同的逻辑真定义。例如，莱布尼茨最先明确区分了逻辑真理和事实真理。他说:“有两种真理:推理的真理和事实的真理。推理的真理是必然的，它的否定是不可能的；事实的真理是偶然的，它的否定是可能的。” ⁽⁷⁾他又把推理的真理直接称为必然真理，把事实真理直接称作偶然真理，并认为必然真理的依据是矛盾律，在所有可能世界中真；偶然真理要遵守充足理由律，在有的可能世界中真。莱氏所定义的推理真理是比较宽泛的，不仅包括狭义的逻辑真理，而且还包括数学和其他必然为真的真理。维特根斯坦则认为:“逻辑的命题是重言式”，它们没有排除任何可能的情况，对于其中所含基本命题的一切真值可能性都是真的。“逻辑命题的特殊标志是，它的真值是从符号本身得知的，这个事实包括一切逻辑哲学。非逻辑命题的真值或假值是不能单从这些命题认出的，这也是极其重要的事实。” ⁽⁸⁾卡尔纳普相对于某个语义系统，用两种方式定义了语句的L真:

C1　语义系统S1的一个语句A是L真（即逻辑真）的，当且仅当A在S1中的真只建立在S1的一些语义规则上，无需参照任何事实。

C2　语义系统S1的一个语句A是L真的，当且仅当A在所有状态描述中都可满足，即A的域是所有状态描述所组成的类。

上述各种定义都有这样或那样的问题。例如，维特根斯坦把逻辑真理等同于重言式，这实际上假定了所有逻辑命题都能够归约为真值函项演算的命题。而这一假定是大成问题的，因为它相当于逻辑演算的判定问题是可解的。丘奇等人已经证明判定问题对于所有演算并不是一般可解的，例如形式算术系统的判定问题就是不可解的。王浩指出，维特根斯坦在这里犯了两个错误:一是混淆或者说抹杀了有穷和无穷的区别，另一个是过于理想化的假定:基本命题是彼此独立的。他说，按照维氏的标准，甚至一阶逻辑也不是逻辑真理。这显然是大成问题的。 ⁽⁹⁾

蒯因与其说是一位有哲学兴趣的逻辑学家，毋宁说是一位有逻辑背景的哲学家。出于其逻辑和哲学的双重需要，他对逻辑真理的定义、性质和特征等作了长期探讨和系统说明。早在1936年发表的论文《根据约定的真》中，他就对逻辑真理提供了说明，其中起关键作用的是词项的本质出现和空的出现。“一个词语在一个陈述中可以说有本质出现，如果用另一个词语替换该词语就能使该陈述变成假的。” ⁽¹⁰⁾例如，在陈述“约翰是诗人或者不是诗人”中，“或者”一词有本质出现，因为若将它换成“当且仅当”，就得到一明显为假的矛盾陈述。而“约翰”、“诗人”的出现不是本质性的，因为将它们分别换成“汤姆”、“哲学教授”之后，所得到的陈述仍为真。“一个表达式可以说成空虚地出现于一给定陈述内，如果用任一语法上可允许的表达式替换它之后，而使该陈述的真或假毫无改变。”给出上述解释之后，逻辑真理可以定义如下:“如果S″只含有逻辑表达式的本质出现，因而当除开逻辑表达式的那个构架之外，一切东西都以语法上可能的所有方式改变之后，它仍保持为真，则S″的真就只依赖于那些逻辑构成要素，并因此是一逻辑真理。” ⁽¹¹⁾

在《卡尔纳普和逻辑真理》（1954）一文中，蒯因重复了上述定义:“首先我们假定，假如没有别的办法，就通过枚举指出，哪些词语可以叫做逻辑词；典型的是‘或者’、‘并非’、‘如果’、‘那么’、‘并且’、‘所有的’、‘每一个’、‘只有’、‘有的’。于是，逻辑真理就是那些只包含逻辑词语的本质出现的真语句。这意味着:任何其他的词语，尽管也出现在一逻辑真理中，例如‘布鲁斯特’、‘杀死’和‘凯撒’出现在‘布鲁斯特杀死凯撒或并未杀死凯撒’中，却能够随意改变，而不会使语句变为假的。” ⁽¹²⁾在《经验论的两个教条》（1951）这篇著名论文中，蒯因也指出:“一般地说，一个逻辑真理就是这样一个陈述，它是真的，而且在给予它的除逻辑常项以外的成分以一切不同的解释的情况下，它也仍然是真的。” ⁽¹³⁾

所有这些定义都是基于先已定义的“真”、“假”概念之上的，并且都预先假定了一个逻辑词语或者说逻辑常项的清单，而后者只能通过枚举给出。蒯因指出，借助于真这个普遍概念，再加上对一特定语言的逻辑词语的完全枚举，我们就可以定义逻辑真理概念。“一旦给定了逻辑词语，我们就有办法在真理这个属之下清楚地区分出逻辑真理这个种。” ⁽¹⁴⁾循此思路，在他的《逻辑哲学》一书第四章中，蒯因给出了五个近乎等价的逻辑真定义。 ⁽¹⁵⁾

（i）根据结构为真。蒯因说:“我把一个逻辑真语句定义为其真是为它的逻辑结构所担负的句子。无论如何，为了避免误解，最好还是把它更清楚地表述为这样:一个句子逻辑上为真，如果具有它的逻辑构造的所有句子皆为真。”而这里所说的句子的逻辑结构是指它的真值函项、量词和变元方面的组成。按照我们已经接受的标准语法，对于一语句来说，所存在的一切就是逻辑结构和谓词。只要把模式字母“F”、“G”等放在一个句子中谓词的位置上，就已经描述了它的逻辑结构。例如，（x）（Fx∧Fx）就体现了一类语句的逻辑结构。蒯因认为，如此定义逻辑真理概念之后，就可以由它得出逻辑上重要的其他概念:一个句子逻辑上为假，只要它的否定逻辑上为真；两个或两个以上的句子逻辑上不相容，只要它们的合取逻辑上为假；一个句子逻辑上最终蕴涵另外一个，如果它同另外一个的否定不相容。由此又可定义出“等值”:互相蕴涵的句子是逻辑上等值的。

（ii）根据替换为真。蒯因指出:既然一语句中除开逻辑结构之外就是它的谓词，因而可以把逻辑真更简单地定义为:“一个句子逻辑上为真，只要对于它的谓词的所有改变，它都保持为真。”这里所说的谓词的所有改变，按照狭义的理解，是指用任意一个另外的谓词替换其中的某个或某些谓词，例如在

中，用“溶解”去替换“飘动”，得到:(www.xing528.com)

若按广义理解，谓词的所有改变实际上是指用含其他谓词的语句去替换含原谓词的简单句。例如，在（1）中用“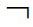（x燃烧）”去替换“x飘动”，得到:

于是，逻辑真又可定义为:“一语句在逻辑上为真，如果用语句对它的简单构成句作替换后，其结果总是真语句。”这里的限制条件是:替换必须是一律的，即必须在被替换成分出现的一切场合用同一语句去替换。上面的（3）是一逻辑矛盾，因而是假的，而它是由（1）通过替换得到的，所以根据逻辑真的替换定义，（1）不是逻辑真的。

（iii）根据模型为真。蒯因说，在（ii）中是用替换去定义有效性，实际上也可以利用集合论去定义它，不过要借助于两个初等概念:一是逻辑模式的集合论类比，一是模型。前者是指集合论中的某种开语句，我们可以采用下列方法从逻辑模式中得到它:我们把诸如“Fx”、“Fy”、“Gx”等的谓述加以改变，把它们读成“x∈α”、“y∈α”、“x∈β”等，由此导致“α”、“β”之类的变元，它们的值乃是集合。我们借助于有序偶来处理二元谓词字母，即把“Hxy”改读为“〈x，y〉∈γ”。对于三元谓词字母或更多元的字母做相应的处理。例如逻辑模式“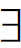（x）（Fx∧Gx）”把开语句“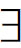（x）（x∈α∧x∈β）”作为它的集合论类比。这个句子谈论集合，并引来了量词“（α）”、“（β）”等，而模式字母“F”和“G”只是模拟谓词，根本不是有值的变元。这个模式是一个样本，它描述了某些句子的逻辑形式；另一方面，它的集合论类比却又是具有那种逻辑形式的实际句子，它是一个开语句，为某些集合的实例而不是为别的东西所满足。而一个模式的模型是集合的一个系列:每一集合对应于该模式中每一模式谓词字母；而且，作为一集合序列的初始集合，非空集合∪（全集）构成变元x，y等的值域。在模型中，对应于一元模式谓词字母的集合就是∪的各元素所构成的集合，对应于二元模式谓词字母的集合就是∪的元素有序偶所构成的集合，如此等等。简单地说，如果一模型满足特定模式的集合论类比，则我们说它满足该模式。更完整的表述:当我们把一模型的其他集合都分别指派给集合变元“α”、“β”等时，模式的集合论类比为真，则可以说该模型满足该模式。这时，有效性的新定义可这样表示:一个模式是有效的，如果它被它的所有模型所满足；而逻辑真语句则是通过在一个有效的模式中作替换而可能取得的任何句子。

逻辑真定义（iii）和（ii）的一个显著差别是:（ii）所讨论的是语句的一切替换，而（iii）说的是集合的一切指派。由于并非每个开语句都决定一个集合，并且并非每个集合都被一个语句所决定，因而逻辑真的替换定义和模型定义是不同的。但是，只要对象语言丰富到足以谈论初等数论，这两个定义就是等价的。因为一个模式对于初等数论的语句的所有替换为真，当且仅当它被每个模型所满足。

（iv）根据证明程序为真。蒯因注意到，以上三种定义都预先假定了真概念，而后者超出了对象语言的范围。他寻求在对象语言内定义逻辑真，而不必依赖于真概念。他利用了哥德尔的谓词逻辑完全性定理:

（B）如果一个模式被每个模型所满足，它就能够被证明。

蒯因说，我们可以简单地描述构成这些完全性证明程序之一的步骤，然后把一有效模式定义为被这些步骤证明了的模式，这样我们就可以把一逻辑真理定义为用这些证明规则所导出的任何句子。他的意思也许是说:选择一些明显地逻辑真的句子，并运用从公式变换到公式且保持逻辑真的形式规则，所能得到的都是逻辑真命题。在经典谓词演算中，有不同的等价方法，可以用来证明这一点。

如果对于蒯因观点的上述理解是正确的话，那么我认为，上述定义中存在逻辑循环，并且达不到他不借助真概念直接定义逻辑真的目的。因为要证明由一证明程序得出的任何句子都逻辑真，我们至少要证明，出发命题即公理都逻辑真，并且推理规则保持逻辑真，这些都需要事先定义好了的逻辑真概念。当然，如果我们已经证明一个逻辑系统的可靠性和完全性（两者合称广义完全性），我们就可以安全地把它的定理集与逻辑真理集相等同:凡能被它证明的都是逻辑真的，凡逻辑真的都能被它证明。不过，这至多可以算作对逻辑真理的一种描述，不能算作对它的定义。

（v）根据语法为真。蒯因指出，只要假定对象语言在谓词方面足够丰富，前四种定义在外延上是等同的，它们断定了同样的语句为逻辑真；并且，它们都依赖于对象语言中的三种语法构造:否定、合取和量化，只不过有的定义明确提到这些构造，有的隐含地涉及而已。蒯因认为，我们还可以借助于某个对象语言中可能包含的任何语法构造，而不特别借助于否定、合取和量化，去更加抽象地定义逻辑真。按照这种方法，一逻辑真语句就是凡具有其语法结构的句子皆真的语句。当语句之间可以通过词汇替换而相互转换时，它们便具有相同的语法结构。我们对逻辑真的新定义于是可以这样提出:一逻辑真语句就是在对其词汇作替换时不可能变为假的语句。当我们用任何属于同一语法范畴的别的符号串来替换它的词汇成分时，所得到的那个句子为真。

在蒯因的新定义中，逻辑结构概念让位于语法结构概念，词典和语法之间的对比取代了逻辑词汇和非逻辑词汇的截然二分。由于词典和语法是相对于某一语言而言的，因此蒯因所提出的关于逻辑真的抽象定义，不仅仅依赖于这一语言，而且还依赖于我们如何把它语法化。并且，这一新定义还涉及逻辑与语法之间一种值得注意的联系:一旦我们确定了关于一个语言的两样东西，即它的语法和它的真谓词，则它之中哪些句子算是逻辑真理也就被确定了。所以蒯因指出:“用机械学的术语来说，逻辑是语法和真这两大部件的合成物。”

实际上，逻辑真概念还可以得到更精确的形式刻画，这就是“有效性”概念。在经典逻辑中，逻辑真理和有效公式两个概念是相互重合的:凡逻辑真理都是有效公式，凡有效公式都是逻辑真理，只不过“逻辑真理”是一个直观概念，而“有效公式”则是一个形式概念，它是前者的精确化。我们在前面第五章关于“形式系统的解释”的讨论中已经给出了“有效性”（逻辑真）概念的精确定义。