当代中国人文大系：真理论的逻辑构造简析

一、真理论的逻辑构造

一般而言，逻辑并不直接研究或确定一简单命题的真假，而是在假定简单命题的真假之后，去研究这些命题及其复合命题之间的真假关系:当一个或一些命题真时，另一个或另一些命题是否为真？但是，逻辑毕竟要涉及到简单命题的真假，这在命题逻辑语义中表现为:首先假定任一原子公式必取且只取真、假二值之一；在一阶逻辑语义中，首先确定原子公式F（t₁，…，t_n）在赋值σ下的值:如果F是一阶语言的一个n元非逻辑谓词符号，t₁，…，t_n都是项，那么

σ（F（t₁，…，t_n））＝1，当且仅当，σ（t₁），…，σ（t_n）＞∈（F）^σ

这里1代表真，0代表假。有些逻辑学家如塔斯基首先制定关于真的逻辑定义，再在此基础上给出关于逻辑真的定义。所以，在讨论逻辑真理概念之前，有必要先从逻辑角度简单讨论一般真理观的一些问题。

1.真值承担者

所谓真值承担者，就是能够为真或为假的东西。问题是:究竟谁是真值承担者？是语句（sentence）？陈述（statement）？命题（proposition）？抑或是判断（judgment）？

语句有广义和狭义之分。广义的语句即语言学中的语句，它是一种语言单位，由某种语言内的语词或词组按一定的语法规则组成，其特点在于:合乎语法规则，具有明确的意思。这种意义的语句包括陈述句、疑问句、祈使句、感叹句四种类型。狭义的语句除具有上述特点外，还必须能够作为真值承担者，即（1）必须或者肯定或者否定；（2）必须或者真或者假。这种意义的语句只包括陈述句、某些特殊的疑问句（如反诘句）以及特殊的感叹句。很多现代逻辑学家常在狭义上使用语句概念。

“命题”一词有两种主要用法，其中最常见的是把它理解为语句的涵义，即由一语句表达的具有主体间性的思想内容，能够为真或为假。于是，语句和命题就是一种表达和被表达的关系。若广义地理解语句，则（i）所有命题都由语句表达，但并非所有语句都表达命题，例如疑问句、祈使句、感叹句一般不表达命题，因为它们没有真假可言；（ii）不同语言的不同语句，甚至同一语言中的不同语句，可以表达同一命题；（iii）由于词汇歧义、结构歧义、指示性短语以及语境等因素，同一语句可以表达不同的命题。若狭义地理解语句，则所有命题都由语句表达，且所有语句都表达命题。

“陈述”一词有时指说出或者写出某个或某些语句的动作或行为，如陈述案情，陈述自己的观点等；有时作为名词，表示说出或写出一个陈述或似陈述句（反诘句和某些感叹句）时所述说的东西，即由这些句子所表达的思想内容。在这个意义上，“陈述”几乎与“命题”同义。

判断就是被实际断定为真或为假的命题。对于同一命题，人们可以采取不同的态度，如断定、相信、猜测、反驳、询问、怀疑等，这些都是对命题的态度，简称“命题态度”（propositional attitudes）。举例来说:

张三去关门。

张三去关门？

张三去关门！

这三个句子分别具有陈述、建议、命令这三种态度。顺便说一下，命题的另一种涵义就是:用不同语气说出或写出几个句子时所共同表达的东西，如上面三个句子中所表达的“张三关门”。在奥斯汀和塞尔等人的言语行为理论中，一般用FA表示以言行事行为，其中的A即是命题，F表示命题态度。

判断与命题的区别在于:命题未必经过断定，被断定了的命题才是判断。例如，哥德巴赫猜想“每一个大偶数都可以表示为两个素数之和”就是一命题，本身有真假，但究竟是真是假，尚未被证明，尚未被断定，所以只是命题，不是判断。因此，判断除具有命题的两个特征，即或者肯定或者否定，或者真或者假之外，还有第三个特征:或者被断定为真或者被断定为假。由于判断与一定的断定者相关，是因断定主体而异的，例如一位数学家的知识库与一位农民的知识库有共同的交集，但不交的部分远远大于交的部分；还由于判断涉及断定和非断定，具有心理主义色彩，在弗雷格之后几乎被弃置不用。

综上所述，语句是一种可见可闻的物质性客体，而命题、陈述、判断则是心智性的东西，它们由语句表达，但不能被归结为语句，而是人们在听到或见到一个语句时所理解的东西。用图表示:

在语句、命题、陈述、判断这四者中，似乎谁都可以作真值承担者。谁是本来意义上的真值承担者？谁是派生意义上的真值承担者？哲学家、逻辑学家们对此众说纷纭，意见不一。例如，弗雷格认为语句是真值承担者，蒯因进一步认为，并不是一般的语句，而是他所谓的恒久句（eternal sentence），即永远为真或永远为假的语句，它们的真假与凑巧说出或书写出它们的特定环境无关。但有些哲学家不赞成把语句作为名称，并把语句的真值当作它的所指的做法。他们认为，不是语句直接为真为假，而是语句所表达的思想即命题为真为假。例如，“你欠我10美元”这类语句之所以没有固定真值，时而为真，时而为假，是因为它在不同情况下表达了不同的命题，其真值不固定是它所表达的命题不固定造成的。假如它所表达的命题确定，则其真值也确定。因此，不是语句本身而是语句所表达的命题才是真值承担者。他们指出，倘若语句确有所指的话，其所指也不是真值，而是某个事物状态，简称事态（state of affairs）或事实（fact）。如果语句所描述的事态存在，则它所表达的命题为真；如果它所描述的事态不存在，则它所表达的命题为假。因此，命题是真值承担者，语句在下述意义上获得派生的真值:根据它所表达的命题的真或假而成为真的或者假的。

我赞同“命题是本来意义上的真值承担者，语句则是派生意义上的真值承担者”的说法。不过，在明确命题和语句的上述区别之后，为使用方便计，在日常实践中我们常常把这两者等同使用，但并不会造成严重的混乱。

2.符合论和塔斯基的真定义

关于真理，至少可以区分出两个问题:一是真理的定义和说明问题，即说一语句或命题为真是什么意思？二是真理的检验和识别问题，即凭借何种方法、途径和标准去断定语句或命题的真？通常认为有五种主要的真理论:符合论、融贯论、实用论、冗余论和语义论。我们这里只简单考察符合论，并把语义论视作实现符合论的一种技术性构造。塔斯基自己就曾指出过，真的“语义学概念只不过是古典概念（亚里士多德的符合论——引者）的一个现代形式” ⁽³⁾。

符合论的基本思想是:语句的真不在于它与其他语句的关系，而在于它与客体、与世界的关系，在于它与客体在世界中的存在方式或存在状况的符合与对应。与有关客体的事实相符合的语句为真，不符合的为假。这种符合论有两个基本前提:（1）存在着独立于心灵的实体，它们是主体认识的对象。假如没有与思想对立的这类实体，符合和对应就失去了赖以比较的基础。（2）人的认识能够达到客体。假如人的认识永远达不到客体，那也就不存在人的认识是否符合客体的问题，“相符合”因此变得毫无意义。所以，符合论是真理的一元论，它以实在论和可知论为前提。

符合论具有悠久的传统，其起源一直可追溯到古希腊的亚里士多德。在现代，罗素、早期维特根斯坦、奥斯汀及绝大多数逻辑实证主义者，都是符合论的倡导者和坚持者。符合论最合乎人们的常识和直观，但它在理论上也存在许多困难，例如它的三个关键性概念——命题、事实和符合，特别是后两者，就未得到明确的阐释，经不起深入的推敲。并且，根据思维与之相符合的对象是绝对理念、物质世界、感觉经验等，符合论还可以区分出不同的形态。符合论并不一定就是唯物主义的认识论和真理论。

1933年，塔斯基发表了一篇重要论文《形式化语言中的真概念》，“它的任务是，相对于一个给定的语言，建立一种实质上充分和形式上正确的关于‘真句子’这个词项的定义” ⁽⁴⁾。塔斯基认为，这个定义应该把握亚里士多德关于真的直觉:

说是者为非，或说非者为是，是假的；

说是者为是，或说非者为非，是真的。(www.xing528.com)

他将其用精确的符号公式表示出来，得到著名的T模式:

T　　X是真语句当且仅当p

这里p可用“真的”这个词适用于它的任何句子代替，而X则可由这句子的名称代替，其名称可以是引号名称，也可以是结构摹状名称。下面是T模式的一个著名的例子:

“雪是白的”是真的当且仅当雪是白的。

塔斯基发现，当把T模式应用于日常语言时，却会导致悖论。为了避免悖论，一个可接受的真定义应该满足两个限制条件:一是实质的充分性或内容的适当性，一是形式的正确性。 ⁽⁵⁾他相对于类演算（作为对象语言），并使用一个形式化的元语言，给出了满足这两个要求的真定义。蒯因在他的《逻辑哲学》（1970）一书的第一章中，相对于一阶谓词演算，使用英语加对象语言作元语言，定义了真概念，其真定义与塔斯基的真定义本质上是相通的。苏珊·哈克在她的《逻辑哲学》（1978）一书的第七章中基本上按蒯因方法表述了塔斯基的真定义。由于一阶谓词演算是更为人熟知的，其技术性符号也比类演算更少，相对于这种对象语言作出的真定义也就更好理解。因此，我们下面以蒯因和哈克的表述为蓝本，说明塔斯基关于真概念的定义。

塔斯基定义真概念的程序包括以下步骤:（1）规定对象语言O的语法结构，真谓词是相对于O而被定义的；（2）规定元语言M的语法结构，其中“在O中真”将得到定义；（3）在M中定义“在O中满足”；（4）在M中根据“在O中满足”定义“在O中真”。

塔斯基之所以通过“满足”来定义“真”，是因为他考虑到，复合的闭语句并非直接由原子闭语句构造而成，而是由语句函项（亦称开语句）构造而成。例如，（x）（Fx∨Gx）就是由开语句Fx和Gx通过析取和存在量化构造出来的。而开语句Fx和Gx并不是真的或假的，而只是被对象满足或不满足。例如，雪满足开语句“x是白的”，而煤不满足它。塔斯基的主要思路是:他通过递归方法来定义“满足”，即先给出那些最简单的语句函项被满足的条件，再给出复合语句被满足的条件。最后，他把闭语句当作语句函项的一种特例（自由变元数为0的语句函项），同时把“真”当作“被满足”的一种特例，由此给出他的真定义。

在塔斯基那里，满足是开语句与对象的n元有序组之间的关系。对象的n元有序组是由n个对象组成并带有次序关系的集合，以二元有序组〈x，y〉为例，〈x，y〉并不等于〈y，x〉，就像“x＞y”不同于“y＞x”一样。因此，次序关系对于有序组是至关重要的，〈x，y〉＝〈z，w〉当且仅当x＝z并且y＝w。如上所述，开语句本身并不真或假，只为对象的n元有序组所满足或不满足。例如，“x走”为每一个行走的动物所满足，但不为任何无生物所满足；“x＞y”为有序二元组〈5，3〉所满足；“x在y和z之间”为有序三元组〈廊坊，北京，天津〉所满足。从理论上说，开语句中可以含有1，2，3……直至任意多个自由变元，于是塔斯基把有序n元组扩充成为对象的无穷序列，“满足”成为开语句与某种约定下的无穷序列之间的关系。例如，开语句F（x₁，…，x_n）便为〈a₁，a₂，…，a_n，a_n＋1，…〉这个序列所满足，因为该开语句被该无穷序列中的前n个元所满足，至于序列中的其他后继元a_n＋1，…，可忽略不计。例如，“x征服y”就被头两个元素是凯撒和高卢的任意无穷序列〈凯撒，高卢，…〉所满足，而不论其后继元是什么。

以上说明了原子开语句的满足，复合开语句的满足由原子开语句的满足来定义。开语句S的否定为所有不满足S的序列所满足；S₁和S₂的合取为那些既满足S₁又满足S₂的序列所满足；而带存在量词的开语句为一对象序列所满足，当且仅当，存在另一序列，该序列至少在第i位上与前一序列不同，其中第i个元是由存在量词所约束的变元，该序列满足由带存在量词的开语句删掉量词后所得到的开语句。换一种方式说，一存在量化开语句为一对象序列所满足，当且仅当，其构成语句为某个至多除第i位以外与该序列相同的序列所满足。以（y）（x征服y）为例。此开语句为一对象序列所满足，当且仅当“x征服y”为一个至多除第二位外与该序列相同的序列所满足。于是，如所希望的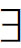，（y）（x征服y）为第一个元是凯撒的每一个序列所满足，这是因为“x征服y”为其第一、第二个元分别是凯撒和高卢的每一个序列所满足。再如，（x）（x是位于y和z之间的城市），为序列〈保定，北京，郑州，…〉所满足，因为该语句去掉量词后得到的语句“x是位于y和z之间的城市”，为序列〈石家庄，北京，郑州，…〉所满足，当然也为序列〈保定，北京，郑州，…〉所满足，这三个序列的差别至多只在约束变元x所在的位置上出现。

下面根据“满足”来定义“真”。闭语句是其中变元都被量词所约束，因而不含自由变元的语句，它是开语句的一个特例，即零元开语句。一序列的第一个元及其所有后继元都与该序列是否满足一零元开语句无关。因此，塔斯基便把一闭语句为真定义为被所有序列所满足，一闭语句为假定义为不被任何序列所满足。例如，二元开语句“x是y的妻子”便为所有形如〈邓颖超，周恩来，…〉的序列所满足，一元开语句“x是作家”为所有形如〈鲁迅，…〉的序列所满足，而不管其后继元是什么。同理，零元开语句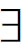（x）（x是一名老师）为所有形如〈…，…，…〉的序列所满足，无论其第一元和其他后继元是什么，因为存在一个序列如〈孔子，…〉，它至多与其他任意序列在第一元上不同，它满足开语句“x是一位老师”，后者是由（x）（x是一名老师）删掉量词后得到的。

一个闭语句要么真要么假，因而它要么为所有序列所满足，要么不被任何序列所满足，它不能只被某些序列所满足，而不被某些另外的序列所满足。为什么要这样定义“真”和“假”？考虑一个例子:（x）（x是一座城市）。令X是一个任选的对象序列，根据关于存在量化的满足定义，X满足这个闭语句，当且仅当，存在某个另外的序列Y，它至多与X在第一个元上不同，并且它满足由该闭语句删掉量词后的开语句“x是一座城市”。既然对象a满足“x是一座城市”意味着a是一座城市，所以若存在某个对象是城市，则一定存在一个如上所述的对象序列Y。于是，若有某个对象是城市，则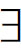（x）（x是一座城市）为所有序列所满足。

下面给出塔斯基型真定义的形式表述。

蒯因选择了一个极为俭省的一阶语言作为对象语言O，除它的初始符号中包括存在量词“”而不包括全称量词“”，而本书第四章所述的一阶语言L包括全称量词“A”而不包括存在量词“”外，两者在其他方面是相同的，故将对象语言O的细节略去，直接给出有关“满足”和“真”的定义。

Ⅰ.“满足”的定义

令X，Y是任意的对象序列，A，B是对象语言O中的任一语句，X_i表示任意对象序列X中的第i个元，var（i）表示字母表中的第i个变元。

（i）对任意一元谓词F，任i和X，X满足为var（i）所跟随的“F”，当且仅当X_i是F。

（ii）对任意二元谓词G，任i和X，X满足为var（i）和var（j）所跟随的G，当且仅当X_i和X_j有G关系。

（iii）对其他n元（n≥3）谓词，任i和X，可类似定义相应语句的满足。

（iv）对任意序列X和任意语句A，X满足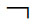A当且仅当X不满足A。

（v）对任意序列X和任意语句A，B，X满足A∧B当且仅当X满足A并且X满足B。

（vi）对任意序列X，Y，任意i以及任意语句A，X满足A关于var（i）的存在量化，当且仅当，存在某个另外的序列Y，使得对任意j≠i都有X_j＝Y_j，并且Y满足A。

Ⅱ.“真”的定义:对象语言O中的一闭语句为真，当且仅当它被所有的序列所满足。

关于他的真定义，塔斯基着重强调了以下几点:（1）这个定义不仅是形式上正确的，而且是实质上充分的，即能推出T模式的所有特例。（2）从这一定义可以推演出各种普遍性定律，尤其是矛盾律和排中律——后两者完全足以表达亚里士多德的真概念的特征。（3）将此定义应用于数学中相当大一类领域的形式语言中，可以获得更进一步的重要结果。例如，对于足够丰富的形式系统来说，其真谓词是不能无矛盾加以定义的。塔斯基具体证明了:算术中的“真句子”概念不能在一阶算术中定义。这就是著名的真不可定义性定理，它与更为著名的哥德尔不完全性定理可以互推。（4）从有关真概念的讨论中所得到的大多数结论，经过适当改变后都可以扩展到其他语义学概念上去，如满足，指示，定义，推论或后承，同义，意义等，对其中每个概念都可按我们分析真概念所使用的方法进行分析。 ⁽⁶⁾