当代中国人文大系：dere模态与本质主义

四、dere模态和本质主义

在模态谓词逻辑中，容许有这样的公式:

这两个公式甚至是许多模态谓词逻辑系统的公理。但□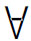（x）F（x）和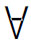（x）□F（x）是很不相同的:在□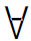（x）F（x）中，模态词置于量词之前，不在量词的辖域内，它修饰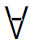（x）F（x）整个语句（所谓的de dicto模态），不会使后者中的约束变项出现指称晦暗性。而在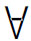（x）□F（x）中，模态词在量词的辖域内，它所修饰的是F（x），使其中的约束变元具有指称晦暗性（所谓de re模态）。简单地说，de dicto模态是加于命题之上的算子，由已有的命题形成新的命题；而de re模态则是加于命题谓词之上的，由已有谓词形成一个新谓词，模态词是这个新谓词的一部分。它们两者之间有原则性区别。

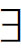例如，□（x）F（x）是de dicto模态，（x）□F（x）则是de re模态。蒯因用一个例子说明这两者具有不同的真值:在一种不容许不分胜负的博弈中，参加者有一个人将获胜是必然的，即□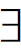（x）F（x）为真；但是，不存在这样一个参加者，使得人们可以说他获胜是必然的，即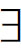（x）□F（x）为假。再如，BF的前件说:所有的x必然是F；而它的后件说:“所有的x是F”是必然的。用可能世界语义学的话来说，BF的意思是:如果在世界w_i中的所有x在w_i可通达的所有可能世界w_j中是F，则在世界w_i可通达的所有可能世界w_j中所有x都是F。这是要求在w_j中有的个体在w_i中都要有，此即BF为真的条件，可以精确表述为:

满足这一条件的框架有收缩的个体域。相反，BFc为真的条件是，在w_i中有的个体在w_j都要有，可以精确表示为:(www.xing528.com)

满足这一条件的框架有扩张的个体域。如果一个个体域既是收缩的又是扩张的，则称它为等同的个体域。前面所述的必然等同系统和必然不等同系统都要求等同的个体域，其区别要由模型上的赋值来刻画。故有人说:“BF和BFc表示的是框架的性质，而等词则是赋值的性质，或模型的性质。” ⁽¹⁰⁾

蒯因论证说，de re模态必然导致本质主义。以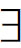（x）□F（x）和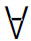（x）□F（x）为例。前者说，存在这样的x，它必然地是F，或者说，它必然地具有属性F；后者说，对任意x而言，它必然地是F。这就承认了事物的有些特征是其必然具有的，有些则是其偶然具有的。亚里士多德认为，本质特征是（1）某些对象具有而其他对象不具有的，（2）具有它们的对象就必然地具有的特性。于是，蒯因作出结论说，容许有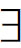（x）□F（x）这类语句的模态逻辑显然是“回到亚里士多德的本质主义”，“拥护量化模态逻辑的人必然赞成本质主义” ⁽¹¹⁾。蒯因是反对本质主义的，他认为这种哲学是“不合理的”，因为本质主义讲本质属性，归根结底要跑到承认共相的实在论或柏拉图主义那里去。

de re模态的另一个后果就是导致承认跨越世界的个体，由此又引出所谓的“跨越世界的同一性”和“跨越世界的辨认或识别”问题。应该指出，这不是两个问题，而是同一个问题的两种不同说法，最后与本质和本质主义有关。这留待第六节去讨论。