指称晦暗性：同一替换与存在概括

二、指称的晦暗性:同一替换和存在概括

蒯因证明，模态词造成晦暗语境，它使同一替换规则和存在概括规则失效。

在经典谓词演算中，有所谓的同一性原理:如果x和y等同，则x具有什么性质y就具有什么性质，其形式表述是:

这一原理在模态语境中，相应地在模态逻辑中却不成立。请看下面的例子:

（1）9必然大于7。

（2）必然地，如果在暮星上有生命，那么在暮星上有生命。

这里，（1）是数学真理，（2）是逻辑真理，它们都是真命题。

但是，下述命题则应被看成是假的:

（3）行星的数目必然大于7。

（4）必然地，如果在暮星上有生命，则在晨星上也有生命。

这是因为，行星的数目大于7，暮星＝晨星，都只是偶然的经验事实，而不是必然的。

下述两个命题则是被天文学证实了的真理:

（5）行星的数目＝9。 ⁽³⁾

（6）暮星＝晨星。

但我们根据（5）、（6），使用同一替换规则分别对（1）、（2）进行替换，结果得到（3）、（4），即通过同一替换从真命题得到了假命题。蒯因分析其原因时指出:“重要的事情是要了解‘必然地……’和‘可能地……’这两个语组，像引文和‘不知道……’、‘相信……’一样，是在指称上暧昧的。” ⁽⁴⁾这就是说，模态词的出现使得单称词项在指称上暧昧，从而使得同一替换规则无效。

蒯因还进一步考虑了在模态语境中使用量词的情况。在经典谓词逻辑中，有一条下述形式的存在概括规则:

F（y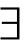）→（x）F（x）

其意思是，如果某一个体y是F，则至少存在一个个体x是F。例如从“2是偶素数”，可以得到“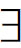（x）（x是偶素数）”。蒯因证明，当把这一原则应用于模态语境时，它也不再普遍成立。例如，从前面的例（1）实施存在概括，就可得到:

（7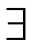）（x）（x必然大于7）(www.xing528.com)

从例（2）实施存在概括，可以得到:

（8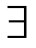）（x）□（如果在暮星上有生命，则在x上有生命）

按照蒯因的观点，存在就是成为约束变元的值。于是，（7）和（8）分别承诺了一个个体存在。（7）说，存在一个必然大于7的个体；（8）说，存在一个个体，使得“如果在暮星上有生命，则在x上有生命”是必然的。那么，（7）和（8）分别承诺的个体究竟是什么呢？先看（7），（7）是从（1）推出的，因此“必然大于7”的个体当然是9，但是指称9这同一个体却有两种方式:一是自然数9，一是行星的数目。若把自然数9用作（7）中约束变元的值，则得到真语句“9必然大于7”；若把“行星的数目”作为（7）中约束变元的值，则得到假语句“行星的数目必然大于7”。于是，（7）和（8）的真值就不是唯一的，它们依赖于约束变元x所代表的个体的指称方式:在某一或某些指称方式之下，它们是真命题；在另一或另外一些指称方式之下，它们则是假命题。而对于x所代表的个体有不同的指称方式，这并不是个别现象，因此总有这样一种可能:从真命题出发，通过应用存在概括规则，得到一个假命题，即存在概括规则失效。

蒯因还谈到了全称示例原则。这一原则的形式是:

（x）F（x）→F（y）

其意思是:如果（论域中的）一切个体都是F，则（论域中的）某一个体是F。蒯因指出:这一原则与存在概括是同一个原理的两个方面。既然已经证明存在概括规则在模态语境中不成立，全称示例原则在模态语境中当然也不成立。

由此，蒯因得出一般性结论:“如果我们把量词应用于某变元的一个指称暧昧的语组，并想要它从该指称暧昧的语组之外约束那个变元，那么我们最终得到的就是……无意义的话或者是不具有我们想要的涵义的话。一句话，我们一般都不能正当地对指称暧昧的语组进行量化。” ⁽⁵⁾

我认为，同一替换规则和存在概括规则之所以在模态语境中失效，其原因至少有两个:（i）在一阶逻辑中，实际上只考虑词项在单个世界（例如现实世界）中的外延；在模态逻辑中，由于模态词的引入，需要考虑词项在所有可能世界中的外延。由词项在现实世界中外延同一，并不能确保它们在所有可能世界中都外延同一。例如，“暮星＝晨星”在现实世界中为真，但不能保证该语句在所有可能世界中都真，于是，从“必然地，如果在暮星上有生命，那么在暮星上有生命”，就不能通过同一替换推出“必然地，如果在暮星上有生命，那么在晨星上有生命”。（ii）词项之所以在不同的可能世界中会有不同的外延，是因为按通常的观点，词项既有外延又有内涵，并且是内涵决定外延，即是说，词项的内涵是识别、确定词项的外延的根据和标准；但由于各个可能世界有所不同，其中的个体也有所不同，同样的内涵在不同的可能世界中就有可能识别出不同的外延，或者说同样的外延在不同的可能世界中有不同的识别标准即内涵。

基于上述认识，不同的模态逻辑学家采取了下述不同的技术解决方案，其中之一是将同一强化为必然同一，即所有可能世界中的同一。有一类模态谓词逻辑系统包含这样的定理:

其意思是:如果x和y等同，则它们必然等同。这样的系统叫做必然等同系统。顺便说一下，也有必然不等同的系统，即其中有这样的定理:

其意思是:如果x和y不等同，则它们必然不等同。

使同一成为必然同一的具体做法有:（i）克里普克的严格指示词理论:专名没有涵义，只有所指，是纯指称性的，它们在所有可能世界中指称同一个个体，故叫做严格指示词；而摹状词包含关于对象性状的描述，有涵义，因而在不同的可能世界中有可能指称不同的对象，是非严格指示词。在模态语境中，不能用非严格指示词去代入、替换严格指示词，否则会由真命题得到假命题。（ii）大卫·刘易斯的限界个体（bound－world individual）理论:个体不能跨越不同的可能世界而存在，只能存在于一个可能世界中，是受制于世界的。这样一来，如果两个体在某个可能世界中同一，则述说它们同一的命题在任何可能世界中都不会是假的，因为它们在其他的可能世界中根本不出现；于是，它们之间的同一也就（空洞地）成为必然同一。（iii）令所有可能世界都有相同的个体集。用H（w_i）表示可能世界w_i中所有个体的集合，用D表示所有可能世界中所有个体的集合，（iii）所要求的实际上是H（w_i）＝D。再用t表示一个模态系统中的任一词项，V（t，w_i）表示t在可能世界w_i上的赋值，则使（□＝）有效的赋值必须满足下述条件:

对于任意的w_i，w_j∈W，若R（w_i，w_j），则V（t，w_i）＝V（t，w_j）。

而使（□≠）有效的赋值则必须满足下述条件:

对于任意的w_i，w_j∈W，若R（w_i，w_j），且V（t，w_i）≠V（t′，w_i），则V（t，w_j）≠V（t′，w_j）。

显然，在满足上述两个条件的模型中，任意两个世界的个体集必定相同。

必然等同系统排除了偶然同一，而在现实世界中偶然同一是大量存在的，如暮星＝晨星，北京＝中华人民共和国首都。于是，有的逻辑学家如亨迪卡通过限制同一替换规则在模态语境中的使用，构造了偶然等同的系统，其中的赋值满足这样两个条件:

以上说明，同一替换规则和存在概括规则在模态语境中的失效，对于模态逻辑来说并不像蒯因所说的那样是致命的，在哲学上对此完全可以有合理的说明，在技术上也有完全合适的办法去处理它们，并且由于哲学思想或理论出发点的不同，还可以有不同的技术处理方案。