形式化方法在当代中国人文探索中的作用与限度

四、形式化方法的作用和限度

1.形式化的必要性

第一，形式化为科学研究提供了一种新的视角和新的思考方式。

可以说，把语言、定理、理论区分为不同层次，并要求在较高的层次（n＋1）上去讨论、叙说或断定较低层次（n层）的一般性质，这是形式化研究的一个极其重要的成果。这一成果的方法论意义就在于，要求我们大力开展元理论研究，这里的“元”（meta－）是指“在……之后”、“次一层的”或“超越”的意思。元研究就是以某一理论自身作为研究对象的次一层的研究，关于对象理论的各种研究及其结果构成元理论，还可以对元理论本身进行研究，构成元元理论……这种元研究与对象理论内部的研究相比，意义更为重大，因为后者只是在对象理论之内解难题、补漏洞，以使对象理论更趋成熟和完善，它并不对对象理论本身、对这些难题本身的价值提出怀疑，这就很难导致对象理论研究在根本性前提上实现重大层次跃迁。而元研究则把锋芒对准对象理论本身，它使我们能在更广阔的视野中，重新审查对象理论的对象、性质、根基及其正当性、有效性等，从而使我们能够不断地调整或修正对象理论的研究，使对象理论研究减少盲目性，以便更为成功和有效。因此，由形式化派生出的这种元研究方式就为一切其他科学，包括自然科学和哲学社会科学，提供了一种新的视野和新的研究方式。其他科学领域已经明显受到了这种研究方式的影响，如数学领域有元数学。而在哲学领域内元研究也方兴未艾，例如有元哲学、元伦理学、元美学等，其中元伦理学最为完善，几乎成为当代伦理学研究中最主要的倾向和派别。有人认为，一门学科的重大变革，首先是在元科学层次上的变革，随后才是该门学科中基本问题的转换。“哲学需要元理论” ⁽¹⁷⁾。我同意这种看法。

第二，形式化有助于提高一个理论的严格性和精确性，有助于排除理论思维中的谬误。

非形式化理论常常是用自然语言或者再加上某种特定的符号语言表述的，而自然语言本身具有一系列严重的缺陷，例如不精确，语义模糊，充满歧义，语法关系很不严格，这就使得用它表述的概念和命题很可能被误解和误用；并且，用自然语言表达的推理常常是结合内容和意义的，在形式上不那么严格，有可能发生这样的情况:在推理过程中暗中假定或使用了另外一些其正确性有待证实的前提或规则，而后者往往成为思维谬误的一个源泉。上述现象在形式化系统中是不可能出现的，这是因为:（1）形式系统的语言排除了任何模糊性和歧义性。形式系统一开始就陈述它的字母（初始符号），这种字母是特制的符号语言，除了用自己的形状表达结构信息外，不再具有任何意义，因而是单义的；并且，它明确规定了例如由字母生成词（项）、由词生成句（公式）的句法规则，这些规则是递归定义的，即明确规定了在一步做了之后下一步如何做。（2）形式系统内的证明或推导是极其严格的，以K的“证明”概念为例:“K中的一个证明是一个合式公式的有穷序列A₁，…，A_n，其中每一A_i（1≤i≤n）或者是一公理，或者是一已证的定理，或者是由先前的公式经使用变形规则得到。”因此，这就排除了使用任何隐含前提或未明确陈述的规则的可能性。（3）形式系统一般能在有穷步内判定:一个符号是否为初始符号，一个符号序列是否为公式，一个公式是否为公理，一个公式是否能从给定公式利用变形规则得到，一个有穷长的公式序列是否为一证明。即使形式系统使用了非初始符号、非公式、非公理、非系统的变形规则，利用判定程序也很容易查明并立即排除。因此，模糊和歧义（不精确），使用暗含的前提和未明确陈述的规则（不严格）的错误，在形式系统中是不会出现的，在精确性和严格性方面形式系统堪称典范，把一个成熟的科学理论表述为这样的形式系统，当然是极有好处的。

这里以中国某一时期的哲学研究为例，可以看出在精确性和严格性方面确实存在的许多弊端。例如，搞哲学的几乎谁都知道，列宁曾把概念、范畴比作人们认识和掌握自然现象之网的网上纽结，它区分着人类认识世界的过程中的一些小阶段。但是天知道人们有时赋予同一个“网上纽结”以多少或多么不同的意义，这只要反思一下改革开放初期关于“真理有无阶级性”的大讨论就够了。有人说，真理是客观的，没有阶级性；有人说，自然科学的真理没有阶级性，而社会科学的真理有阶级性；还有人说，真理本身包含有谬误的内容；更有这样的推理:“马克思主义是有阶级性的，而马克思主义是真理，所以有些真理是有阶级性的。”仔细分析一下就会发现，人们是在多少和多么不同的意义上使用“真理”、“阶级性”等概念。再如，辩证唯物主义有一条最基本的原理:事物都是普遍联系的，严格的分析表明，这一命题是有歧义的，它至少容许以下六种强弱不同的解释:（1）所有的事物与所有的事物相联系；（2）所有的事物与有些事物相联系；（3）所有事物与某个事物相联系；（4）有些事物与所有事物相联系；（5）有些事物与有些事物相联系；（6）某个事物与某个事物相联系。“事物都是普遍联系的”这一原理究竟说的是哪一种意义？还有，时下的许多哲学论著几乎有一个通病:缺乏论证性，其中充满了新名词、新概念、新材料，云山雾罩，而遇到一些十分关键的思想，却轻描淡写，几笔带过，并且时常可见内容混杂、重叠，甚至冲突之处。无论怎样辩解，上述弊端绝不是一个好的哲学理论所应当具有的。马里奥·邦格曾指出:自19世纪以来，唯物主义没有取得进步，“这部分地是由于它无视现代逻辑并拒绝向对立的哲学学习”。“大多数唯物主义哲学家都只说日常语言，从而必然只能以一种不精确的方式来表达自己的观点——他们很少考虑以一种令人信服的方法对自己的观点进行论证。”他认为:“哲学研究应当系统地、精确地和科学地进行，而不能采用文学的描述方式。” ⁽¹⁸⁾我认为，马里奥·邦格的意见是值得重视的。哲学的本性在于爱智慧，它是说理的，理所当然地应当加强论证性，使其逐步精确化、严格化。应该认识到，精确化、严格化不仅仅是组织观点与材料的写作方式问题，而是把哲学思考引向深刻化、正确化的途径与方法。这是因为:（1）严格化、精确化必须以哲学思考的周密化、细致化为前提，而周密、细致思考的结果往往导致哲学思想的全面与深刻；（2）有些哲学理论泛泛而论可能十分动听、十分在理，但是一旦要使其严格化、精确化，要与其他观点处于有机统一之中，往往就会发现它漏洞百出，有些甚至根本不能成立，纠正错误则导致哲学思考的正确化。形式化作为现代逻辑最重要的方法，完全有必要应用于哲学研究，以促使后者走向精确化和严格化。

第三，形式化有助于揭示一个理论的概念、范畴、命题的潜在涵义及其相互之间的潜在逻辑关系，从而促使理论研究走向深入。

例如，在非形式化理论中，通常也要分析相关概念、范畴的潜在逻辑涵义，也要进行推理，理清相应命题之间的逻辑关系，以把这些概念、范畴、命题构成有机的理论体系。但是，这种分析和推理的链条常常是很短的，最多也就是三四个层次或三四步。而在形式化系统中，推理的链条在原则上可以无限延伸，因而可以得出无数条新定理，这就可能造成下述结果:原先没有意识到或模糊地意识到的涵义和逻辑关系现在被明确地、充分地揭示出来了；原先以为没有逻辑关系的，现在被证明是有关系的；或者，原先认为逻辑上一致、相容的，现在可能揭示出其潜在的逻辑矛盾，如此等等。这样一来，科学研究无疑就被大大向前推进了。例如，义务、允许、禁止、承诺、应该等概念是伦理学所要研究的，新兴的道义逻辑就是以包含这些概念的语句的逻辑特性和推理关系为对象的，它导出了许许多多有关这些概念的新定理，这些定理有助于把模糊的伦理学概念精确地加以规定，并且把它们潜在的涵义和关系阐发清楚。并且，道义逻辑还触及到一些深刻的伦理学问题，例如义务、允许、禁止与必然、可能、不可能的关系，义务的相对性和条件性，义务和伦理规则的关系，伦理规则集的层次性，义务的冲突与矛盾及其克服，等等。所以，道义逻辑一方面为伦理学研究提供了工具，另一方面又深化了伦理学研究。

第四，形式化有助于不同观点的比较和辨识，为不同观点之间的交流、讨论、批判提供了前提和基础。

当一种观点以一种大而统之、简而化之的方式提出时，几乎不能与其他观点比较，因为它不具有确定的形式，弹性较大，就像一条满身黏液的泥鳅把捉不住。但一旦利用形式化方法使其精确化和严格化之后，就可以进行相互比较和相互批判，弄清楚它们之间的真实关系。例如，哲学家们对于时间有各种各样的看法和观点。例如，认为时间是有始有终的，或有始无终的，或无始有终的，或无始无终的，又认为时间是不可分的或无限可分的，连续的或离散的，还认为时间是一维决定的，或多维非决定的，等等。作为哲学逻辑一支的现代时态逻辑，就从上述各种不同的哲学观点出发，构造了各种不同的时态逻辑，例如线性时态逻辑，枝形时态逻辑，无端点线性（或者枝形）时态逻辑，稠密无端点线性（或者枝形）时态逻辑，离散无端点线性（或者枝形）时态逻辑，这些不同的时态逻辑分别刻画着不同的时间观，但由于这些逻辑是严格构造的形式系统，因而它们之间的关系是十分清楚的，而这在直观、朴素的观点中是根本做不到的。

2.内在的局限

形式化并不是普遍的和万能的研究方法，相反，它是具有很大局限性的，具体表现在:

第一，适用范围的狭窄性。这主要是指:（1）并不是一切理论都能够被形式化。前已指出，只有那些发展得比较成熟、逻辑关系比较清晰的理论才可能形式化，而那些发展得很不成熟、逻辑关系十分混乱的理论是没法形式化的。正因如此，我才反复强调，在把一理论形式化之前，先要进行一番预备性研究工作，考察其中概念、命题的精确涵义，理清它们之间的逻辑关系。若是比较成熟的理论，这种预备性研究所花气力就会较小，并较容易取得成功。相反，若一个理论很不成熟，那么首要的任务就不是形式化，而是对它所面临的难题和困境本身进行研究，促使其成熟。并且，只有那些自足的理论，即那些围绕一特定的主题，逻辑上层层展开，自我表达、自我论证的理论才适于形式化，而那些以论战性为主的论著是不适于形式化的。（2）并不是一个理论的一切方面都能够形式化。形式化只适于考察一个理论中概念或命题的形式方面和以严格意义上的逻辑方面为内容的那些问题，具体来说，它只能在下述三点上起作用:（i）更严格、更精确地限定概念、命题的涵义，（ii）更清晰地展示概念、命题之间的逻辑关系，（iii）尽可能多地展开它们的逻辑推论，以揭示概念、命题的潜在逻辑涵义。形式化对除此之外的其他方面是无能为力的。以哲学理论为例，形式化并不过问:究竟是物质第一性，还是精神第一性？整个世界是联系和发展的，还是孤立和静止的？等等。但形式化处理这样的问题:如果物质是第一性的，我们能够由此推出什么？这一命题的逻辑后承有哪些？很明显，形式化的适用范围是比较狭窄的。

第二，研究结果的尝试性。这是指，应用形式化方法所得到的形式理论，只是一种暂时性和尝试性的理论。雷谢尔指出:“这是毫无疑义的，科学理论从来不具有最终的和绝对的确定性，总是受到新的事实材料的反驳或修正；科学理论总是由新的和反驳性的观察所左右。同样，运用形式化方法所建立的任何系统，如果与新发现的事实不相符合，即导致了迄今为止未预见到而直观上又是不可接受的结果，就会被推翻。的确，无论这种理论同我们对所研究领域的非形式理解多么一致，不一致的可能性永远不会完全被排除。我们的逻辑的和概念的预见力从来不会如此敏锐，以致概念的系统化理论可能导致不可接受的结果，这样一种偶然性会从可能性的领域中消失。” ⁽¹⁹⁾马里奥·邦格也指出，形式化确实使哲学理论增加了严格性和精确性，但精确性并不能保证正确性，而是使我们易于发现错误并改正它；精确性也不能保证深度和重要性，而是使我们有可能对哲学理论进行合理的检查，以诊断问题和困难的确切来源，同时也为它们的解决提供方法。 ⁽²⁰⁾在我看来，形式理论的尝试性有两个来源:（1）依据形式化方法，每一具体的研究都依赖于对非形式系统进行形式系统化，然而，在关于任何对象的非形式思想中，在相关性、一致性和清晰性方面总存在着某种程度的松散性或薄弱性，甚至其基本命题、基本观点本身就是错误的。作为出发点的这种松散性或可能的错误必然要反映为作为结果的系统化理论的暂时性。（2）在构造形式系统时，在形式语言和演绎装置的设计与选择上存在问题。具体来说，形式系统所选择的初始概念和公理可能不是被形式化理论中最基本的概念或命题，或者其涵义不同于它们的原型在被形式化理论中的涵义，或者形式系统的推理规则选择不当，其中有些规则的推演能力太强或过弱。这就可能造成下述结果:被形式化理论中的许多概念和命题，在相应的形式理论中并未被派生或推导出来；形式化理论的概念、命题严重偏离被形式化理论，以至于前者和后者不相干，即不能把前者看成对后者的适当形式化；在形式理论中出现了被形式化理论中不存在的悖论性结果，如此等等。因此，形式化理论也是一种尝试性理论，其中的命题和定理是可错的。

第三，作用程度的有限性。这是指，形式化方法并不是法力无边的，它对于某些问题是无能为力的。具体来说，对于足够复杂的形式系统S而言，（1）如果S是逻辑上无矛盾的，则S必然是不完全的，即并非所有的真命题都在S中可证；（2）必然是不可判定的，即不存在可以用来判定其中的任一命题是否可证的算法；（3）它的真概念在本系统中是不可定义的。哥德尔不完全性定理，丘奇—图灵的不可判定性定理和塔斯基的真概念不可定义性定理，分别表达了形式系统上述三个方面的局限性。哥德尔于1931年证明:（1）一个形式系统S如果包括形式算术系统作为子系统，它就是不完全的，即存在一个语句A，A和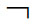A在S中都不可证。这被称为第一不完全性定理，它有一个系理，即（2）如果这样的系统是一致的，那么其一致性在本系统内不可证。这被称为第二不完全性定理。上面提到的形式算术系统是指自然数算术理论的形式化，它是由带等词的一阶逻辑系统再加上表示自然数算术所必要的初始符号、公理、规则之后所得到的形式系统。最近有人证明，在作为哲学逻辑一支的模态逻辑中，存在着无穷多个不完全的正规模态系统。丘奇于1936年证明:如果形式算术系统是一致的，那么它就是不可判定的，即没有一个机械的程序去判定任一合式公式是否可证。显然，既然形式算术系统就是不可判定的，那么，任何包含形式算术系统作为子系统的系统也是不可判定的。作为这一定理的系理，丘奇还证明:一阶逻辑也是不可判定的。图灵于1937年也证明了这一结果。塔斯基于1933年证明:在像形式算术系统这样丰富的系统中，我们不能定义这一系统内命题的真假等语义学概念。既然在形式算术系统中都不能定义该系统的真概念，任何包含形式算术系统作为子系统的形式系统更是无法在自身中定义本系统的真命题。这三大定理以严格的数学证明的形式，充分揭示了由形式化方法得到的形式系统的局限性，因此被称为局限性定理。

以上说明，形式化只是科学研究的一种重要的辅助性方法，必须注意把它与其他研究方法配合使用，共同为我们的研究工作服务。相反，如果夸大形式化的作用，把它看作是一种普遍的、万能的研究方法，用它去取代其他的科学研究方法，则是错误的。因此，下述的告诫是值得认真注意的:“当前也要注意一种潜伏的暗流。对哲学的种种领域存在作成功的逻辑分析的可能性，可能吸引人们把对具有本质意义的重要问题的注意，转向安逸地寻求某些细枝末节的小问题。他们可能放弃对某些尚未梳理清楚的哲学领域作艰苦卓绝的探索，而对某些本质上是平凡的问题做过分精湛的逻辑分析。” ⁽²¹⁾

【注释】

(1)波亨斯基:《当代思维方法》，邵春林等译，44页，上海，上海人民出版社，1987。

(2)见马蒂尼奇编:《语言哲学》，599页。(www.xing528.com)

(3)罗素:《数理哲学导论》，159～160页。着重号系引者所加。

(4)参见Hintikka，J.Lingua Universalis vs.CalculusR atiocinator:An Ultimate Presupposition of Twentieth－Century Philosophy，Kluwer Academic Publishers，1997，pp.viv－xxii，104－139；‘On G9del’s Philosophical Assumptions’，Syntheses 114（1）:13－23，1998。

(5)张家龙:《数理逻辑发展史——从莱布尼茨到哥德尔》，294页，北京，社科文献出版社，1993。

(6)Frege，G.Philosophical and Mathematical Correspondence，Oxford:Blackwell，1980，pp.37，43.

(7)参看本书第十二章第一节有关蒯因思想的评述。

(8)参见Hintikka，J.‘On G9del’s Philosophical Assumptions’，Syntheses 114（1）:13－23，1998。

(9)参见徐利治:《数学方法论选讲》，55页，武汉，华中工学院出版社，1983。

(10)转引自瑞德:《希尔伯特》，袁向东等译，72页，上海，上海科技出版社，1982。

(11)在阅读本小节以下内容之前，请先参看下一章第一节。

(12)Hilbert，D.‘On the infinite’，in Philosophy of Mathematics:Selected Readings，ed.by P.Benacerraf and H.Putnam，Prentice－Hall，Inc.，1964，p.151.

(13)Hilbert，D.and P.Bernays:Grundlagen der Mathematik，vol.1，Berlin，1934，p.32.

(14)中国社会科学院哲学研究所逻辑研究室编:《数理哲学译文集》，62页，北京，商务印书馆，1988。

(15)中国社会科学院哲学研究所逻辑研究室编:《数理哲学译文集》，132页。

(16)转引自夏基松、郑毓信:《西方数学哲学》，109页，北京，人民出版社，1986。

(17)李光程:《哲学究竟是什么？》，载《哲学研究》，1987（12）。

(18)马里奥·邦格:《科学的唯物主义》，张相轮、郑毓信译，4～5、22～31页，上海，上海人民出版社，1989。

(19)Rescher，N.Topics in Philosophical Logic，Dordrecht:Reidel，1968，pp.332－341.

(20)参见马里奥·邦格:《科学的唯物主义》，4页。

(21)朱水林:《现代逻辑引论》，9页，上海，上海人民出版社，1989。