希尔伯特规划与形式主义：当代中国人文大系

三、希尔伯特规划和形式主义

1.希尔伯特规划

所谓“希尔伯特规划”，是由著名德国数学家希尔伯特于20世纪初期提出的一种数学方案，其要点是:将各门数学形式化，构成形式系统或形式理论，然后用有穷方法证明各形式系统的一致性，从而导出全部数学的一致性，以此保卫古典数学。

19世纪末和20世纪初，随着罗素悖论等一系列逻辑—数学悖论的发现，引发了第三次数学危机。在危机面前，不同的逻辑学家和数学家们采取了不同的态度。例如，策梅罗建立了公理化集合论，罗素提出了逻辑类型论，布劳维尔等直觉主义者则从其直觉主义数学观出发重建数学。各种方案都存在这样或那样的问题，其中尤以直觉主义为甚。直觉主义者把数学基础危机归罪于引进“实无穷”和在无穷集合中使用“排中律”，因而极力排斥承认“实无穷”的康托尔集合论和“排中律”在古典数学中的应用，否定在古典数学中的大量非构造性定义和纯存在性证明，从而摈弃大部分古典数学成果。希尔伯特不同意直觉主义者的做法，这源自于他在“实无穷”问题上与直觉主义者有原则性分歧，但他与后者也有某种类似之处。所谓希尔伯特规划的提出，最终要归结为他对实无穷所持的这种矛盾态度。

一方面，希尔伯特认为，实无穷是数学思维中不可缺少的，数学的各个分支都包含无穷集合，数学分析在一定意义上是一部“无穷的交响乐”。因此他认为，涉及实无穷的古典数学是“我们最有价值的宝藏”；康托尔集合论作为关于实无穷的理论，是数学精神最值得惊叹的花朵，是人类理智活动的一个最高成就；排中律是一个普遍适用的逻辑原则，在数学中禁止使用排中律就像在天文学中禁止使用望远镜一样荒谬。但另一方面，他又对实无穷持有种种保留和疑虑。他认为，绝对无穷概念“确实是超越人们的直观性证据之外的”的东西，它们是“通过思维过程而被嵌入或者外推出来的”东西，“在实在中无处能找到无穷。它既不存在于自然中，也没有为理性思维提供合法的基础” ⁽¹²⁾。因此他认为，绝对的可靠性只存在于有穷的范畴内，对实无穷的任何指涉都是不那么可靠的。但鉴于无穷概念在数学理论中的特殊重要性，以及它所带来的简明性和方便性，我们仍然有必要把实无穷作为理想元素引入到数学中来。于是，希尔伯特把全部数学分为两部分:只包含有穷成分的“现实数学”和涉及实无穷的“理想数学”（大部分古典数学正是这样的理想数学）。他认为，尽管理想数学不具有真实的意义，但只要能证明这种理论不会导致错误，特别是不会导致悖论，那么这些数学仍是可靠的，仍应当在数学科学中保留它们的地位。

希尔伯特还把数学分为三类:（1）非形式化的数学，即通常的直观的数学；（2）形式化的数学，即把通常的数学表示为形式系统的结果；（3）元数学，亦称证明论，它是以形式化数学为研究对象的一种数学，其主要目的是证明各个数学分支的绝对一致性。希尔伯特规划就是要把非形式化的数学表示为形式化数学，然后证明各形式化数学系统的绝对一致性，并且在证明中只能使用有穷程序或有穷方法。关于有穷方法，希尔伯特和贝尔奈斯解释说:“我们总是用‘有穷’一词来表示，所说的讨论、断定或定义限制于其对象可以彻底生成并且其程序可以彻底实行，因此是在具体观察的范围内进行的。” ⁽¹³⁾具体来说，有穷方法有以下要点:（1）每一步只考虑确定的有穷数量的对象，承认潜无穷，但不处理实无穷对象；（2）论域、判断或定义的对象必须满足能彻底给出，其过程能彻底进行；（3）全称命题只能在假言意义下理解，即任给一个对象都能有穷地证实它具有所说的性质；（4）存在命题则理解为确实能给出具有所说性质的对象，或者有一个能确定这样一个对象的有穷程序；（5）对于遍历无穷论域的量化命题，排中律不成立，因为可以有这样的情形:既不能有穷地证明一个量化命题是真的，又不能有穷地证明其否定命题是真的；（6）数学归纳法作为证明的一个有穷方法是允许的，因为若用归纳法来证明“对于所有的n，P（n）”这一命题，那么它表示我们也只用到从0到n个数来论证对于任给的一个n，n都有P性质。这就是说，归纳并不要求引进自然数的古典的实无穷。由此可以看出，有穷方法实际上就是一种能行方法，即在有穷步内凭借一个机械的程序可以完成，并得到唯一确定的结果的方法。

希尔伯特规划要通过以下三步来实现:（1）把所要讨论的古典数学理论T（如初等数论、集合论和数学分析彻底）形式化，加上逻辑演算，构成一形式系统TF，原数学理论中的基本概念被转换为形式系统中的初始概念，命题转换为符号公式，推演规则转换为符号公式之间的变形关系，证明转换为符号公式的有穷序列；并且在这样的系统中，下述各点必须能行可判定:一符号是否为初始符号；一符号序列是否为合式公式；一公式是否为一公理；一公式是否能根据变形规则从先前公式得到。（2）从不假定实无穷的有穷观点出发，建立一个元理论TM作为研究上述形式系统的工具，TM包括一个逻辑系统和初等数论。这样建立的TM被称为“元数学”（证明论）或“有穷逻辑”。（3）用元数学TM去证明:在形式理论TF中不会产生矛盾，即不会在其中同时推出某个论断A与其否定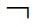A，也就是证明形式理论TF的一致性。如果能够证明TF的一致性，则TF所摹写的古典数学理论T及其理想命题也不会产生矛盾，都可以保留。

希尔伯特规划提出后，曾受到广泛关注，产生了很大影响，并得到了一些局部性结果。但哥德尔在试图按希尔伯特规划行事的过程中，却得到了一个否定性的结果:如果一个包括初等数论的形式系统是一致的，那么其一致性不能用有穷方法甚至不能用一阶逻辑和初等数论的方法来证明。这就是著名的哥德尔第二不完全性定理，它给希尔伯特规划以沉重打击。它表明:对元理论的有穷主义要求应当放宽，应允许使用比有穷方法更强的超穷方法。后来确实有人用超穷方法证明了初等数论的一致性，但这已经不是希尔伯特原来的设想了。希尔伯特规划尽管按其本意是失败了，但却从中产生了许多积极的成果，其中最直接的结果是证明论作为数学和逻辑的重要分支之一得以形成和发展。(www.xing528.com)

2.形式主义

“形式主义”是20世纪上半叶在关于数学基础的论战中所出现的一种数学哲学思潮，可以把它看作是极端唯名论观念在数学中的表现。自称形式主义者的有柯里、鲁宾逊和柯恩等人。鲁宾逊在《形式主义64年》一文中说道:“我对数学基础的看法，主要根据以下两点，或者说两条原则:（i）不论从无穷总体的哪种意义来说，无穷总体是不存在的（即不管是实在的还是理想的无穷总体都是不存在的）。更确切地说，任何讲到或意思上含有无穷总体的说法都是没有意义的。（ii）虽然如此，我们还是应该‘照常’继续搞数学这个行业，也就是说，应该把无穷总体当作真正存在的那样来行事。” ⁽¹⁴⁾概括起来说，形式主义者不承认数学对象的客观实在性，把数学等同于纯粹意义的符号操作，认为数学对象的存在性和数学命题的真理性就在于它们的一致性，“数学的存在即无矛盾”。

形式主义者不赞成关于数学对象的实在论或柏拉图主义的观点，在后两者看来，数学对象是独立于思维而存在的，对此人们只能去认识，而不能任意创造或改变。而在形式主义者看来，实在论至少有两大致命伤:一是它肯定实无穷没有直观上可信的合理根据。例如柯恩指出:“我相信任何实在论者都会承认的一个弱点，是他没有能力说明像更高的无穷公理这类更高的公理的无穷无尽序列的根源。当考虑一个充分不可达的基数时，甚至最坚定的实在论者也一定会退缩的。还存在像可测基数公理这样的公理，它们比曾经考虑过的最一般的无穷公理还要强，但是看来绝对没有直观上可信的证据，以便拒绝还是接受它们。近年来的独立性结果是对实在论立场的另一个挑战。关于这最后一点，有些人觉得某些直观上可接受的公理最终会解决连续统和其他类似的问题。另一方面，可测基数公理，甚至不支持这样一种解决的最模糊的前景，却好像命定地要被热心的集合论理论家作为一个公理来采用。” ⁽¹⁵⁾二是它构成对数学研究中自由思想的压制，因为它认为我们只能认识而不能创造数学对象。在形式主义者看来，数学对象在现实世界中是不存在的，只是数学家思维的自由创造，是一种“有用的虚构”。

形式主义者认为，数学是研究推理或形式推理的，即从一定的形式前提（公理），按照演绎推理的规则，把一定的语句作为数学定理推导出来。数学是一门关于形式系统的科学，它所研究的只是一些事先毫无意义的符号系统，数学家的任务只是为某一符号系统确定作为前提的合式的符号串，并给出确定符号之间形式关系的变形规则，从前提按给定的变形规则得出作为定理的符号串。因此，数学就是符号的游戏，从事数学研究如同下棋，所驱遣的数学对象就像无实在意义的棋子，按给定的变形规则对符号进行机械的变形组合，就像按下棋规则去驱动棋子。对这种游戏的唯一要求就是它的无矛盾性（柯恩），此外也许还要考虑到“是否方便，是否富于成果”（柯里），以及结构上是否美（鲁宾逊）等。

毫无疑问，形式主义的许多思想可以在希尔伯特那里找到渊源，前者是把后者的某些思想极端化的结果。因此，希尔伯特本人很多时候也被看作是形式主义者，但真实情形并非如此。希尔伯特提出以他的名字命名的证明论方案，倡导形式公理化研究方法，主张构造抽象的形式系统，但他并不认为数学只是一套没有现实意义的符号操作，也不否认数学对象的客观实在性，他把数学分为处理不涉及实无穷的现实数学和涉及实无穷的理想数学两部分，尽管他对实无穷的存在性抱有疑虑，但并不完全否定它的存在，相反认为实无穷是数学思维中所不可缺少的，因此把它作为理想元素引入数学，他本人于是被称为“方法论上的实无穷论者”。在他看来，不涉及实无穷的那部分数学却是“现实的（real）数学”，其可靠性和真理性是毋庸置疑的。至少在这一点上，他严格区别于形式主义者。

形式主义对关于数学的形式化研究的重要性及其意义的强调无疑是有价值的，但它的两个核心观点却必须受到挑战:一是由否认实无穷的实在性进而否认所有数学对象的实在性。数学对象是否存在？回答这个问题时首先要弄清楚“存在”一词的意义，像自然数、无穷集这样的数学对象肯定不是像太阳、某头北极熊这样的个体事物在这个世界中那样“存在”着，数学对象的“存在”有另外的意义。我将在后面的“逻辑中的本体论承诺”一章中对此作出解答。二是把数学对象的存在性和数学命题的真理性完全归结为“一致性”或“相容性”。对此西方数学哲学家们早就提出了尖锐的批评。例如直觉主义的代表人物布劳维尔指出:“形式主义数学借助于其无矛盾性证明而获得的逻辑证实包含了一种恶性循环，因为这种证实事实上已经假定了这样一个命题的逻辑有效性，即认为由命题的无矛盾性可以推出它的正确性。”但事实上，理论的无矛盾性并不足以保证其真理性，因为“一个假的理论终究是假的，即使人们找不到矛盾；正如一个犯罪行为总归是罪恶的，不管它有无受到法庭的判决一样” ⁽¹⁶⁾。布劳维尔的上述批评是我所赞同的。