模型:现实世界到可能世界的转变

二、模型:从现实世界到可能世界

从公理学的角度看，公理系统的发展经历了从实质公理化、概括公理化到抽象的形式系统的演变。从语义学的角度看，公理化、形式化系统的解释经历了从现实世界模型到可能世界模型的演变。现实世界模型亦称单世界假定，它把形式系统内的一切符号和公式都解释为现实世界中的对象以及关于这些对象的命题，认为我们能够在形式系统中适当地谈论其存在的一切都必定存在于现实世界中，经过分析最终都是现实世界中的居民。逻辑真理也是关于这个现实世界的真理，只不过所关注的是这个世界的更为抽象和一般的方面或特性。这种观点在罗素的下述话语中得到了最充分的体现:“动物学既不能承认独脚兽，逻辑也应该同样地不能承认，因为逻辑的特点虽然是更抽象、更普遍，然而逻辑关心实在世界也和动物学一样的真诚。……只有一个世界，这就是‘实在的’世界。” ⁽³⁾逻辑学家应该保持一种健全的实在感。可能世界模型亦称多世界假定，是指形式系统的解释框架除现实世界外，还有多个不同的可能世界，逻辑真理并不只与现实世界相关，而是与所有的可能世界相关，逻辑真就是在所有的可能世界中都真。因此，逻辑真理不是关于现实世界的真理，它对于这个世界无所言说，与关于这个世界的事实真理有本质性区别，或者说属于完全不同的真理类型。伴随着语义思考从现实世界模型到可能世界模型的发展，逻辑研究的重心也经历了从语形学（证明论）到语义学（模型论）的变化。

1.现实世界模型

在考虑形式系统的解释时，只考虑现实世界及其对象，就是所谓的“现实世界模型”。这一模型统摄了从直观公理化、实质公理化、概括公理化直至对抽象的形式系统的早期元逻辑研究。利用现实世界模型去解释公理化、形式化系统的，在古代有亚里士多德、欧氏几何、非欧几何、牛顿力学等，在现代则有弗雷格、罗素、怀特海、维特根斯坦、早期卡尔纳普、蒯因、丘奇，根据亨迪卡的研究，甚至还应包括哥德尔和塔斯基。 ⁽⁴⁾

亚里士多德逻辑和欧氏几何是所谓的“实质公理化”的代表。实质公理化是指按一个公理系统只有一个论域的观点去建立公理系统。“具体地说，实质公理学的论域必须先于公理而具体给定，并且是唯一的，然后引入初始概念以表示该论域中的事物，建立公理以刻画这些事物的根本特点，借助演绎推理来证明该论域中的真理。这种公理学是对经验知识的系统总结，公理一般具有自明性。” ⁽⁵⁾

亚里士多德在《后分析篇》中从理论上探讨了这种公理化方法。他认为，一个演绎科学理论可以视作一个关于某一确定领域的概念和命题的体系，其中全部概念分为基本概念和派生概念，后者是由基本概念运用定义直接或间接加以规定的概念；全部命题分为基本命题和导出命题。基本命题包括公理和公设，它们构成系统内一切证明的出发点。公理必须依据经验或直观而明显为真，它们为一切科学所共有，例如逻辑上的矛盾律和排中律，数学上的等量加减等量其结果仍相等；公设则是某一门科学所接受的第一性原则，毋需证明，但其真实与否要接受推出结果的检验。从公理和公设出发，经使用逻辑规则进行推导，得到导出命题，亦称定理。由基本概念和派生概念、公理、公设、推理规则和定理构成的理论体系就是公理系统。在《前分析篇》中，亚里士多德还试图把他的三段论发展成为一个公理系统。他把三段论区分为三个格，共有19个有效式，其中第一格叫做“完善的格”，第二、第三格叫做“不完善的格”。他运用一套化归程序把后两个格化归、还原为第一格，并进一步把全部有效式都化归、还原为第一格的AAA式和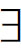A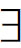式。实际上，把他的这套化归程序倒转过来，即把第一格的AAA式和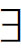A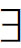式当作公理，加上在化归过程中所使用的其他辅助假定，三段论就被公理化了。因此，亚里士多德的三段论还原学说实际上是他的公理化实践，当然其中不完善之处甚多。

欧氏几何和阿基米德静力学把亚里士多德初步总结出的公理化方法真正付诸实施。欧几里德在著名的《几何原本》第一部分的开头，就给出了关于点、线、面、平面、圆等23个概念的定义，例如“点是没有部分的那种东西”，“线是没有宽度的长度”，“直线是与其中各点看齐的线”，这实际上明确了什么是欧氏几何的研究对象——现实空间。然后他先给出了5条公设，其中著名的第五公设是:“若一直线与两直线相交，且若同侧所交两内角之和小于两直角，则两直线无限延长后必相交于该侧的一点。”（这条公设通常被称为“平行公设”。）他继之给出了5个公理，例如其中第五个公理是:“整体大于部分。”从这些公理和公设出发，欧几里德演绎出了467条定理，把当时所知的全部几何学知识几乎全部推导出来了。欧氏几何是实质公理化的典范。它在给出概念、公设、公理之前，就预设了特定的对象域和论域，即由人们的感性直观所把握的现实空间，公理和公设是关于这种空间的明显事实，因而不加证明直接用作证明的前提。在选取公理和公设时，是否具有直观性和自明性也是重要的考虑标准。

欧氏几何的第五公设并不像其他公设看起来那样自明，人们一直试图从其他公理和公设中把它推导出来，从而证明它的合理性和正确性，但长时间内没有取得成功。两位数学家罗巴切夫斯基和黎曼独辟蹊径，分别用两条另外的公设代替平行公设，加到欧氏几何中去，居然得到了两种无矛盾的非欧几何——罗氏几何和黎曼几何。两种非欧几何的创立与欧氏几何不同，它们开头都没有假定任何直观背景，甚至在表面上还与直观有冲突，但两位数学家当时并不怎么理会这一点，而是埋头发展抽象的形式理论，然后在现实空间中寻找它们的解释和应用，后来两者在这方面都获得了成功，例如罗氏几何是双曲线式几何，而黎曼几何则是椭圆式几何，它们在爱因斯坦的广义相对论中得到了证实和应用。这说明，非欧几何的公理并不因其直观性和自明性而选取，但其合理性和正确性最后还是被归结于现实空间。就这一点而言，非欧几何已经开始偏离和超越实质公理化了，但仍可归属于现实世界模型。

现实世界模型长期以来也一直支配着对逻辑系统的解释。早在17世纪，莱布尼茨就提出了创立数理逻辑的理想，他要发明一套普遍语言和普遍数学，把所有的推理都化归于计算，使推理的错误成为计算的错误。在19世纪中期，布尔仿照数学中的代数演算，创立了以他自己的名字命名的逻辑代数，并允许至少三种不同的解释:类演算、命题演算和概率演算。1879年，弗雷格构造了一个被后人证明是一致且完全的命题逻辑系统和一个一致且近乎完全的谓词逻辑系统。他是一位典型的现实世界模型的倡导者和坚持者，认为只有一个世界，这就是我们所生活于其中的现实世界，它包括两部分对象:一是各种物质性客体，二是像概念、关系、命题这样的抽象实体。我们通过语言与这个世界发生关系。语言表达式都有涵义和所指，名称的所指就是该表达式在现实世界中所适用的对象。语句是一种特殊的名称，它的所指就是它所具有的真值即真或者假。逻辑是关于真理的科学，逻辑规律是关于真理的规律，是最普遍、最一般的真理，但仍然是与这个现实世界有关的真理。人们不能在该语言本身之内谈论它自己的语义学，特别是它的真概念；也不可能超出该语言本身之外去重新解释它，逻辑—语言的解释是唯一的，即参照现实世界，此外不存在任何其他的解释途径，因此任何元语言和元逻辑都是不可能的。从这些观点出发，弗雷格甚至不认为还有必要去讨论形式系统的一致性和有关一致性的证明问题。“从公理的真可以推出它们并不相互矛盾，所以根本不需要进一步的证明。”“我们有什么手段去证明某些属性、要求（或者人们愿意把它们叫做另外的无论什么东西）不相互矛盾？我所知道的唯一手段就是:指出一个具有所有这些属性的对象，给出一个所有这些要求被满足的例证。以任何其他的方式去证明没有矛盾看起来都是不可能的。” ⁽⁶⁾罗素和怀特海在《数学原理》中创立了命题演算和谓词演算，哥德尔于1930年证明了一阶逻辑的完全性，数理逻辑真正创立。如本章开头所指出的，罗素是一位典型的现实世界模型论者，蒯因在这方面更是有过之而无不及。 ⁽⁷⁾甚至哥德尔和塔斯基也持有单世界假定，例如哥德尔认为，逻辑和数学真理是客观的，是与这个现实世界相关的。 ⁽⁸⁾

对实质公理化以及现实世界模型的真正超越发生在希尔伯特的《几何基础》（1899）一书中。该书的内容可图示如下 ⁽⁹⁾:

与欧几里德的《几何原本》不同，《几何基础》一书并不预先给定对象域（如感性直观中的现实空间），对初始概念也不予定义，不给予它们任何具体涵义，公理只是初始概念的隐定义，表示的是初始概念之间的形式结构关系，选取公理的标准也不是所谓的直观性和自明性，而是推出定理时的有用性以及相对于其他公理的独立性。这样一来，在形式公理系统构成之后，就可以给其中的符号和公式以不同的解释，从而刻画不同的对象域。正是在这一意义上，希尔伯特指出:在一切几何命题中，“我们必定可以用桌子、椅子和啤酒杯来代替点、线、面” ⁽¹⁰⁾。正因为如此，《几何基础》一书构成了从现实世界模型向更为抽象的可能世界模型过渡的一个关键性环节。

2.抽象、一般的模型

在抽象、一般地考虑形式系统的解释或模型时，通常分两步进行:第一步是为该系统的形式语言指定论域，并给出形式语言内个体常项、函数符号、谓词符号在该论域中所分别代表的特指个体、函数运算以及性质或关系，这些结合在一起组成一个结构。第二步是在此结构的基础上再指定个体变项所代表的个体，这称为指派。一个结构加上结构上的一个指派才构成一个完整的语义解释（亦称赋值）。下面以一阶语言L的解释为例，一般地说明结构、指派、满足、解释（赋值）、模型、真、假、逻辑有效等重要的语义学概念。

L的一个结构是一个有序对U＝D，τ＞，其中

（1）D是非空集合，称为结构U的个体域，记为｜U｜；

（2）τ是定义在L的非逻辑符号集上的一个映射，使得:

（i）对于L中的个体常项c，τ指派D中的某个特定个体；

（ii）对于L中的n元函项符号f_ni，τ指派D上的n元运算；

（iii）对于L中的n元谓词符号F_ni，τ指派D中个体的性质（当n＝1时）或个体间的n元关系（当n＞1时）。

L的结构确定之后，L的任何一个不含个体变项的公式就有了确定的意义，并有了确定的真假。但是，对于一个含个体变项的L公式，还需要对其中的个体变项作出解释。于是，我们有:

结构U上的一个指派是指这样一个映射ρ:｛x₁，x₂，x₃，…｝→｜U｜

即是说，ρ对L中的每一个个体变项x_i（i≥1），ρ指派D中的某个个体。

然后，把结构U和指派ρ组合起来，就得到L的一个完整的语义解释:

一个L赋值（亦称解释）是指这样一个有序对σ＝U，ρ＞，其中U是一个L结构，ρ是U上的一个指派。

在赋值σ下，任一L项t或公式α都获得了确定的值，我们用σ（t）和σ（α）表示t或α在赋值σ下的值。若用u^σ表示非逻辑符号u在σ＝U，ρ＞下的值，也就是由U中的τ指定给u的值，则任一L项t在赋值σ下的值σ（t）可递归定义如下:

（i）对于L的任一个体变项x_i，σ（x_i）＝ρ（x_i），i≥1。

（ii）对于L的任一个体常项a_i，σ（a_i）＝（a_i）^σ，i≥0。

（iii）对于L中的f_ni（t₁，…，t_n），σ（f_ni（t₁，…，t_n））＝（f_ni）σ（σ（t₁），…，σ（t_n）），其中f_ni是L中的n元函数运算，t₁，…，t_n是L的任一项，i，n≥0。

由于公式的值是真值，我们用｛T，F｝代表真值集，其中T代表真，F代表假。于是，任一L公式α在赋值σ下的值σ（α）可递归定义如下:

（i）σ（F_ni（t₁，…，t_n）＝T当且仅当σ（t₁），…，σ（t_n）＞∈（F_ni）^σ，即是说在D中σ（t₁），…，σ（t_n）具有（F_ni）^σ关系。

（ii）σ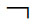（B）＝T当且仅当σ（B）＝F。

（iii）σ（A→B）＝T当且仅当σ（A）＝F或者σ（B）＝T。

（iv）σ（（Ax_i）A）＝T当且仅当每一个与之i等价的赋值σ′，σ′（A）＝T。这里，两个赋值σ和σ′是i等价的，是指对于每个j≠i，都有σ（x_j）＝σ′（x_j）。也就是说，赋值σ和σ′除可以对个体变元x_i指派不同的值（即σ（x_i）和σ′（x_i）可以不同）以外，对其他任何个体变项，σ和σ′都指派相同的值。

在这样的赋值σ之下，L的每一公式都具有了确切的涵义，并且具有了确定的真值。如果有赋值使一个公式为真，我们称该公式为可满足的；如果一公式对于任意结构中的任意指派（即任意赋值）都是真的，我们称此公式为常真公式，或普遍有效式，或永真式。反之，如果一公式对于任意结构中的任意指派都是假的，即没有任何赋值使其为真，则称它为矛盾式，或不可满足式，或永假式。显然，常真公式总是可满足的，而矛盾式则总是不可满足的。

于是，一个形式系统内的公式相对于某些确定的或任意的解释（赋值），就被区分为（1）可满足的，（2）不可满足的，（3）逻辑有效的（逻辑有效的公式都可满足）。通常把使某一公式为真的那个（或那些）解释称为该公式的模型，因此，凡可满足的公式至少有一个模型；凡不可满足的公式没有任何模型；凡逻辑有效的公式有不止一个模型。同理，相对于某些或任意的解释来说，公式集也可以区分为（1）可满足的，（2）不可满足的，（3）逻辑有效的。一公式集是可满足的，当且仅当，至少有一个特定的解释使得此公式集中的所有公式同时为真；一公式集是不可满足的，当且仅当，没有任何解释使得该公式集中的所有公式同时为真；一公式集是逻辑有效的，当且仅当，任意的解释都使得该集内的所有公式同时为真。同理，使得一公式集为真的解释被称为该公式集的模型，因此可满足的公式集有模型，不可满足的公式集无模型，逻辑有效的公式集有不止一个模型。

实际上，一形式系统就等同于它的可证公式集。于是，对于形式系统，我们可以考虑下述问题:它的可证公式集是可满足的还是不可满足的？抑或是逻辑有效的？如果一形式系统的全部可证公式都是逻辑有效的，则称该系统是可靠的。由于可靠的形式系统有不止一个模型，假如它的所有模型都同构的话，则该系统又是范畴性的。反过来，如果凡逻辑有效的公式都是某一形式系统的可证公式，则称该形式系统是完全的。既可靠又完全的系统是最令人满意的。已经证明，一阶逻辑系统K就是一个这样的系统。(www.xing528.com)

3.可能世界模型

对于持单世界假定的论者来说，语言及其逻辑的解释是唯一的，并且是确定不变的。而对于持多世界假定的论者来说，语言及其逻辑的解释是可以变换的，原则上可以给一个语言及其逻辑以多种不同的但具有等价效力的解释。这一点在现代模型论的发展中得到了最充分的体现，因此多世界假定又被称为模型论传统。这一传统特别关注语句与它的模型之间的关系，特别是语句的“真”（truth）这一概念，例如“真”在一语言内的可表达性和可定义性，等等。对于这一个传统作出重要贡献的逻辑学家和哲学家有莱布尼茨、布尔、施罗德、勒文海姆、哥德尔、后期卡尔纳普、（在某种意义上包括）塔斯基，以及后来的亨迪卡、克里普克等人。

莱布尼茨是“多世界理论”的首倡者和最明确的表述者，他提出了一个关键性概念——“可能世界”，并基于这一概念提出了一些十分重要的思想。他认为，一个事态A是可能的，当且仅当A不包含逻辑矛盾。一个由事态A₁，A₂，A₃，…形成的组合是可能的，当且仅当A₁，A₂，A₃，…推不出逻辑矛盾。由无穷多的具有各种性质的事物所形成的可能的事物的组合，就是一个可能世界。有许许多多的可能世界，例如现实世界就是一个可能世界，它是由上帝选择的一个最丰富、最完美的可能世界。他进而利用可能世界去讨论必然性、可能性、偶然性等问题，例如他认为:

D₁ 一命题是必然的，当且仅当它在所有可能世界中都是真实的；

D₂ 一命题是可能的，当且仅当它在某些可能世界中是真实的。

在他那里，逻辑真理大致相当于推理的真理，也就是在所有的可能世界中都真的真理。

20世纪50年代至60年代，鉴于模态逻辑发展的迫切需要，一批逻辑学家如坎格尔、蒙塔古、普赖尔、亨迪卡和克里普克等人从莱布尼茨的上述思想出发，发展了一种模态语义理论即可能世界语义学，从而使模态逻辑的发展进入到一个新的时期。相对于经典语义学和莱布尼茨的思想而言，可能世界语义学有几个重大的改进，具体来说:

第一，它使命题的真假相对化。由于经典语义学（隐含地）是相对于现实世界而言的，因此其公式的真假只是在现实世界中的真假，它就没有必要特别指明此公式在现实世界中真，彼公式在现实世界中假，而可以抽象地、一般地谈论其公式的真假。而在模态逻辑中，我们所面对的是各种各样的可能世界，它们之间是有某种差异的，一个体可以在一可能世界中存在，但并不在另一可能世界中存在；一事件可以在一可能世界中发生，但不在另一可能世界中发生。于是，描述或反映该个体或事件的命题就有可能在一可能世界中真，但在另一可能世界中假。这样，我们不再能够抽象地、一般地谈论命题的真假，而只能谈论命题在特定的可能世界中的真假，即是说，命题的真假是相对于特定的可能世界而言的，给命题赋值必须注明是在哪个可能世界之中。由此造成的后果是:

第二，它使必然性、可能性概念相对化。由于必然性、可能性概念是与命题的真假密切相关的，甚至是用后者定义的，既然后者是相对于特定的可能世界而言的，前者因此也就是相对于特定的可能世界而言的。我们不能再抽象地、一般地谈论必然性、可能性，而只能在某一特定的可能世界中谈论必然性和可能性；我们不能再一般地说某一命题是必然的或可能的，而只能说，某一命题在某一特定的可能世界中是必然的或可能的。

第三，它使可能世界之间具有一定的关系。命题p在一个可能世界中是必然的，不需要它在所有的可能世界中真，而只需要它在与该世界有关的所有可能世界中真。如果某些可能世界与该世界没有关系，即使p在那些可能世界中假，p在那个世界中仍然可以是必然的；但是，假如p在某个与该世界有关系的可能世界中假，则p在该世界中就不再是必然的。因此，一命题在某一可能世界中的必然性，是相对于与该可能世界有关的所有可能世界而言的。于是，D₁和D₂分别必须被重新表述为:

D′₁ 一命题在某一可能世界中是必然的，当且仅当，它在与该可能世界有关的所有可能世界中都是真的；

D′₂ 一命题在某一可能世界中是可能的，当且仅当，它在与该可能世界有关的某些可能世界中是真的。

实际上，可能世界语义学就是将上述思想精确地刻画出来，这是通过模型方法实现的。 ⁽¹¹⁾

模型是可能世界语义学的基本概念，它是一个有序三元组〈W，R，V〉，其中W是一个非空集合，R是定义在W上的二元关系，V是一个赋值。更具体地说，W是由可能世界组成的一个非空集合，W的元素当然是各个不同的可能世界w_i，w_j，…，w_n（i，j，…，n≥1）。这里要指出的是:任一抽象元素，只要能够确立任一命题在其中的真值，不管它还具有什么其他性质，都可以被看作是一个可能世界。R是定义在W上的任一二元关系，通常被称为“可通达关系”（accessibility relation），w_iRw_j因此被说成是w_i可通达到w_j。从直观上说，w_iRw_j是指w_i可以演变为w_j，如目前有核武器的世界演变为没有核武器的世界，或演变为使地球毁灭的世界。但在可能世界语义学中，R可以是W的元素之间的任一二元关系，只要它满足下述条件:如果□p在w_i中真，则p在w_j中也真，则我们就可以说w_iRw_j。V是一个赋值，它使模态公式与W中的可能世界挂钩，从而使模态公式α在W中的某个世界中为真或为假。我们下面用V（α，w_i）表示公式α在可能世界w_i中的真值，并用V（α，w_i）＝1表示α在世界w_i中为真；V（α，w_i）＝0表示α在世界w_i中为假；再引入μ作为模型〈W，R，V〉的缩写。至此，我们可以定义模态命题的真值条件如下:

（1）对任一命题变项α，V（α，w_i）＝1当且仅当V（α，w_i）≠0；

（2）V（﹁α，w_i）＝1，当且仅当，V（α，w_i）＝0；

（3）V（α∧β，w_i）＝1，当且仅当，V（α，w_i）＝V（β，w_i）＝1；

（4）V（α∨β，w_i）＝1，当且仅当，V（α，w_i）＝1或者V（β，w_i）＝1；

（5）V（α→β，w_i）＝1，当且仅当，V（α，w_i）＝0或者V（β，w_i）＝1；

（6）V（α→β，w_i）＝1，当且仅当，V（α，w_i）＝V（β，w_i）；

（7）V（□α，w_i）＝1，当且仅当，（Aw_j）（w_iRw_j→V（α，w_j）＝1）；

（8）V（◇α，w_i）＝1，当且仅当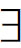，（w_j）（w_iRw_j并且V（α，w_j）＝1）。

更直观地说，（7）的意思是:□α在可能世界w_i上为真，当且仅当，α在w_i可通达的所有可能世界w_j上为真；（8）的意思是:◇α在可能世界w_i上为真，当且仅当，α在w_i可通达的有些可能世界w_j上为真。

在此基础上，我们可以定义有效性。上述的（1）至（8）是在定义“在某个模型的某个可能世界上为真”，这常被称为“满足”，所以“V（α，w_i）＝1”常被读作“α被模型μ中的可能世界w_i所满足”。α可以被某个可能世界满足，但不被另一个可能世界满足。如果α被模型μ中的所有可能世界满足，则称α在该模型下有效，该模型因此被称为α的模型；反之，如果模型μ中有可能世界使得α为假，则称此模型为α的反模型。如果α在由满足一定条件的所有模型所组成的模型类的每一个模型中为真，也就是说，α在该类的每一个模型的每一个可能世界上为真，则称α在该模型类中有效。若一模态公式在由任一模型所组成的模型类中有效，这种有效性被称为逻辑有效性，或普遍有效性。所有的命题逻辑重言式都具有这种有效性，并且在后一章第一节中提到的K公式也具有这种有效性，它在由任一模型所组成的模型类中有效。但是，公式D、T、4、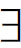、B并不具有这种有效性，它们都可以找到相应的反模型。

实际上，模型μ＝〈W，R，V〉的不同主要在于给关系R附加的条件不同，不同模型中R可能会有不同的性质。例如，关于R可以有如下定义:

R1延续性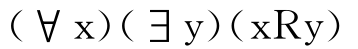　　

R2自返性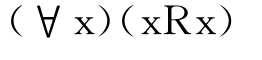　　

R3对称性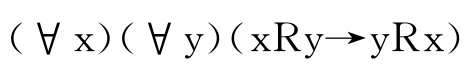　　

R4传递性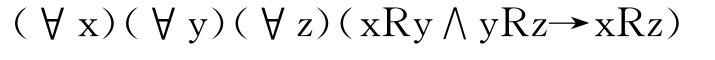　　

其中R满足R1的模型叫做延续模型，R满足R2的模型叫做自返模型，R满足R2和R3的模型叫做自返且对称的模型，R满足R2和R4的模型叫做自返且传递的模型，R满足R2、R3、R4的模型叫做自返、对称且传递的模型。可以证明，公式D、T、B、4、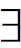分别在延续模型类，自返模型类，自返且对称的模型类，自返且传递的模型类，自返、对称且传递的模型类中是有效的。

如果一个模态逻辑系统的所有定理都在一给定模型类的每一个模型中有效，则称该系统相对于该模型类是可靠的。可以证明，K系统相对于任一模型类，D系统相当于延续模型类，T系统相当于自返模型类，B系统相当于自返且对称的模型类，S4系统相当于自返且传递的模型类，S5系统相当于自返、对称且传递的模型类是可靠的。

相反，如果在一给定模型类中有效的公式都是一模态系统的定理，则称该模态系统相当于该模型类是完全的。可以证明，K系统相对于任一模型类，D系统相当于延续模型类，T系统相当于自返模型类，B系统相当于自返且对称的模型类，S4系统相当于自返且传递的模型类，S5系统相当于自返、对称且传递的模型类是完全的。

如果一个模态系统相对于某一模型类既是可靠的又是完全的，则称该系统为那一模型类所刻画，或者说，该系统为那一模型类所决定。由于系统K、D、T、B、S4、S5对于各自的模型类来说，都是既可靠又完全的，因此它们都为相应的模型类所刻画。

以上所述的是模态命题逻辑的语义学。与模态命题逻辑相比，模态谓词逻辑中（可能）增加了个体常项、个体变项、谓词常项、谓词变项、等词、原子公式以及量化公式等。因此，对于模态谓词逻辑的语义学来说，问题是如何解释这些增加的成分。逻辑学家们已经为模态谓词逻辑系统构造语义学，并且已经证明:模态谓词逻辑系统K＋BF，D＋BF，T＋BF，B＋BF，S4＋BF，S5＋BF分别对于任一BF模型类，延续BF模型类，自返BF模型类，自返且对称的BF模型类，自返且传递的BF模型类，自返、对称且传递的BF模型类，是既可靠又完全的，它们全都为相应的模型类所刻画。

可能世界语义学为模态逻辑提供了十分适用的语义工具，它使似乎无从下手的模态概念得到了与直观十分吻合而又简单明了的解释，并证明了几乎所有模态逻辑系统的可靠性和完全性。不仅如此，它还在哲学逻辑的广大领域，例如在道义逻辑、时态逻辑、认识论逻辑、反事实条件句逻辑、一般内涵逻辑甚至优先逻辑中获得了成功的应用，当然要作一些必要的改变。它甚至还适用于经典逻辑，也可以把经典逻辑语义学作为特例包含在自身之中。例如，在詹斯·奥尔伍德等人合著的《语言学中的逻辑》中，作者就是用可能世界语义学来表述经典命题逻辑和谓词逻辑的语义学的，命题的真假也是相对于可能世界来定义的。在用可能世界语义学表述经典逻辑语义学时，只需要把模型〈W，R，V〉中的R限制为空关系，该模型就完全适合于刻画经典逻辑公式的语义特性，经典逻辑的规律就在每一个可能世界内都成立。这恰好符合我们对于可能世界的直观理解:可能世界就是不包含逻辑矛盾的世界，也就是经典逻辑规律在其中成立的世界。同时这也揭示了经典逻辑与单世界假定的内在关联:说明经典逻辑的真只需要一个一个的可能世界，而不需要涉及这些世界之间的相互关系。既然只需考虑一个一个的世界，也就可以只考虑现实世界。可能世界语义学的意义甚至远远超出了逻辑领域，而在现代哲学领域中获得广泛应用。可以这样说，在分析和探讨意义和指称问题、真理问题以及某些认识论问题，例如先验命题与后验命题、分析命题和综合命题、必然命题和偶然命题的传统区分时，不接触到可能世界语义学的概念和思想，在当代哲学中几乎是不可能的。