美国男性身高分布：钟形曲线

前阵子我和朋友汤姆去赌场玩。我们走到赌桌边时，他说：“我有一种可以在轮盘赌中赌赢的可靠办法。”我问他是什么办法，他说：“在黑色或红色上下赌注，如果赢了，就把钱拿走并再次下同样的赌注。如果输了，就在下一转将赌注加倍。想想看，你不会连续输太多次的。排除赌场优势，有接近50/50的几率——因此你很快就会赌赢。而且，就算你连输了几次，你也会在赢的那一局上一举挽回你之前的全部损失还有盈余。所以你不会输的！”这种方法听起来棒极了，因此我们把各自口袋里每一分钱都掏了出来，拼凑出400美元左右来到赌桌前。第一转时，我们在红色上下了5美元赌注，输了。我们毫不气馁，将赌注加了倍，在红色上下了10美元的赌注。结果又输了。然后我们再次将赌注加倍，下了20美元的赌注在红色上，还是输了。汤姆说：“我们不会每次都输的。”因此我们在红色上下了40美元的赌注——又输了。我们认为这种状况该结束了，于是在红色上又下了80美元的赌注，还是输了。最后，我们投进了160美元，却失望地看着球落在黑色上。我们亏掉了大部分钱，只好郁闷地离场。

为什么这种方法并不总是奏效？看起来似乎应该有用的啊。为了弄清楚原因，我们必须意识到，世界上大多数事情都是有一定的分布规律的。我说的分布规律是什么意思呢？考虑美国所有男性的身高，多数人的身高在5.8英尺至6英尺之间，少数人高于6.8英尺或低于4.8英尺。如果将处于各个身高段的男人的人数用图形表示，我们会看到一张类似图4的图。这是一种常见的分布形态，称为钟形曲线。该分布曲线的中点相当高，说明那个身高的人较多，而两端很低，说明这些身高的人少得很。当我们考虑到偶然性时，形状类似钟形的分布曲线是有意义的，因为它们说明了很多衡量方法中都有极端的情况，称为离群点。因此，如果你观察任何个别情况时，你会仅仅因为偶然而遇到离群点。如果你从美国随便选择一个男人，他可能有7英尺高，也可只有4英尺高。

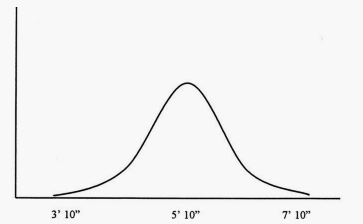
图4　钟形曲线：假想的美国男人身高分布图示例

这与我们在轮盘赌桌上的惨败有什么关系呢？我们忘记了赌场优势（球落在0或00上），落在红色或黑色上的概率类似于抛硬币。抛硬币时得到正面（或反面）的概率是0.5，因为只有两种可能的结果。连续两次正面朝上的概率是多少？是0.5×0.5，即0.25。也就是说，有25%的几率连续出现两次正面朝上的情况。从下面的结果组合中可以看出这一点，其中H和T分别代表正面和反面：

HT，TH，HH，TT

由于有4种可能的结果，因此HH有四分之一的发生几率（25%）。现在推理抛6次硬币的情况。要计算连续出现6次正面朝上的概率，只要将0.5自乘6次，结果是1.56%。因此对于任何一组抛6次硬币的情况，连续出现6次正面朝上的概率大约是1.5%。虽然概率很低，但这种情况也是会出现的。对于任何给定的连抛6次事件，这种情况出现的概率比不上3正3反或4正2反之类，但仍然是有可能发生的。事实上，如果我们进行很多组6次连抛，很有可能发生这种情况。例如，如果做1000组连抛6次，可以仅仅根据概率就预料到全部正面朝上的有15组（1000×1.5%）。轮盘赌也是如此。如果轮盘转几千次，情况肯定不一样，汤姆和我只是运气不好，才连续6次都碰到球落在黑色上。遗憾的是，我们在球落到红色数字上之前已经囊中羞涩。

因为人们认为这些极端事件不大可能发生，所以常常将这些事件归因于其他一些神秘原因。他们可能以为抛硬币或转轮盘的人有某种控制结果的特殊力量。然而，在将某个事件归因于其他可能的原因（比如通灵或神秘力量）之前，必须确定这些力量是否能使事件的发生超出根据概率所计算出的期望值。正如我们所看到的，如果进行一千组6次硬币连抛，根据概率就可以预期大约会有15组都是正面朝上。在我们相信是某人的通灵力量导致连续6次正面朝上之前，他必须能演示在1000组抛硬币过程中产生远远超过15组正面朝上的现象。如果没有，那么6次都正面朝上可以用概率来解释。

分布图尾部明显的极端情况导致很多人形成了错误的信念。假设你的朋友被告知他得了严重的癌症，预计他这种情况的平均寿命只有一年多。得到这样的消息后，有些病人会尝试奇奇怪怪的治疗技术，比如治疗式触摸、水晶治病，甚至通灵手术。有些病人可能活得超过了一年，如果是这样，他们通常认为这是另类治疗技术延长了他们的生命。但是寿命分布图中也有变异，虽然患这种癌症的病人的平均预期寿命可能为一年，但有人可能一个月后死亡，而其他人可能又活了五年。从本质上讲，分布图的尾部表明有人会活得远远超过平均寿命，而人们在形成信念时往往会忽略这一事实。

分布图的尾部也说明了要听取资深专家的共识，而不是偏听个别人的意见。大多数领域都有数千名专家，很有可能其中有些专家会相信一些非常离奇的事情。甚至在科学家、教授、资深专家中也可能有“离群者”——只是一位专家这样说，并不意味着事情就一定是真的。还记得哈佛大学的约翰•麦克关于外星人绑架的离奇信念吗？如果我们寻找专家的共识，就更可能接近目前为止所能知道的真相。(www.xing528.com)

特异功能

概率论可以解释很多表面上看起来不可思议的事情。例如，考虑ESP（特异功能）的情形。迈克尔•舍默有一次去弗吉尼亚海滩的埃德加•凯西研究和启示协会，这是一个看上去很官方的做ESP实验的组织。①他到那里时，他们正在做一个实验，其中一个人（接收者）试图辨别另一个人（发送者）看到的某些形状。“发送者”将注意力集中在一张卡片上，卡片可能显示加号、方块、星形、圆形或波浪线。与此同时，要求“接收者”将注意力集中在发送者的前额上，并尝试辨别他在想什么。有35人参与了二次这样的实验，每次分别识别25张卡片。

①Shermer的Why People Believe Weird Things；也可参见Shermer的“Deviations”，Skeptic 1，no. 3（1992）：12。

指导员说每个人都有某种程度的特异功能，只不过有些人比别的人多一些。他表示仅根据概率，平均而言人们应该从25张卡片中正确识别出5张（由于有5种符号）。事实上，他说只要辨别出3~7张，用概率来解释都是准确的。然而，只要有人识别的卡片超过7张，就说他有特异功能。结果表明，在第一次试验中有3个人识别出了8张卡片，在第二次试验中有一个人识别出了9张卡片。因此，根据凯斯协会的说法，至少有4名参与实验的人没有受过特殊训练却表现出了特异功能。但是他们真的有特异功能吗？

概率论表明，因为概率的缘故，受试者的识别准确率也会有变化。虽然在第一轮试验时3个人正确地猜出了8张卡片，但是也有3个人仅猜对了两张——其他29个人正确猜出的卡片张数在3到7之间。在第二轮试验中，有一个人猜对了9张，但是有3个人仅正确地猜对了2张或1张（都不是第一组中得分特低和特高的人），其余的人猜对的都在3到7张之间。还记得之前讲过的钟形曲线吗？这些结果看起来非常像一个正态钟形曲线分布，平均值大约是猜对5张，围绕该平均值又有一定的偏差。因此，根据概率可以预料到有些人会猜对8张或9张。事实上，如果有一大群受试者，我们可以预料到有人的分数会更高。总而言之，概率论已经预测到了这些结果类型，因此不需要借助特异功能之类的神秘原因来解释这个实验。

据舍默说，当他向团体提到钟形曲线时，指导员说：“你是工程师呢，还是搞统计的，还是别的什么人？”②大家都哄笑起来，指导员则继续回到讲台上讲如何提升他们的ESP。当想要相信某事时，我们会忽视、淡化甚至嘲笑与之矛盾的解释。如果对概率缺乏很好的理解，就较有可能发生这种情况。事实上研究人员发现，相信ESP的人不如不相信的人那么懂得概率，因此他们更有可能将极端事件归因于超自然解释。③

②Shermer，Why People Believe Weird Things第70页。

③S. Blackmore，“Belief in the Paranormal：Probability Judgments，Illusion of Control，and the Chance Baseline Shift”，British Journal of Psychology 76（1985）：459；S. Vyse，Believing in Magic：The Psychology of Superstition（New York：Oxford University Press，1997）第102页。