长三角经济区：空间划定与Zipf定律实证研究

第八章　经济区域空间划定以及经济区域内Zipf定律的实证研究——以长三角经济区为例

Zipf定律揭示了包含在不同区域空间层次上城市人口规模的规律分布，一直是区域经济学、城市经济学以及地理经济学的研究热点之一。有关Zipf定律的实证研究的区域空间层次一般基于国家层次，其逻辑是：一国公民可自由迁徙到任何城市就业定居，且流动到境外去只占人口的极小比例。因此选择国家层面是非常自然的。

都市圈或者更广义的经济区域的空间划定一直以来也是区域、城市以及地理学界研究的中心问题之一，基于各种空间相互作用的实证研究极其丰富。我们有个猜测：一个合理划定的相对独立、完整的经济区域，该区域人口主要在其内部流动，也许处于该区域内部的城市的人口规模的分布也会展现出类似整个国家层面的规律性。

第一节　方法和数据

一、模型的设定

城市之间的经济联系是一个综合的概念，经济联系可以细分为人员流、货物流、资金流、信息流等，城市之间经济联系强度的大小，也就是相互作用的强弱，可以直观地用人员、货物、资金、信息等联系数量的大小来表现。计算两个城市经济联系强度的典型公式是：

其中：Rij是两城市经济联系强度；Mi、Mj分别是始点和终点城市的规模指标，有的取人口规模指标，也有的取经济规模指标比如GDP，或者取几个综合总量经济指标的加权平均值；Dij是两城市的经济距离；k为常数。这一经济联系的量化模型建立于诸多假设之上，例如各城市经济活动相似，城市辖区内的经济活动集中于代表该城市的那个点，城市间经济联系方式相似，没有巨大的制度或者地理上的障碍等等。当然，这个算式中的指数的设定是经验假设，需根据具体情况进行修正。考虑到城市之间经济结构等方面的不同，可以将经典的引力公式拓展如下：

其中：Ωij是城市i和城市j的经济结构差异度。

公式（2）算出的是潜在的经济联系强度。可观测的现实的经济联系强度可表述如下：

其中：Pf lowij是城市i和j之间的人员流动量；Fij是城市i和j之间的货物流动量；Iij是城市i和j之间的包括资金、有经济意义的信息流（比如生产技术、专利等的流动）等的总量。然而，现实中两城市之间的货物流、资金信息流的准确数字极难得到，能得到的比较准确的数字是人员的流动量。假设人员的流动量与现实的经济联系强度有某种比例关系，而现实的经济联系又与潜在的经济联系有某种比例关系，则最终两城市间潜在的经济联系强度与两城市间的人员流动量存在某种比例关系。因此，可用能观测到的城市i和j之间的人员流动量Pf low ij作为无法直接观测的城市i和j之间的潜在经济联系强度Rij的代理变量。这样，（2）可以近似表示为

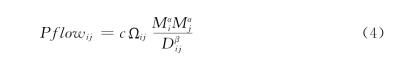
以往研究已经证实了城市体系内部分形的存在，因而我们可以合理地假设城市i是中心城市，地理空间比较靠近的城市存在相似性，或者说有某种分形现象存在。另外，假设两个空间上比较靠近的非中心城市j和k，经济结构相似，也就是说与中心城市的经济结构差异度相似，即Ωij＝Ωik，则中心城市与非中心城市之间的人员流动量Pf lowij可以化简为

其中：K＝cΩij是与中心城市i相关的常数。

对（5）两边取对数，得

利用（6），我们可以估计出未知的参数α和β。未知的参数α和β估计出来之后，我们就可以返回去利用（2）将两城市间潜在的经济联系强度算出来。

更进一步，个体市i的经济地位或者重要性可用潜能Gi来表示：其中：n是经济区域内所有城市的数目。

为了确定哪些城市应该划入某个大城市为中心城市的经济区域，我们可以定义Limax为城市i的最大经济联系：

在计算城市i的最大经济联系时，应视为以城市i为中心，半径为它与预先假定的中心城市之间的直线距离，与它发生经济联系的城市包含在这个圆内，逐一计算它与这些城市的经济联系，然后找出最大者。

以某大城市为中心城市的经济区域的划定原则可阐述如下：（1）如果城市i的最大经济联系L maxi是和城市j发生的，而且Gi小于Gj，则城市i经济上附属于城市j（或称城市j是城市i的上级城市）；

（2）如果城市i经济上附属于城市j，而城市j经济上又附属于城市k，则城市i也附属于城市k；

（3）如果一个城市不附属于任何其他城市，则该城市为该区域的中心城市。

根据以上原则，如果我们能确定某个城市为中心城市，则以该城市为中心城市的经济区域也大致可以确定了。

整个经济区域划定后，我们就可以进行该区域内Zipf定律的验证和检验了。

我们拟采用以下公式

其中：P（i）是该经济区域内所有城市人口规模按从大到小降序排列的排第i位的人口数。

二、变量的选取和数据来源

1．变量的选取

在计算两个城市潜在的经济联系强度时，城市的规模指标通常选取城市（或市区）的人口规模、GDP、市区工业生产总值或者几个综合总量经济指标的加权平均值。由于人口规模相对GDP是更全面的指标，我们选取城市市区总人口（变量命名为POP）作为体现城市规模的指标。另外，城市的经济距离我们选取两城市市区之间的公路里程数（变量命名为DIS）。以往研究有取两城市间的公路里程数，也有取公路和铁路里程的加权平均数的，还有取两城市间来往所需时间的。如果取公路里程数，可能不全面，因为经济区域通常跨越省界，省际交通方式不仅包括长途汽车，还包括铁路和航空，甚至还有水运。如果选择这些不同交通里程的加权，由于这些不同交通方式的里程数以及被使用的频数都是不同的，需要加权。要确定比较准确的权数，除不同交通方式的里程数之外，还需要采用这些不同交通方式的乘客的相互比例关系。这需要非常庞大的数据量，比较难处理。取两城市间来往所需时间也会碰到加权的难题。由于长三角城市之间的货物流动主要是通过公路，因此城市之间的经济距离主要是公路里程，而且公路里程和铁路里程差别较小。综合以上考虑，我们就取两城市间的公路里程数作为两城市间的经济距离。

在经济区域划定时，我们只选取地级市及以上的城市，采用经济区域划分中的递归原则：如果某个地级市经济上隶属于另一个更大的城市，则这个地级市所属的更小的城市也在经济上隶属于这个更大的城市，而一般来说该地级市所辖县级市不仅在行政上有隶属关系，在经济上也同样存在隶属关系。在经济区域划定后验证Zipf定律时，由于县级市没有关于县城的人口统计，只统计了整个县的人口，但是县级市总人口则除部分非农业人口集中在县政府所在的县城外，大部分人口则分散在农村，所以我们只选取地级市及以上的城市。对地级市及以上的城市的人口我们选取城市市区总人口数（包括了非农业人口和农业人口）。

2．样本的确定及数据的来源

以往关于经济区域或都市圈的实证研究显示：如果以中心城市为圆心，其半径一般在300—400公里。我们预先假定上海为中心城市，半径取上限400公里。凡是离上海的直线距离在400公里之内的地级市及以上的城市都是候选城市。候选城市包括上海、江苏、浙江以及安徽总计30个城市：上海；南京、扬州、泰州、镇江、常州、无锡、苏州、南通、盐城、淮安（10个）；杭州、嘉兴、湖州、绍兴、宁波、舟山、金华、台州、丽水、温州、衢州（11个）；滁州、马鞍山、芜湖、宣城、铜陵、池州、黄山、巢湖（8个）。当然，处于这个区域的边缘城市，也会和被预先划定在区域之外的城市发生经济联系。在计算和比较边缘城市的经济联系时，也要把边缘城市与区域外城市的经济联系考虑在内。处于边缘的小城市会同时受到区域外的大城市的吸引和区域内大城市的吸引。如果这些边缘城市经济联系强度最大者在区域内，则划入经济区域；如其经济联系强度最大者在区域外，则从经济区域内划出去。同样，处于事先人为划定的区域之外的边缘城市也会受到区域外的大城市以及区域内的大城市两方面的吸引。如果这些区域之外的边缘城市其经济联系强度最大者在区域内，则划入该经济区域；如其经济联系强度最大者在区域外，则仍是区域外城市，不划进来。如果利用这种方式最终能够确定上海确实是长三角的中心城市，则我们的预先假定是成功的。

关于上海与区域内其他城市之间的人员流动量我们采用了与王维和罗守贵（2006）类似的计算方法。从上海到区域内其他城市的人员流动采用空运和水运方式的相当少，主要是通过公路客运和铁路客运，所以计算人员流动量时就没有考虑空运和水运。通常长途客车载客量为50人，而列车一节车厢满员是118人。铁路客运沿途停靠站点较多，要分情况讨论。根据对铁路车票预售在起点站、中途停靠站以及终点站之间分配情况的调查，作如下处理：B1：上海为始发站，目标城市为终点站的列车班次，设定其中有5节车厢的乘客去往目标城市；B2：上海为始发站，目标城市非终点站的过境列车班次，设定有2节车厢的乘客去目标城市；B3：上海非始发站，目标城市为终点站的列车班次，设定其中有1．5节车厢的乘客去往目标城市；B4：上海非始发站，目标城市非终点站的过境列车班次，设定其中有1节车厢的乘客去往目标城市。这样我们可以得到：

上海与区域内某城市间人员流动量＝两市间公路人流量＋两市间铁路人流量＝［50A＋（6B1＋2B2＋1．5B3＋B4）×118］×365（10）

根据实际的车次统计，代入上式，得到人员流动量如表4‐8‐1。

表4-8-1　上海与区域内其他城市之间的火车、汽车班次及人员流动量

资料来源：火车班次来自中国铁路时刻表：www．shike．org．cn；长途汽车班次来自易行网：www．ewalker．com．cn
资料说明：表4‐8‐1中没有列入舟山。作为海岛城市，舟山不通铁路，长途汽车也需要通过轮渡从宁波转过去，与上海的直接交通途径只有空运和海运。

关于城市人口、城市人均GDP等数据的来源是《中国城市统计年鉴2008》、《上海统计年鉴2008》、《江苏统计年鉴2008》、《浙江统计年鉴2008》和《安徽统计年鉴2008》，两城市之间的直线距离由中国电子地图得到，两城市之间公路里程数来自中国公路信息服务网www．chinahighway．gov．cn。数据年份统一取2007年。

第二节　模型估计

一、经济区域的划定

利用软件EVIEWS6．0，采用OLS方法，对方程（6）进行估计，结果如表4‐8‐2：(www.xing528.com)

表4-8-2　方程（6）估计结果

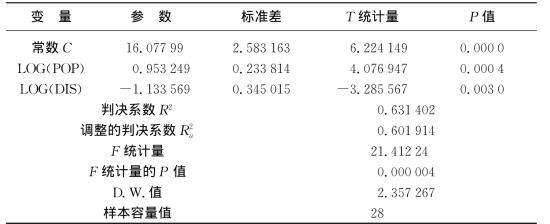
我们得到估计方程

由输出结果看，本模型可以通过α＝0．000 004的F检验，说明方程总体的线性关系极其显著，即有大于99%的可信度上海与区域内其他成员城市之间的人员流动量与其人口规模和经济距离存在密切的关系。另外，模型分别通过α＝0．0004和α＝0．003的t检验，说明每个解释变量对被解释变量来说都是显著的。

不考虑城市间经济结构的不同，即假定Ωij＝1，则利用（2）可算出任意两城市之间潜在的经济联系强度，进而计算出某城市的潜能Gi以及其最大经济联系城市。计算结果见表4‐8‐3：

表4-8-3　长三角经济区域成员城市的最大经济联系城市、潜能及其上一级城市

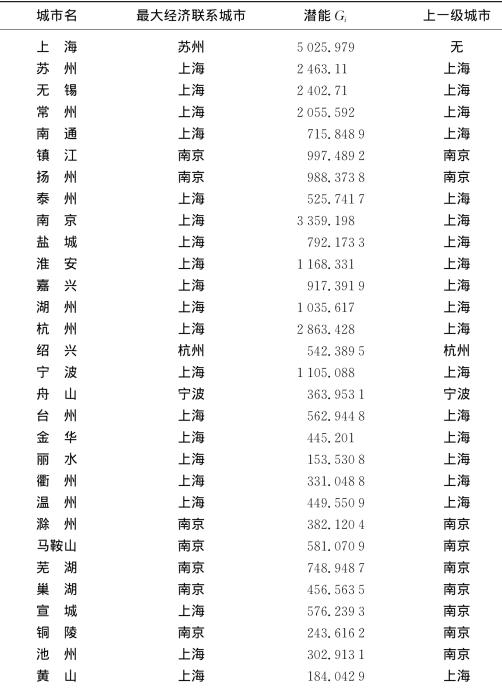
说明：尽管其他城市没有直达舟山的火车和长途汽车，但长途汽车可以先行抵达宁波再转往舟山。其他城市到舟山的公路里程数我们按其他城市到宁波的公路里程累加宁波至舟山的公路里程数59公里。由于舟山和其他城市的经济联系相比其他城市可能更多依赖于水运和空运，我们这里的计算很可能低估了舟山的潜能值（舟山的人均GDP在传统的长三角16个城市中位居中游）。另外，由于上海到舟山的经济距离是根据上海到宁波加上宁波到舟山的公路里程计算的，上海到舟山可能更多地通过水运和空运，因此这里的计算也很可能低估了舟山与上海的经济联系强度，从而很可能舟山的最大经济联系方是上海而非宁波（舟山与上海的经济联系强度只比舟山与宁波的经济联系强度低一点）。

根据经济区域的划定原则，由表4‐8‐3可以得到：上海确实是长三角经济区域的中心城市，下面有南京、杭州两个副中心城市，南京经济上隶属有镇江、扬州、滁州、马鞍山、芜湖、巢湖、铜陵7个城市，杭州经济上隶属有绍兴，其余城市经济上都隶属于上海。

如果取潜能在500以上（相对经济联系更紧密）作为长三角经济区域的成员城市，我们发现巢湖、温州、金华、滁州、舟山、衢州、池州、铜陵、黄山和丽水等10个城市将被剔除，即剩下20个城市。但考虑到舟山的特殊性，也可将舟山放入，即长三角经济区域共有21个地级及以上城市，比传统的16个城市多了淮安、盐城、马鞍山、芜湖和宣城5个城市。长三角经济区或城市群传统上包括16个城市：上海、南京、苏州、无锡、常州、镇江、扬州、泰州、南通、杭州、嘉兴、湖州、绍兴、宁波、舟山和台州。这种传统的划定除了考虑空间上的靠近，可能更多地是经济发展水平上的考量：16个城市的人均GDP比较接近。淮安、盐城、马鞍山、芜湖和宣城5个城市比16个城市中人均GDP最低的南通和泰州要低1万，与人均GDP最高的苏州、上海等城市相比差别更大。如果我们是选长江三角洲地带的富裕城市俱乐部，那么传统的16个城市的空间划定非常合理。如果更多考虑整个长江三角洲地带的协调发展，则经济发展相对落后的淮安、盐城、马鞍山、芜湖和宣城5个城市也可以考虑入选。

二、Zipf定律的验证、检验及比较

1．以单独的行政省作为一个相对独立、完整的经济区域

我们分别以浙江和江苏省作为相对独立、完整的经济区域来验证和检验Zipf定律。

对浙江省的估计结果如下：

关于帕累托系数ζ＝1的假设检验：采用系数约束的Wald检验，其P值＝0．135 1，不能拒绝关于ζ＝1的原假设。

对江苏省的估计结果如下：

关于帕累托系数ζ＝1的假设检验：采用系数约束的Wald检验，其P值＝0．069 6，在10%的显著性水平上拒绝了关于ζ＝1的原假设。

2．传统的长三角16个城市作为一个相对独立、完整的经济区域

对传统的长三角16个城市做Zipf定律的验证和检验，其估计结果如下：

关于帕累托系数ζ＝1的假设检验：采用系数约束的Wald检验，其P值＝0．019 3，在5%的显著性水平上拒绝了关于ζ＝1的原假设。

3．经由经济联系计算确定的长三角30个城市作为一个相对独立、完整的经济区域

对30个城市做Zipf定律的验证和检验，其估计结果如下：

关于帕累托系数ζ＝1的假设检验：采用系数约束的Wald检验，其P值＝0．099 2，在10%的显著性水平上拒绝了ζ＝1的原假设。

4．相比30个城市更加紧密联系的长三角21个城市作为一个相对独立、完整的经济区域对21个城市做Zipf定律的验证和检验，其估计结果如下：

关于帕累托系数ζ＝1的假设检验：采用系数约束的Wald检验，其P值＝0．539 2，不能拒绝ζ＝1的原假设。

由以上估计结果，我们可以看出：相比其他种类的、由行政区划确定的经济区域，经由经济联系计算确定的长三角经济区域其人口规模的分布比较完美地符合Zipf定律。这正好确证了我们的猜想：一个相对完整和独立的经济区域，人口在各城市间的分布也许更加符合理想状态的Zipf定律。

为验证Zipf定律是否能稳定有效地解释由这21个城市组成的长三角经济区域的人口规模分布，我们另外取1997年至2006年的这21个城市的人口数据（淮安2001年以前为淮阴，宣城2001年成为地级市，之前为县级市），估计结果如下：

表4-8-4　长三角21城市1997—2006年Zipf定律的估计及检验结果

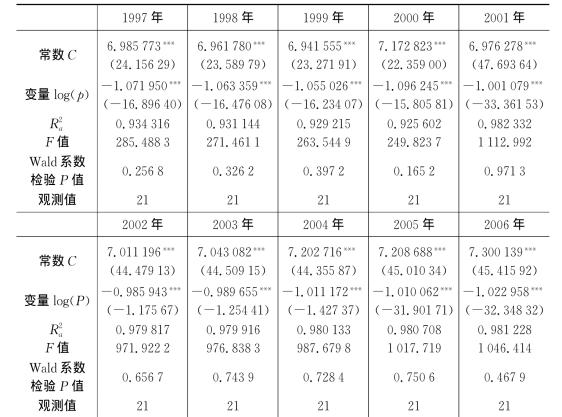
注：括号内的数字为t检验值；＊＊＊表示在1%水平上显著。

我们发现对于长三角21个城市的人口规模分布，在1997年至2007年所有年份都不能拒绝ζ＝1的原假设，由此可以得出我们计算确定的这21个城市组成的长三角经济区域的人口规模分布可以由Zipf定律得到稳定而有效地解释，或者说这可以进一步佐证我们对长三角经济区域划定的合理性。

（向永辉）

参考文献

1．许波和纪慰华：《长江三角洲地区城市规模分布的分形研究》，《城市问题》2001年第2期。

2．班茂盛和祁巍锋：《基于分形理论的浙江省城市体系规模结构研究》，《中国人口科学》2004年第6期。

3．王桂新：《中国长江三角洲地区城市化与城市群发展特征研究》，《中国人口科学》2005年第2期。

4．张虹鸥等：《珠江三角洲城市群城市规模分布变化及其空间特征》，《经济地理》2006，26（5）：806—809。

5．潘鑫和宁越敏：《长江三角洲都市连绵区城市规模结构演变研究》，《人文地理》2008年第3期。

6．许学强、周一星、宁越敏：《城市地理学》，高等教育出版社1997年版。

7．张义文等：《河北省主要城市吸引范围》，《河北师范大学学报》（自然科学版）2001年版第4期。

8．王维和罗守贵：《上海都市圈城市间引力研究及基于人流量的实证分析》，《软科学》2006年第3期。

9．顾朝林和庞海峰：《基于重力模型的中国城市体系空间联系与层域划分》，《地理研究》2008年第1期。