修订版正义论：引导平均功利原则的推理

我现在想考察赞成平均功利原则的推理。古典功利主义的原则将在后面讨论（见第30节）。契约论的一个优点就是它揭示了这两个原则是明显不同的观念，不管它们的实际推论可能多么一致。支持它们的分析性假定分歧很大，表现在它们对最初状态的解释是对立的。下面我将努力说明这一点。

在用于社会基本结构时，古典功利主义原则要求制度应安排得能最大限度地增加各有关代表人的期望的绝对总额。这一总额是通过用处于相应地位的人数来乘每一期望，然后再把结果相加达到的。这样，假如其他情况一样，当社会中的人数翻番时，整个的功利也就翻了一番（当然，按照功利主义观点，期望是对全部被观察和预见到的满足的衡量，它们并不像在作为公平的正义论中那样，仅仅是主要善的指标）。与此相对照，平均功利原则指示社会不仅要最大限度地增加功利总额而且要增加平均功利（按人分配的功利）。这看来是一个较现代的观点，密尔和维克塞尔坚持这一观点，最近另有人给它以一个新的基础。^[21]为使这一观念适用于社会基本结构，制度的建立要能够最大限度地增加各代表人的期望总额的百分比。为计算这一总额，我们用处于相应地位的社会的分数来乘以期望。这样，假如其他情况一样，当一共同体人口翻番时，功利并不一定翻番。相反，只要在不同地位中的百分比没有改变，功利就仍保持不变。

在这些功利原则中，哪一个在原初状态中将比较可取呢？为回答这一问题，我们应当注意到：如果人口数量保持不变，两者则趋于同一，但当人数变化时就出现了差别。古典原则要求：就制度影响着家庭的大小、结婚的年龄等等而言，它们应当安排得使最大的功利总额能够达到。由此得出只要每个人的平均功利在人数增加时足够慢地降低，就应当无限制地鼓励人口的增加，而不管平均功利降得如何低。在这种情况下，因人口增加而增长的功利总额足以抵偿人均份额的下降。作为一个正义的问题而非选择权的问题，一种很低的平均福利可能还是需要的（见图11）。

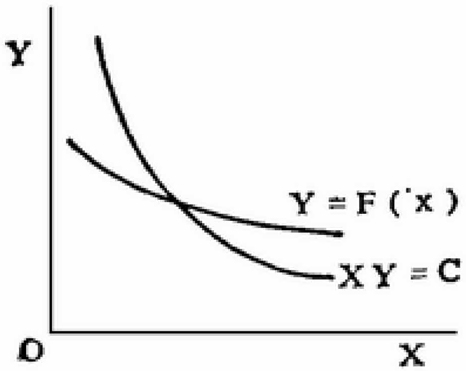
图11

人口的无限增加

形式上，无限增加的人口的条件是曲线y=F（x）（设y是人平均量，x是人口数）应当比等轴双曲线xy=C平直。由于xy等于功利总额，那么，代表这一总额的矩形面积就在曲线y=F（x）比xy=C平直的任何时候，随着x的增加而增加。

现在，古典原则的结果看来表明它将被赞成平均原则的各方拒绝。两个原则仅在假定平均福利总是下降得足够快（至少超出某一点）以致双方不再有严重分歧的情况下，才趋于相同。但这一假定是成问题的。从原初状态中人们的立场看，同意某种平均福利的最低额看来是较合理的。由于各方都旨在推进他们自己的利益，他们在任何情况下都没有最大限度地增加满足总额的欲望。因此，我假定，功利主义中可替换两个正义原则的较合理对象是平均原则而非古典原则。(www.xing528.com)

我现在想考虑各方可能怎样达到平均原则。我要概述的推理完全是一般性质的，如果它是正确的，它将完全避开怎样提出选择对象的问题。平均原则将被看作是惟一合理的候选者。让我们设想一种状态，在那里一个单独的有理性的人能够面对好几个社会而选择进入某一个社会。^[22]为明确观念，先假定这些社会的成员全部都有同样的偏爱，也假定这些偏爱满足了使一个人能够确定一种基本功利的条件。再者，每个社会都有同样的资源和同样的自然才能的分配。然而，拥有不同才能的人有着不同收入，每个社会都有一种再分配的策略，如果压力超过了某一点，它就削弱刺激，并因此降低生产。假定在这些社会里遵循的是不同的策略，一个单独的人会决定加入哪个社会呢？如果他准确地知道他自己的能力和利益，如果他有详细的有关这些社会的信息，他或许能够预见他在各个社会中几乎是肯定要享受的福利。然后他就能在此基础上做出决定，无需计算任何可能性。

但这种情况是相当专门的。让我们一步步地观察它以便不断接近原初状态的情形。这样，我们先假定这一假设的加入者对他的才能将使他在这些不同的社会里扮演什么角色没有把握。如果他推测他的偏爱也是跟别的所有人一样的，他可能按最大限度地增加他期望的福利的方向做出决定。他通过把一个社会的代表人的功利作为可供选择的功利，把他对他达到它的机会的估计作为每一地位的可能性来计算他在一个既定社会中的前景。那么，他的期望就是由代表人的一个增加的功利总额决定的，亦即由Σp_iu_i决定的，在此p_i是他达到i地位的可能性，u_i是相应的代表人的功利。然后他就选择能提供最好前景的社会。

一些进一步的修正可使这一境况更接近原初状态的情形。假设这一假定的参加者丝毫不知道他的能力或他可能要在每个社会中占据的地位。且仍然假设他的偏爱也跟这些社会中的人是完全一样的。现在我们再来假设他有成为任何一个个体的同等可能性（即，他成为任何代表人的可能性等于该代表人代表着的社会分数），因而也假设他不断沿着可能性的路线进行推理。在这种情况下，他的前景还是和每一社会的平均功利等同的。这些修正最后就使他期望在每个社会中的获利与这一社会的平均功利一致。

迄今为止我们一直假设所有个人都有相似的偏爱，不管他们是否属于同一个社会。他们的善的观念大致是同样的。一旦这一很强的假设被削弱，我们就走到了最后一步，达到了一种最初状态。我们可以说，对这些社会的成员或那个抉择者的具体偏爱我们一无所知。这些事实和对于这些社会的结构的知识都被排除了。无知之幕现在完全形成了。但我们还是能想像那个假设的新来者能像以前一样地推理。他假设有一种使他成为任何人的平等的可能性，并被充分地赋予那个人的偏爱、能力和社会地位。这再次表明，他在那个有最高的平均功利的社会里有他最好的前程。我们可以通过下面的方式看清这一点。设n是一个社会中的人数，设他们的福利水平是u₁，u₂，…u_n。那么功利总额就是Σu_i，平均功利就是Σu_i/n。假设一个人有成为任何一个人的平等机会，他的前景就是：1/nu₁+1/nu₂+…+1/nu_n或Σu_i/n。前景的价值是和平均功利相等的。

这样，如果我们放弃功利的人际比较的问题，如果各方被看作是不反对冒险和在计算可能性中遵循不充足理由原则（那个作为先前的概率计算基础的原则）的有理性的个人，那么，最初状态的观念自然就导致了平均原则。通过选择它，各方增加了从这一观点看是他们所期望的最大限度的福利。这样，契约论的某种形式就提供了一种支持平均原则而非古典原则的论证。事实上，平均原则又怎么能以别的方式解释呢？说到底，在严格意义上它并不像古典观点一样是一种目的论的理论，因此它缺少对最大限度地增加善这一观念的某种直觉诉诸。一个坚持平均原则的人至少在这个范围里会希望诉诸契约论。

而且，在考虑一个假设的新来者的立场中并不会损害到一般性。诚然，在原初状态中的人们知道他们已经在某一特定社会中占有一个地位。但是，从最初状态的观点来看，思考事情是怎样发生过的和思考事情将要怎样发生并无本质的差别。无知之幕消除了区别它们的根据。这样，无论以两种方式中哪一种方式，都能做出支持平均原则的论证。^[23]在接受这一原则时，各方将同意尽可能好地把他们的社会安排得符合于这一原则，他们将像那个在类似于原初状态的环境中选择要进入哪个社会的新来者一样运用这一原则。平均原则要求有助于那些在最初状态中的人，只要这些人被领悟为准备在所有情形中按最抽象的或然性推理冒险的单独的理性个人。为论证两个正义原则，我必须展示：那些确定原初状态的条件排除了各方的这种观念。的确，我们在此面临作为公平的正义的一个主要问题：即要以这样一种方式规定原初状态，以便即令有意义的契约终能达成（无知之幕与别的条件一起消除了交易和偏见的基础），加在达成这一结果的过程上的那些限制条件还是要引导到具有契约论传统特征的原则。