科学理论发现的逻辑方法-《当代科学技术哲学导论》试读

三、科学理论发现的逻辑方法

逻辑思维，亦称抽象思维，是在感性认识的基础上，运用概念、判断、推理等方式对客观对象作出的一种间接的、概括的反映过程，是科学认识的一种普遍的、基本的形式。科学概念、定律、原理的形成，一般都要经过抽象与概括的逻辑操作。比较、分类、分析、综合、归纳、演绎、类比等，是运用逻辑思维常见的科学方法。限于篇幅，这里仅就归纳方法、演绎方法、类比方法和思想实验分别进行讨论。

1.归纳方法

“归纳”一词，希腊文写作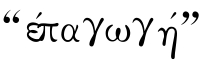⁽²⁷⁾，意思是由个别到一般的推理方法。它是在考察某类事物部分对象的基础上，抽取其共性并推广到该类的全体，从而形成关于该类对象的一般性认识。这是一种扩充性的推理，从观察到的扩充到观察不到的，从部分扩充到全体，从抽样扩充到总体。在科学认识的过程中，从经验事实上升到经验定律的最初假定，通常都是使用归纳方法的。科学中的经验定律、经验公式，大多数是通过归纳方法得到的。

通常，依据归纳概括的方式与成果的不同，将归纳分为全称性归纳法和统计性归纳法。

（1）全称性归纳法

即以全称命题的形式表述其归纳成果的一种归纳方法。也就是说，即是一种探索以全称命题陈述的经验定律的方法。全称性归纳法又可分为完全归纳法和不完全归纳法。

所谓完全归纳法，是根据某类事物的全部对象的考察，而作出关于该类事物的一般性结论的推理方法。例如，化学中关于“所有零族元素都是惰性元素”和基本粒子物理学中关于“夸克都带分数电荷”这两个命题就是运用了完全归纳法得到的。在前例中，对零族元素中He、Ne、Ar、Kr、Xe、Rn等全部的六个元素逐一加以考察，它们都具有惰性，由此概括得出所有零族元素都是惰性元素的结论。完全归纳法的根据是充分的，因为它对每一个对象作了考察，抽取其共性，然后得出普遍性结论。这种推理方式是一种必然性概括，它的必然性可以从两个方面理解。一方面从逻辑模式看，前提与结论的逻辑联系是必然的；另一方面从结论看，结论是必然真的，即结论为前提所蕴涵，只要其前提是真实可靠的，其结论也必然是真实可靠的。但是，完全归纳的创造性是极其有限的，并且这种方法只适用于被考察的对象不多的场合。当被考察的对象数量很大时，它就不可能应用，而必须求助于不完全归纳法。

不完全归纳法，即是根据某类事物的部分对象的考察而作出该类事物的一般性结论的一种推理方法。例如，天文学中描述行星同太阳平均距离的经验定律即著名的提丢斯-波德定律，就是运用不完全归纳法得到的。1766—1772年，德国数学家J·D·提丢斯和柏林天文台台长J·E·波德通过天文观测得到如表7-1所列的数据。他们由观测数据进行归纳概括，就得到第n个行星（对水星而言，n不取1，而是－∞）同太阳平均距离的经验公式：

R_n＝0.4＋0.3 × 2^n－2（天文单位）。

表7-1　通过天文观测得到的数据

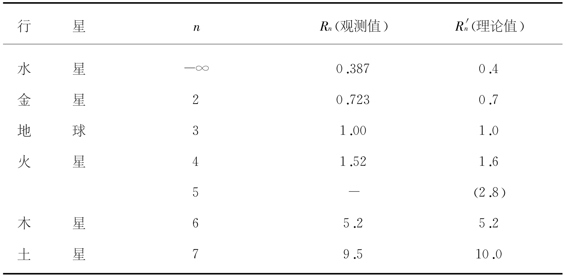
这便是著名的提丢斯-波德定律。

运用不完全归纳法进行推理，由于它的结论所断定的范围超出了前提所提供的信息范围，结论的知识往往揭示出存在于无数现象中的普遍规律，向人们提供了崭新的知识。它能揭示事物的共性，使科学不仅具有描述的功能，还具有预见的功能。就提丢斯-波德定律来说，按照这一经验定律，在火星与木星轨道之间距太阳2.8天文单位处应有一颗行星存在。1801年元旦之夜，意大利西西里岛巴勒莫天文台台长G·皮阿齐果然在这个距离上发现了这颗新天体，后命名为谷神星。因为它质量很小，不能与大行星为伍，故称为小行星。这一发现，显示了由不完全归纳法获得的经验定律对观测实践具有的不可忽视的作用，说明了不完全归纳法比完全归纳法具有较大的创造性。

但是，不完全归纳法是一种可靠性程度较小的方法。因为其前提是单称命题，而结论是特称命题或全称命题，从单称到全称、从已知到未知，不具有逻辑必然性。不完全归纳论证，即使它的所有前提都为真，它的结论的真实性，最多不过是概率比较高，肯定不具有绝对的确定性。全称性归纳是不允许反例存在的，只要出现一个反例，归纳的结论即被推翻。例如，“凡天鹅皆白”，这是人从许许多多天鹅中归纳出来的人所共知的结论，后来却在澳大利亚发现了一只黑天鹅。可见，“以最简单的归纳方法获得的最简单的真理，总是不完全的，因为经验总是未完成的”⁽²⁸⁾。

（2）统计性归纳法

即是以概率命题的形式表述其归纳成果的一种方法。它是发现大量随机事件的概率统计定律的主要手段。凡是统计性规律都是以概率命题来陈述。统计性归纳法也有完全归纳法和不完全归纳法之分。但大多数的统计概括是应用不完全归纳法的或然性概括，即抽取一部分个体作为样本，由对样本的考察概括出总体的概率统计特性。应用统计性归纳法进行统计概括，其逻辑模式为：“样本中百分之几的S是P；所以，总体中的百分之几的S是P。”

例如，19世纪中叶G·J·孟德尔的遗传分离定律（“75%的子二代植株表现为显性的性状”）就是由统计性归纳法得出的。自1857年到1865年，G·J·孟德尔用八年时间进行豌豆杂交实验，他集中观察记录了豌豆七个相对性状的遗传现象。这七个相对性状分别是：种子形状（圆形与皱形）、子叶颜色（黄色与绿色）、花的颜色（红色与白色）、成熟荚形（饱满与不饱满）、未成熟豆荚颜色（绿色与黄色）、花着生位置（腋生与顶生）、蔓茎高度（高茎与矮茎）。G·J·孟德尔将前者，即种子圆形、子叶黄色、花朵红色、豆荚饱满、豆荚绿色、花腋生、高茎称为显性性状；将后者，即种子皱形、子叶绿色、花朵白色、豆荚不饱满、豆荚黄色、花顶生、矮茎称为隐性性状。当G·J·孟德尔把具有任一相对性状的甲、乙两个品种进行正、反杂交时，它们的子一代都表现出显性性状。子一代自交所得的子二代，有的表现为显性性状，有的表现为隐性性状，具体记录如表7-2所示。G·J·孟德尔由这些试验数据进行统计概括，便发现了遗传学上的分离定律。他认为，生物学的每一相对性状都由一对相对“因子”决定，相对性状有显性性状与隐性性状之分，显性性状包含着显现因子，隐性性状包含着隐性因子，杂交所得的子一代都呈显性性状，再杂交所得的子二代，其显性性状与隐性性状即以3与1之比⁽²⁹⁾分离。

显然，统计性归纳法是一个或然性概括的逻辑模式，前提真时结论不一定真。如何才能提高这种统计概括的或然性程度呢？关键在于抽样，也就是要使抽取的样本是个优样。一个优样要满足下述两个要求：一是代表性。就是要使样本的概率统计特性能代表总体的概率统计特性。从量上说，样本中的个体要达到一定的数量，即样本要达到一定的容量。统计概括所研究的是随机现象的概率统计规律，反映这种概率统计规律性的概率统计定律只有在相同条件下进行大量重复试验或观察中才显现出来。从质上说，样本中各个个体之间的差异必须和总体中各个个体之间的差异相一致。为了做到这一点，经常采取分层抽样和加权统计平均数的办法。二是独立性。就是从总体中抽取子样必须是随机的，即每个个体都有同等概率被抽取。不能在抽样时只抽取有利于自己的猜测或设想的一些个体，对不利于自己的猜测或设想的个体视而不见。

表7-2　由子一代自交所得的子二代性状

2.演绎方法

演绎方法是从一般到个别的认识方法。它从一般性的原理出发，对个别的或特殊的事物进行分析、推理，从而达到相应的结论。三段论是演绎方法的主要形式，它由大前提、小前提和结论三部分构成。大前提是已知的一般原理或假说，小前提是所研究的个别事实的判断。前提和结论之间有必然的蕴涵关系。例如：

演绎方法在逻辑学中称为演绎推理。演绎推理的结论通常是隐含的，已经包含在它的前提之中。这就是说，演绎推理的基本特点是前提与结论之间的联系具有蕴涵关系，或者说前提与结论之间具有必然联系。在演绎推理中，从真实的前提出发，遵从形式逻辑关于推理形式的规则，就必然得出真实的结论。亦即一个有效的演绎论证，只要它的前提都为真，它的结论必然为真，并具有可靠的确定性。

虽然演绎推理规则固定，推理结论总跳不出前提所设定的知识范围，但是在理论层次的科学认识中，演绎推理有着特殊重要的意义。因为演绎推理是一种必然性推理，只要合乎逻辑，从真实的前提出发，通过演绎就能推出真实的结论。由于演绎的这个根本特征，在建立严密的理论体系时，往往应用演绎推理作为科学解释的基础。它不仅通过基本概念的推演，使某个领域的知识不再是零散的、孤立的，而且一个命题的真实性也可以在相关的体系中通过演绎推理予以证明和反驳。这种逻辑证明虽然是间接的，不能作为客观真理性的标准，但却是实践证明的不可缺少的手段。有些命题本身很难或者根本不可能用实践直接检验，往往是靠检验命题的逻辑推论得到证明和反驳。这个作用在一切用公理构造起来的理论体系中，表现得非常突出。整个欧几里得几何学就是一个演绎推理的体系，经典力学以及相对论、量子力学也基本上是靠演绎推理建立起来的理论体系。演绎推理还是用以做出科学预见的重要手段。演绎方法所揭示的前提中蕴涵的内容有可能涉及还没有被人们考察的领域，那就有可能发现未知。例如，中微子的发现，就离不开演绎方法的妙用。物理学家W·E·泡利在研究原子核的β衰变时，发现衰变放射出来的电子带走的能量小于原子核亏损的能量。他根据能量守恒的原理做出演绎推论，预言了在β衰变中可能还存在一种尚未被发现的中性微小粒子，是它带走了一部分能量。后来费米把它命名为“中微子”。1956年和1968年，人们终于间接和直接找到了中微子，确证了W·E·泡利的科学预见。

归纳方法和演绎方法，都是科学发现的重要手段，所不同的主要在于前者多用于经验层次，后者多用于理论层次；前者是或然性推理，后者是必然性推理。忽视这个差别，看不到它们在科学发现中的不同作用，显然不利于自觉地把科学认识从经验层次上升为理论层次。然而，从现代科学认识论来看，归纳与演绎是辩证统一的，其中任何一方都不能成为科学发现的惟一形式。认识的经验层次和理论层次只不过是科学认识的不同环节，在整个人类认识的历史长河中，它们又是一环套一环的，其中任何一个环节都不能脱离其他环节而孤立存在。归纳和演绎也一样，它们相互联系、相互渗透、相互依存，已经积累的知识总是要在每一次归纳中起指导作用，完全脱离已知原理的指导，归纳是盲目的、毫无科学价值；反之，归纳是演绎的基础，演绎的出发点和前提是由归纳得来的，演绎推理没有归纳得来的一般原理也是不可想象的。

3.类比方法

所谓类比方法，是根据两个或两类对象之间某些方面的相似或相同，而推出它们在其他方面也可能相似或相同的一种逻辑思维方法。通过对两个或两类不同的对象进行比较，找出它们的相似点或相同点，然后以此为根据，把其中某一对象的有关知识推移到另一对象中去，这一过程就是运用类比方法进行推理的过程，即类比推理。可表示为

若　A∈P ₁，P₂，…，P_n，P_n＋1，

则

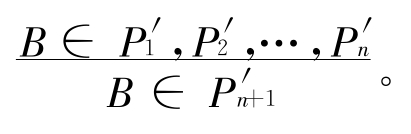
类比方法既不同于归纳方法的从个别推到一般，也不同于演绎方法的从一般推到个别，它的推理可以是“特殊—特殊”，也可以是“一般—一般”。虽然归纳、演绎和类比这三种推理方法都是从已知的前提推出结论，结论皆在不同程度上受到前提的制约，但是结论受到前提制约的程度是不同的。其中，演绎推理的结果受到前提的限制最大，归纳推理的结论受到前提的限制次之，而类比推理的结论受到前提的限制最小，这就使得类比方法在科学探索中具有很大的创造性。类比推理的客观基础是事物之间存在普遍联系的本性。由于对象之间不仅具有相似性，而且具有差异性，类比方法舍弃了推理过程中的未知的中间环节和因素，其结论具有很大的或然性。

类比推理的思维过程，其基本环节是联想和比较。首先是选取何种类比对象的联想和比较，其次是对所研究的对象在形态、属性、结构、功能方面以及理论的原则、形式、方法、内容方面的联想和比较，以便从对已知对象的判断过渡到对未知对象的判断。

类比方法为人们的思维过程提供了广阔的“自由创造”的天地，使它成为科学研究中富有创造性的思维方式。日本著名科学家汤川秀树说：“类比是一种创造性思维的形式……假定存在一个人所不能理解的某物，他偶尔注意到这一某物与他所熟悉的某一他物的相似性。他通过将两者比较就可以理解他在此刻之前尚不能理解的某物。如果他的理解是恰当的而且还没有人达到这样的理解，那么他就可以说他的思维确实是创造性的。”⁽³⁰⁾N·维纳等人将机器与生物类比，找到了两者的相似性，从而创立了控制论。在N·维纳看来，“把生命机体和机器作类比工作，可能是当代最伟大的贡献”⁽³¹⁾。

根据类比物已知属性之间关系的不同，可以将类比方法分为简单共存类比、因果类比、对称类比、协变类比等几种不同的类型。

（1）简单共存类比(www.xing528.com)

是根据对象的属性之间具有简单共存关系而进行的推理。即在对象A中P₁，P₂，…，P_n与P_n＋1有共存关系，对象B中也有，所以对象B可能有与其他属性共存。例如，曾有一位业余地震研究者在某次地震之前观察到天空出现奇特的云彩，并记录了这次地震的时间、方位和裂度。后来，他又看到了这种云彩，就推测又将发生地震，并预言了地震的大致时间、方位和裂度，果然言中。但这种类比很肤浅，其可靠程度较低。

（2）因果类比

是根据对象的属性之间具有因果关系而进行的推理。即在对象A中，P ₁，P₂，…，P_n与P_n＋1有因果关系，对象B中有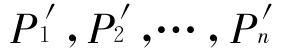，所以对象B可能有果。例如，19世纪英国物理学家T·杨将光与声进行类比，得到了光是一种波的见解。因为声音有直线传播、反射和折射等现象，尤其是它有干涉现象，其原因就在于它的波动性；光在这种因果关系中也有直线传播、反射和折射现象，尤其它也有干涉现象，所以光可能具有波动性。在这种类比中，由于对象的各种属性不再是简单共存关系，而是有了某种因果的必然联系，因而提高了结论的可靠性。但由于一种原因可产生不同的结果，或同一结果也可能由不同原因造成，所以也还不能保证这种推理的结论一定正确。

（3）对称类比

是根据对象的属性之间具有对称性而进行的推理。即对象A中P₁与P₂有对称关系，对象B在这种对称关系中有，所以对象B中可能有与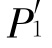相对称。例如，1930年著名物理学家P·A·M·狄拉克把相对论原理引进量子力学，建立了描述自由电子运动的方程，在解这个方程时，得到了正负对称的两种能量解。正的能量对应着电子，那么负的能量对应着什么呢？已知电荷有正电荷和负电荷的对称性，既然有带负电的电子，那么是否也有带正电的电子呢？为了解释上述方程的解，P·A·M·狄拉克运用了对称类比法，认为对应负的能量的粒子可能是带正电荷的电子。1932年，美国物理学家C·D·安德森在宇宙射线的实验中果然发现了正电子。

（4）协变类比

是根据两个对象的属性之间具有某种定量的比例变化、函数变化关系即确定的协变关系所进行的推理。这种类比方法定量地描述了对象的属性之间的关系，比前面几种只作定性描述的类比方法前进了一步，使对象属性之间的关系更为确定，因而具有更高的可靠性。

例如，1923年法国物理学家P·L·V·德布罗意用协变类比提出了物质波的假说。他把光学现象与力学现象作了如下的比较。

在几何光学中，光波的运动服从最短程原理即费尔马原理，其数学形式为

其中dS为光线路程元，v为光速，而这一最短程原理可以从波动理论中导出。

在经典力学中，质点的运动服从最小作用量原理即哈密顿原理，其数学形式为

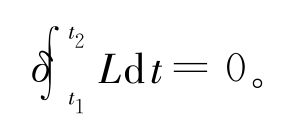
其中L为拉格朗日函数，dt为时间元。

可见，这两个反映不同领域运动规律的原理具有相似的数学形式。又知光不但具有波动性，而且具有粒子性。P·L·V·德布罗意由此推出物质粒子也具有波动性，即著名的物质波假说。这一假说在1927年为C·J·戴维逊和L·H·革末的电子单晶衍射实验所确证。

类比方法的推理过程，其实还有一潜在的中介物，即假定有把类比对象统一起来的大系统或它的普遍规律。于是思维从已知的特殊上升为假定的“一般”，再由这个“一般”演绎为未知的特殊。如物质波假说的例子就是：波的粒子性（特殊理论）任何物质具有波粒二象性（一般理论）粒子的波动性（特殊理论）。

不过，这个中介物在类比过程中不需要明白显示，也不必先作出证明，因此仍表现为“特殊—特殊”、“一般—一般”的直达过程。从这里可以看出，归纳、演绎、类比之间有着内在的联系，类比本质上是归纳和演绎的辩证综合。

4.思想实验

思想实验（thought‐experiment），又称思维实验、假想实验或抽象实验。这是一种在高度理想化的条件下，在科学想象之中进行的特殊的“实验”。科学探索的直接对象在很多情况下都是理想化客体，例如质点、刚体、理想气体、点电荷、绝对黑体等。同样的道理，在思想实验中，假想实验者使用理想化的仪器设备（如G·伽利略的绝对光滑的斜面、平面与悬线重量忽略不计的理想摆，A·爱因斯坦的理想列车与理想升降机等），在极端理想化的条件下（如无摩擦、无空气阻力，或者完全摆脱引力影响处在“自由空间”之中等）对实验对象（各种理想客体）进行“操作”和“观察”。这是思想的操作和观察，是用“思想的手”和“理性的眼睛”所进行的操作和观察，只有凭借推理和想象才能“看到”理想客体的纯态表现。例如，在实际的实验中，人们看到道路越平滑，车子向前冲得越远；而在思想实验中，则将会发现车子在无摩擦的道路上永远运动下去。众所周知，这就是G·伽利略所做的一个思想实验，他通过这个实验提出了著名的惯性定律。A·爱因斯坦曾指出：“惯性定律标志着物理学上第一个大进步，事实上是物理学的真正开端。它是由考虑一个既没有摩擦又没有任何外力作用而永远运动的物体的思想实验而得来的。从这个例子以及后来的许多旁的例子中，我们认识到用思维来创造思想实验的重要性。”⁽³²⁾

在科学史上，一些重要原理的发现，不少重大的理论突破，确实都同科学家运用思想实验有关。就A·爱因斯坦本人来说，他所确立的相对论的一些重要观念，几乎都借助于思想实验。他在16岁时就已经得到了：如果他以光速追踪一条光线运动，是否看到光线是静止在空间振荡着的电磁波。他认为，这是与他创立狭义相对论有关的“第一个朴素的思想实验”——追踪光的思想实验。这一思想实验启发他认识到存在于经典力学基础同麦克斯韦电磁理论之间的矛盾。因为依据经典力学的伽利略变换（力学相对性原理），观察者以光速追踪光，他就“应当看到，这样一条光线就好像一个在空间里振荡着而停滞不前的电磁场”⁽³³⁾。可是，无论是依据经验，还是按照麦克斯韦方程，看来都不会有这样的事情。亦即依据光行差效应测得的光速，按照A·H·L·斐索、J·B·L·傅科设计的实验测得的光速都是相同的，光的传播速度与光源、介质及接受装置的运动无关，从麦克斯韦电磁理论的波动方程导出的光速也是一个恒定的常数。可是伽利略变换也是有大量经验事实为依据的。为什么在以光速追踪光的思想实验中，伽利略变换同J·C·麦克斯韦的波动方程绝对不相容呢？经过10年沉思，A·爱因斯坦找到了产生这一悖论的根源，即是隐含在伽利略变换中的“绝对时间”观念。

之后，A·爱因斯坦又巧妙地设计了“火车”的思想实验，通过这一思想实验的分析得到同时性的相对性原理。他设想，当两道闪电同时下击一条东西走向的铁路轨道时，对于站在两道闪电中点铁路旁的观察者来说，两道闪电是同时发生的，而对于乘坐一列由西向东高速行进并正好经过两道闪电中点的观察者来说，则先看到东边的闪电而后才看到西边的闪电。若火车以光速前进的话，则只能看到东边的闪电，永远看不到西边的闪电（图7-4）。A·爱因斯坦由此得出：“我们不能给予同时性这概念以任何绝对的意义，两个事件，从一个坐标系看来是同时的，而从另一个相对于这个坐标系运动着的坐标系看来，它们就不能再被认为是同时的事件了。”⁽³⁴⁾这就是所谓同时性的相对性原理。

图7-4　思想火车引出同时性的相对性原理

A·爱因斯坦关于加速系统和引力场进行比较的思想实验，则对广义相对论的创立起了重要作用。他设想一个远离一切天体的无引力作用的封闭大箱子，当箱子静止时箱内的观察者是处在一个惯性系中；而当箱子向上作匀加速运动，箱内的观察者会以为自己是处在一个作用方向指向箱底的引力场中。也就是说，“在一个封闭箱中的观察者，不管用什么方法也不能确定，究竟箱是静止在一个静止的引力场中呢，还是处在没有引力场但却作加速运动（由加于箱的力所引起）的空间中呢”⁽³⁵⁾？这个思想实验使得A·爱因斯坦于1907年提出了“引力场同参照系的相当的加速度在物理上完全等价”的等效原理（图7-5）。

图7-5　思想升降机引出等效原理

图7-6　思想升降机中的光线弯曲

1911年，A·爱因斯坦依据等效原理讨论了“引力对光传播的影响”。他又是从一个思想实验的分析中引出结论的。还是上面假想的那个远离一切引力作用的封闭箱子，从左壁射进一束光，箱子静止，箱内的观察者会发现光是沿直线传播射到右壁；而当箱子向上作加速运动，那么观察者就在相对于从左壁射出的光的竖直方向上运动，因此会发现光线向下弯曲（图7-6）。根据加速系统同引力场等效，也就是说光在引力场中传播会发生弯曲。这个思想实验不仅帮助A·爱因斯坦考察了引力场的性质，而且还导出了能为天文观测检验的效应。A·爱因斯坦计算出了光线经过太阳表面弯曲的弧度。1919年，英国天文学家A·S·爱丁顿对日全食的观测证实了A·爱因斯坦的这一预言。

由上述的实例分析，可知思想实验并不是实际进行的实验，而是一种借助于形象思维以逻辑思维为主的思维活动，这种思维活动按照实验的格式展开，所以也称“实验”。但是，它与通常的实验相比，又具有下述独特的基本特征。

（1）思想性

即思想实验是借助于表象（形象思维）和逻辑思维来进行的。思想实验中的观察者、实验对象、仪器装置、实验的操作过程，并不是真实的性质和物质过程，而只是由以往的经验所表象出来的一些形象观念。在思想实验中，既没有实在的仪器设备，又没有实在的实验对象，更没有实际的实验操作，这些都是由思想以抽象的形式提供的。正因为如此，有一种看法认为，思想实验是一种形象思维和逻辑思维有机结合的科学认识方法⁽³⁶⁾。

（2）超现实性

即思想实验是当时的现实实验所无法实现的实验，是超越现实条件的实验。实际的实验受到具体的条件的限制，使得许多自然事物很难或根本不可能成为实验对象，人们难以或根本无法身临其境地进行操作、观察。而思想实验可以不受任何限制地对任意对象进行实验。思想可以“自由翱翔”，借助于想象能够把实验者置身于任何对象的环境之中。当然，并非所有思想实验的对象都不能进入实验室的。有的思想实验在一定历史时期可能是不能实现的，但是随着科学技术和物质生产的发展，则可以把那时不能实现的思想实验实现出来。有些思想实验在一定条件下可以转变为真实的实验。如A·爱因斯坦在思考为建立广义相对论而提出的“等效原理”所设计的思想实验，在如今，已由宇航员在宇宙飞船或航天飞机上得到了验证。当然，也确有一些思想实验是永远不可能得到最后证明，惯性实验就是如此。人们不可能使球体沿水平面无摩擦地永远等速直线运动下去，虽然人类不断设法使接触面的摩擦系数趋近于零。

（3）待检性

即由思想实验得到的结果还需要实际实验、观测的检验。只有经过实际实验、观测的验证，它才具有经验事实的内容和价值。例如，A·爱因斯坦从思想实验中得到的光线通过引力场弯曲的结论，只是在通过了1919年A·S·爱丁顿等人的日食观测检验后才变成真正的科学事实。