自然演化的基本方式：当代科学技术哲学导论

三、自然演化的基本方式

从前面阐述的生命的起源和演化可以看出，生物进化是一种从简单的、单一的状态向着复杂的、多种可能状态的树状的分化过程。实际上，这种“进化树”模式是自然演化的一种普遍的基本方式。

1.分岔：稳定性与不稳定性

（1）自然系统演化的分岔现象

现代非平衡态热力理论和混沌理论的研究表明，分岔（bifurcations）是现实世界中复杂系统的一种奇特的和基本的行为方式。“分岔是系统各部分与系统及其环境之间的内禀差别的表现。”⁽⁵⁶⁾进化是开放系统在远离平衡态的条件下，按照突现分岔、多束轨线的方式进行的。如果说，自然系统开始于一个或同一的原始状态，那么在以后的演化中，就会由随机涨落而不断发生分岔，出现多种方向、多种形态。分岔确实可以被视为多样化和创新之源，如I·普里戈金所说：“我们的宇宙遵循一条包含逐次分岔的路径……值得庆幸的是，我们遵循的这条路径产生了生命、文化和艺术。”⁽⁵⁷⁾自然系统演化的分岔现象均可用图2-1表示，其中μ表示状态参量，μc表示临界值（upper‐thresholds）。X是μ的函数，表征离开平衡态的距离。在分岔点，热力学分支失稳，出现了两个新解b₁和b₂。这种在各种不同现象中出现同样性质的结构的状况，包含着含义深刻的统一性。它表明非线性非平衡系统发生相变时，面临着多种可能的前途，存在着多种可能的选择，即系统的发展演化出现了分岔。

图2-1　分岔示意图

作为一个比喻，我们设想一个小球在路面上运动，前方被一个小丘隔开（即被分岔），小球不得不通向被小丘分开的两条路径（如图2-1中分支b1和b2）中的一条。从这一设想进一步想象开去，倘若回到远古时代，将小球换成恐龙，或是人类的原始祖先，它们也同样面临着分岔。在间断平衡的进化理论中，有一个被赋予重要地位且经常运用的概念——“隔离”，隔离起着在分岔后稳定物种发展的作用。地理隔离而后导致生殖隔离，于是物种的突变便稳定成新的种，即新物种形成。

分岔的选择或二中择一，表现在通过远离平衡态对外部随机涨落的敏感上。没有远离平衡，微小的涨落随生随灭，对系统并不造成大的影响；远离平衡时，系统对微小涨落变得极为敏感。在这种情形下，一个小的扰动就足以使得系统从热力学分支进入耗散结构分支。随着条件的改变，系统还可能出现新的临界点，出现新的分岔即二级分岔，再往后又可能出现更高级的分岔。这种现象被称作逐级分岔。逐级分叉使得系统从一种有序进入更高一级的有序，从而为自然系统的演化提供了一定的说明。

（2）稳定性与不稳定性的统一

分岔表明了稳定性与不稳定性的辩证的对立统一。对系统进化而言，稳定性是不稳定性的基础，而不稳定性则是到达新的稳定性的必经之路。当自然系统在一种稳定状态难以挽回地被扰乱，即不稳定性达到一定的临界阈值时，就会发生突变分岔，而一旦分岔发生，选择作用过后，系统进入新态，新的稳定性又开始起支配作用。系统的演化作为逐级分岔的层次跃迁的过程，就是经过一系列的稳定——失稳——稳定状态，按较突然的跃迁、爆发的方式越过稳定阈外而进行的。分岔造成了多重稳定状态：当一种平衡状态难以挽回地被扰乱和推开后，便有另外的稳定状态可供选择。在这一进化的历史中，离热力学平衡态越远的系统，用以维持动态平衡的那些反馈和催化循环就越复杂、越高级，对改变自己的结构就越敏感。于是远离平衡的系统越趋复杂，而越趋复杂的系统就越能够在许多不同的平稳状态下存在，并且可供采取的平稳状态也随着系统的复杂性和不稳定程度成比例地增长（图2-2）⁽⁵⁸⁾。无论是非生命界还是生命界、人类社会，这种进化图景都是普遍适用的。

分岔是对称破缺之源。从基本粒子到社会系统的生成，之所以形成一层一层稳定的层次结构，就是演化的分岔造成现存的存在层次。

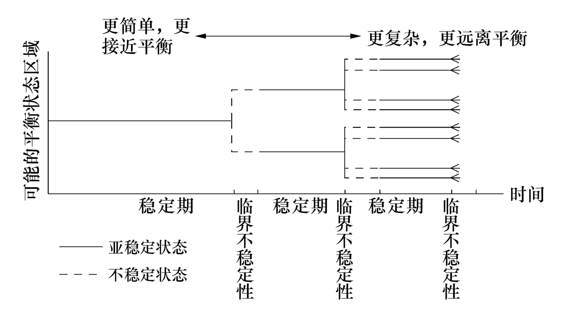
图2-2　分岔：在非平衡的更高层次上替换状态增加

2.突现：突发性、间断性、不可还原性和不可预测性

（1）“突现”的概念

“突现”一词的英文“emergence”，来源于拉丁语“emerge”，其本意是“从液体中浮出”（come upout of liquid），引申为“现出、显现”（come into view）、“生成、露出”（issue）等。然而，“emergence”一词的后缀“ence”的拉丁语是表示状态的。所以，理解突现不仅要注意到其突发性的一面，而且更重要的是理解突发后显现的状态⁽⁵⁹⁾。

突现作为一个学术术语的提出，可以追溯到近代J·S·穆勒的两种因果关系学说。J·S·穆勒认为，存在的两种因果关系，一种是“合成因果关系”，即由同质的原因（homeopathic causes）以合力的原则导致其结果，这个结果等于诸种同质原因分别作用的总和（例如力的合成），这种因果关系由同质定律所支配；另一种因果关系称为“异质效应”（heteropathic effect），其特征是多个原因共同作用产生的结果，不等于各个原因单独作用的总和，这种因果关系由异质定律所支配（例如氢氧化合成水，水就不是氢、氧分别作用的总和）。

1875年，哲学家L·H·刘易斯继承了J·S·穆勒的思想，将第二种因果关系称为“突现”，由此赋予突现以哲学意义。

值得一提的是，美国生物学家T·H·摩尔根在1923年出版的《突现的演化》一书中，明确提出：“宇宙在进行的每一阶段上都有新的性质，新的事物突然地、神秘地被创造出来。”⁽⁶⁰⁾

下述学者对“突现”所作的阐释，表明“突现”概念与系统的整体性之间是有密切联系的。

W·R·艾什比在1956年出版的《控制论导论》一书中写道：“突现这一概念从来没有人明确下过定义，但以下例子也许可以作为讨论的基础：（a）氨是气体，氯化氢也是气体。这两种气体混合在一起，结果得到固体——这是两种反应物原来都没有的性质。（b）碳、氢、氧几乎都是无味的，但它们的一种特定化合物糖却具有一种甜味，是三者都没有的。（c）细菌体内20种左右的氨基酸都没有繁殖的性质，但它们合在一起（再加上一些别的物质）之后，却具有这种性质。”其意思是说，突现是指系统具有它的部分所没有的性质。

M·邦格从系统的组成对突现概念作了如下定义：“设X为一具有A组成C_A （X）的系统，P为X的属性，则有：（a）P是A的组合（resultant）（或相对于层次A的组合），当且仅当X的每一A分量（component）都具有P。（b）不然的话，即如果X的任一A都不具有P，则P是A的突现（或相对于层次A的突现）。”他举例说：“一个细胞的成分是不具有生命的，因此相对于细胞成分而言，生命就是突现的而不是组合的。另外，感觉、感情和思想是多细胞神经系统的功能，个别神经系统是不可能具有的，因此，它们也是突现的。”⁽⁶¹⁾

J·L·卡斯蒂在1996年出版的《虚实世界》一书中指出：“突现是作为总体系统行为从多个参与者的相互作用中所产生出的‘系统论’的泛称，是一种从系统的各个组成部分的孤立行为中无法预测，甚至无法想象的行为。”⁽⁶²⁾

还有学者提出：“突现是指在复杂系统的自组织过程中出现的新颖的和连贯的结构、模式和性质，相对于它们所出自的微观层次的组成部分和过程，突现现象是在宏观层次上出现的现象。”⁽⁶³⁾

由此可见，所谓突现，是指由系统中的各个组成部分相互作用所产生的新的形态、结构和性质。对自然系统的演化而言，即是指自然系统的新的形态、结构和性质作为整体的突然出现。

（2）自然系统的突现的基本特点

突现是一个演化论的概念，它表征系统的整体性从潜在的有到实在的有的创生过程。自然系统的演化过程的展开，本质上即是系统新质逐级突现的结果。

从数学上的突变论、自组织的分岔理论以及实际过程来看，自然系统的突现具有突发性、间断性、不可还原性和不可预测性等典型特征。

突现的突发性特点是很明显的，正如L·V·贝塔朗菲所指出的：“构成特征不能由孤立的各部分的特征来说明。因此复合体的特征与元素特征相比是‘新的’或‘突然发生的’。”“虽然我们可以设想某个总和是逐渐形成的，但作为具有相互关系的部分的总体的系统必须设想为瞬间形成的。”⁽⁶⁴⁾

所谓间断性，则是指系统跃入新的状态所具有的一种非连续的变化，它既是渐进过程的中断，又是稳定过程的中断。就生物进化而言，对于进化的间断性，过去在C·R·达尔文的理论中是不被承认的，C·R·达尔文说过：“自然选择仅能借着轻微的、连续的、有利的变异之累积而发生作用，所以它不能产生巨大的或突然的变化；它只能按照短小的和缓慢的步骤而发生作用。”他信奉C·V·林耐的箴言：“自然界中没有飞跃。”⁽⁶⁵⁾可是大自然无视19世纪这位英国人的意向和安排，照常按照突然性的飞跃这种方式前进。1972年，差不多在《物种起源》出版120年之后，哈佛大学的S·J·古尔德和美国自然博物馆的N·埃尔德里奇发表了《间断平衡：代替种系发生渐进主义》，以他们创立的“间断平衡论”（punctuated equilibria），把飞跃引入了新达尔文主义生物学。他们强调生物的进化是渐变与突变、连续与间断的统一。认为进化的稳定状态总是由一批分享相似生态序的物种同环境的动态平衡造成的，其中有一个占支配地位的种群和占支配地位的循环圈。进化之所以发生，是由于有其他物种或亚种偶然闯进了边缘并打破了占支配地位的循环圈，从而使在进化分支中占支配地位的种群在自己的环境中失稳了。于是，长时期的静态稳定被破坏，出现了从原先占支配地位而受到灭绝威胁的种群向处在边缘的物种或亚种的进化性飞跃。这个过程是比较突然的，新物种的出现使已有物种基本保持不变的一个很长的时期中断了。“间断平衡论”肯定了突然发生的不稳定性与突然发生的相变在物种形成中的重要作用。按照这一理论，生命进化树状分岔图不再像过去绘制出来的那样由连续的“Y”字形连接而成的样子，而是用笔直的折线画成，从原先占支配地位的物种拐向原先一直在边缘而现在取得了支配地位的物种⁽⁶⁶⁾（图2-3）。

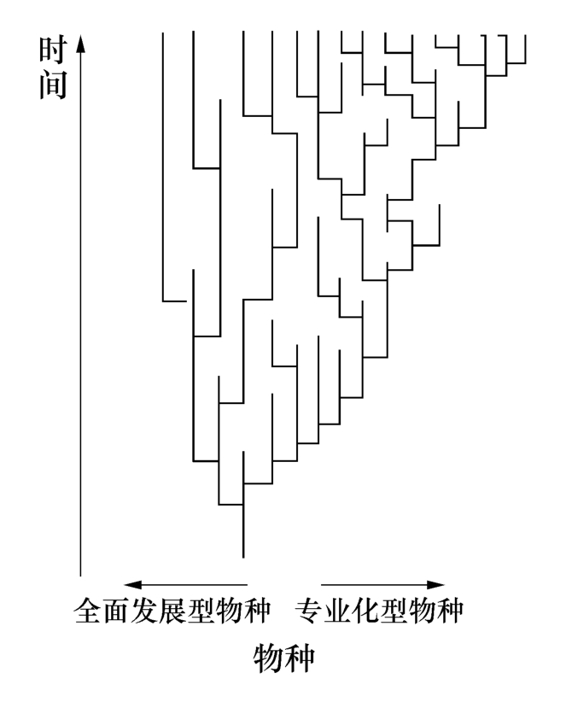
图2-3　生物进化过程中新物种的形成

突现表现为系统层次间具有不可还原性。每一个层次都具有某些基本的、不可还原的性质和规律，高层级性质是从低层级性质中突现出来的。系统的一个性质被认为是突现的，当且仅当它是不仅拥有低层次组分及其行为所不具有的性质和行为，而且高层次的性质和行为不能通过还原得到解释，亦即包括在本体论和认识论上的不可还原。

本体的不可还原性，是因为系统宏观层次具有“下向因果关系”（downward causation）而具有的不可还原性。“所谓下向因果关系原理就是处于层级的低层次的所有过程受到高层次规律的约束，并遵照这些规律行事。”⁽⁶⁷⁾即系统宏观层次对其微观层次的组成部分施加的一种下行的因果效应。认识的不可还原性是指整体性质的不可分析性。不管是从微观上还是从宏观上，那些在行为上不可分析的系统整体属性，就是不可还原的。

由于突现具有宏观层次的独特行为和规律，因此，对突现的解释就需要对宏观层次的行为规律进行描述和刻画。还原论正是试图消解宏观层次的规律，完全用低层次规律来解释和代替宏观层次规律。复杂系统突现论则认为，突现的解释在认识论上不仅是必需的而且是自主的，为不可被还原解释所代替。

突现性还表现为进化过程中新事物或性质生成的不可预测性。自然系统的进化包含着前后相继的各种运动过程，其中一个重要方面，即是临界点上新质的突然产生。分岔理论表明，在临界点上，系统可能进入多种状态，从逻辑上讲，这些状态形成的机会是均等的，而现实的突现状态只是多种可能性的一种。因此，人们只能对此作出概率性的预测，这就是突现的不可预测性特点。也就是说，在突现出现之前，即使人们对支配它的组成部分的特征及其规律有所认识，也不能预言它的出现。关于不可预测性的发生，我们将在下面作进一步讨论。

3.确定性与随机性：混沌理论和“内在随机性”

（1）混沌理论与“混沌”概念

混沌理论被认为是非线性科学中最前沿的分支。从20世纪初叶开始，一批才华横溢、思想深邃的科学家相继为混沌理论的建立作出了重要贡献。

1908年法国著名数学家H·庞加莱在其出版的《科学与方法》中就指出：“如果我们能够精确地了解自然定律以及宇宙在初始时刻的状态，那么我们就能够正确地预言宇宙在后继时刻的状态。不过，即使自然定律对我们已无进一步的秘密可言，我们也只能近似地知道初始状态。”他说：“可以发生这样的情况：初始条件的微小差别在最后的现象中产生了极大的差别；前者的微小误差造成了后者的巨大误差。于是，预言变得不可能了。”⁽⁶⁸⁾

1961年，美国气象学家E·洛伦兹在研究天气预报时发现，两条相似的天气曲线，尽管它们的初始值相差不过千分之一，然而，曲线却因此而迅速偏离，一开始还有些相似性，但是不到两个月，相似性已彻底消失，变成两条完全不同的曲线。1963年，E·洛伦兹发表《确定性的非周期流》一文，第一次明确地从确定性方程得到随机性的结果。E·洛伦兹的数值天气预报的方程是确定的、非线性的，但通过计算机数值计算时，发现当初始值出现微小误差时，方程的解却出现非周期振荡（随机性）。随后，M·埃侬、O·若斯勒等人得到类似结果。

1975年，美国马里兰大学李天岩和J·约克在《数学月刊》上发表题为“周期3意味着混沌”（Period Three Implies Chaos）一文，这是最早的“混沌”的数学定义。

粗略地看，非线性动力学混沌好像是突然涌现于当代科学界的。但是，考察一下历史，就会找到一种奇妙的、几乎连续的混沌思想发展脉络。

“混沌”（chaos，亦作“浑沌”）这个词源远流长。公元前8世纪，古希腊神话诗人赫西奥德在他的《神谱》中最先提出混沌（）的概念：“万物之前有混沌，然后才产生宽广的大地。”公元前6世纪，中国古代就有关于盘古开天辟地始于“混沌”或“浑沌”的神话传说。《庄子·应帝王》言东海之帝鲦与北海之帝忽，为了报答中央之帝浑沌，为他开凿耳、目、口、鼻七窍。“日凿一窍，七日浑沌死”。庄子借此说明中央之帝塑造出来的面目未分、浑然一体的浑沌，是一种自然状态，它的存在是有条件的，因而是可以消除的，即一旦开了窍，其内在的差异表现出来，浑沌便不复存在了。

在世界文化典籍中，“混沌”一词有着丰富的内涵。综合地看，至少有下述三种主要指称。

一是指自然或宇宙的原始状态。除上述的《神谱》和《庄子》的哲学议论外，又如：西汉淮南王刘安编撰的《淮南子·诠言训》：“洞同天地，浑沌为朴，未造而成物，谓之太一。”形成于中国西汉中期的纬书《易纬》：“气似质具而未相离，谓之混沌。”（《易纬·乾凿度》）三国曹植的《七启》：“夫太极之初，浑沌未分。”古罗马诗人P·奥维德的《变形记》：“天地未形，笼罩一切、充塞宇宙者，实为一相，今名之为混沌。”

二是指社会的黑暗状态。例如，西汉司马迁的《史记·五帝本纪》：“昔帝鸿氏有不才子，掩义隐贼，好行凶慝，天下谓之浑沌。”18世纪英国诗人A·蒲柏的《群愚史诗》（1728年）：“瞧！您那可怕的‘混沌’帝国复辟了；光亮在您那寂灭诏令下消失了；伟大的暴君啊！您亲手降下帷幕；无边的黑暗埋葬了一切。”

三是指人们的朦胧茫昧状态。例如：《道德经》第二十章：“我愚人之心也哉！沌沌兮。”《庄子·在宥》：“浑浑沌沌，终身不离。”《张守节正义》：“浑沌，不开通之貌。”

在现代混沌理论中，“混沌”概念有着科学的严格的界定：混沌是确定性系统的“内在随机性”。

（2）混沌：确定性系统内在产生的随机性

我们知道，动力学是研究系统演化即系统状态随时间变化的规律的。这通常可以用微分方程、偏微分方程、差分方程或迭代方程来描述。一旦建立系统的运动方程，系统后一时刻的状态便由前一时刻的状态决定，它们彼此之间的关系是确定的。但是，对于确定性非线性系统，即使没有外部的随机作用，不涉及大数现象或群体效应，初始条件也是确定的，系统自身也会产生出随机性，从而体现了随机性存在于确定性之中，确定性自己规定自己为不确定性。这种不确定性是自然本身所具有的，而并非表明人类的无知。确定性与随机性是密切联系在一起的，正如恩格斯所说：“被判断为必然的东西，是由纯粹的偶然性构成的，而所谓偶然的东西，是一种有必然性隐藏在里面的形式。”⁽⁶⁹⁾

考察最简单的非线性系统——生态学中非常有名的“虫口模型”⁽⁷⁰⁾，即非线性迭代方程：

X_n＋1＝μX _n（1－X_n），

其中，X_n、X_n＋1分别对应于第n代和第n＋1代种群的相对虫口数（状态变量），μ为控制参数，它表示种群的增长率。在物理学上，它意味着对系统施加的驱动，代表非线性的程度。设环境所能容纳的最大虫口数为N₀，第n代虫口数为N _n，则

方程的实际意义要求X在（0，1）内取值，即0≤X≤1；控制参数μ在（0，4）内取值，即0≤μ≤4。

为讨论方便起见，取μ＝4，分别从相差极其微小的三个初始值X₀＝0.1、X₀＝0.100000001、X₀＝0.1000000001开始迭代，通过计算机数值计算，求得X各值，于是有表2-1。

表2-1　X_n＋1＝4X_n（1－X_n）的迭代试验

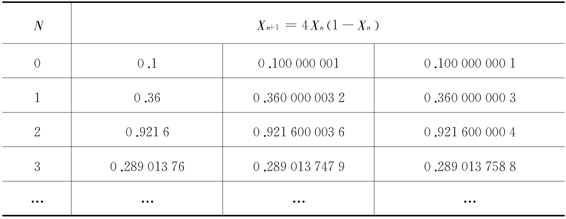
续　表

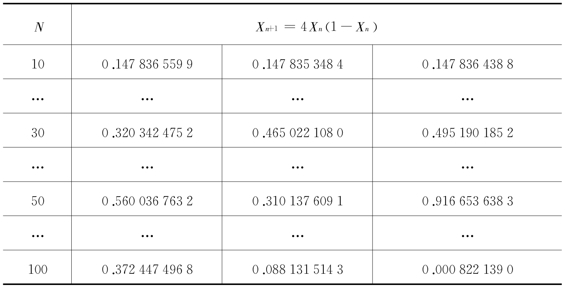
由表2-1可见，当赋给X₀的值稍有不同时，第10次迭代差别还不大，但到第30次迭代时，差别已经较大；到第50次迭代时，差别已经极其显著。这表明具有确定性非线性系统对初始条件的依赖十分敏感，初始值差一点点，后面就可能差很多很多，从而将导致系统长时间行为的不可预测性。这种情况，被E·洛伦兹于1979年在美国科学促进会的一次演讲夸大地说成：“一只蝴蝶在巴西扇动翅膀，会在美国得克萨斯州引来一场风暴。”所谓“蝴蝶效应”，也就是非线性现象具有对初始条件几乎无法预料的灵敏依赖性。

令人惊异的是，早在1906年，法国著名哲学家H·柏格森在其出版的《创造进化论》一书中曾针对机械论和目的论把将来和过去看作是“可以根据现在计算出来的”，认为“一切都是给定的”⁽⁷¹⁾观点，明确指出：“如果一切都能被预见，那么宇宙中就没有任何发明和创造，时间又变得毫无用处。”⁽⁷²⁾并揭示了不可预测性与同不可逆过程相联系的时间之矢的关联。他说：“如果一切都在时间之中，一切都内在地发生变化，那么同样的具体现实事物永远不会重复。”⁽⁷³⁾

不仅如此，一旦系统的非线性程度超过一定的界限，即控制参数μ＞3，系统就会通过倍周期分岔进入混沌⁽⁷⁴⁾。

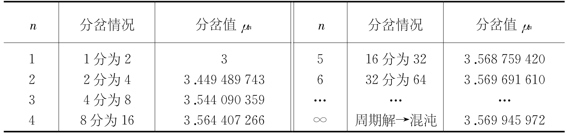
表2-2　f（x）＝μx（1－x）的迭代试验

当0＜μ＜1时，对于0，1之间的任意初值X₀，经过若干次迭代后，系统就会稳定在X_n＝0上，而不再发生变化，意味着虫口系统灭种。在X_n-μ平面（即一维相空间与一维参数空间的乘积空间）上，这类定态点位于参数轴的0到1的线段上（图2-4）。

图2-4　倍周期分岔进入混沌

当1＜μ＜3时，系统仍有一个稳定的迭代结果（若取μ＝2.5，X₀＝0.1，经过若干次迭代后，方程收敛于稳定的解X＝0.6）；随着μ值的增加，X也稍有增加，形成一条从左向右的稍稍上升的曲线。

当3≤μ＜3.449489 743时，系统就有两个稳定的解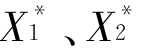，表现为曲线一分为二。若取＝3.159 876 532，则稳定的两周期点为X₁＝0.529 191 619，X₂＝0.787 276 442。继续进行迭代计算，结果将是这两个值交替出现。对于虫口系统，这意味着今年虫口数为X₁，则明年的虫口数为X₂，后年的虫口数又回到X₁，周而复始。

当3.449 489 743≤μ＜3.544 090 359时，系统会有四个稳定的解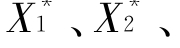，表现为曲线二分为四。若取μ＝3.521 098 765计算，则这个稳定的四周期点为X₁＝0.879 711 981，X₂＝0.372 598 486，X₃＝0.823 123 224，X₄＝0.512 641 636，对于虫口系统，即意味着虫口数以此四点周期变动。

当3.544 090 359≤μ＜3.564 407 266时，系统会有八个稳定的解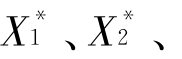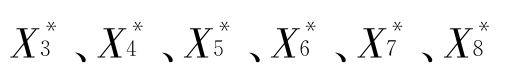，表现为曲线四分为八。若取μ＝3.544 090 359计算，则稳定的八周期点为X₁＝0.523 715 968，X₂＝0.884 029 226，X₃＝0.363 345 649，X₄＝0.819 838 787，X₅＝0.523 473 310，X₆＝0.884 069 809，X₇＝0.363 235 174，X₈＝0.819 731 735，意味着虫口数以此八点周期变动。

当μ继续增大，在μ＝3.564 407 266处，系统分岔为16周期；在μ＝3.568 759 420处分岔为32周期；在μ＝3.569 691 610处分岔为64周期，等等。

可以严格证明，当μ≥μc＝3.569 945 972…时，系统的迭代结果是一系列的随机数。μ＞μc，便是系统的混沌区，在这个范围内系统的定态行为表现为随机运动（表2-2）（图2-5）。

图2-5　混沌：确定性非线性系统的内在随机

上述讨论表明，即使像虫口模型这样完全确定性的简单系统，没有外部随机作用，没有随机系数，初始条件也是确定的，系统自身竟然由于内在的非线性机制作用而自发地产生出随机性。它是确定性系统内固有的特征，因而被称为“内在随机性”（intrinsic stochasticity），也叫内秉随机性或自发随机性。

这就是1976年数学生态学家罗伯特·M·梅所发现的一种极为有趣的现象，严格的确定论的迭代，最终导致了非确定论的结果。这样便可以定义：混沌是一种确定性的随机性，即确定性系统内在产生随机性。

发现“确定性的随机性”非但具有重大的科学价值，而且具有重要的哲学意义。

4.决定论与概率论对立的终结

决定论自古以来有之。古希腊哲学家留基伯及其继承者德谟克利特是决定论的先驱，留基伯说：“没有一种事物的产生是无缘无故的，一切事物的产生都是有一定根据的，都是必然的。”18世纪法国唯物主义哲学家P·H·D·霍尔巴赫说，“我们所见的一切都是必然的”，“在这个自然之中，既没有偶然，也没有任何意外的事情”。决定论认为事物的运动变化有确定的因果联系之必然性、普遍性。

与决定论相反，非决定论是一种否认因果联系的必然性、客观性、普遍性的理论，认为事物发展变化完全是意志自由的。1970年，法国生物学家J·莫诺在发表的《偶然性与必然性——略论现代生物学的自然哲学》一书中认为：“只有偶然性才是生物界中每一次革新和所有创造的源泉。进化这一座宏伟大厦的根基是绝对自由的，但又是盲目的纯粹偶然性。”⁽⁷⁵⁾他说：“宇宙里可能出现的一切事件中间，任何一个可能出现的具体事件预先决定它出现的几率，总是接近于零的。”⁽⁷⁶⁾在这种意义上，他称自己的哲学是“一个无因果关系的宇宙哲学”。

300多年前，I·牛顿首次用微分方程等精确的数学工具来描述自然界的运动规律，将人们引导进了可预测性及有序的观念中。这种观念的不断发展，使人们产生了机械决定论的自然观。机械论解释的本质是把将来和过去看作是可以根据现在计算出来的，因而认为一切都是给定的。那些相信机械论的解释具有完美的客观性和普遍性的学者们，无论有意的还是无意的，都提出这种假设。19世纪初，P·S·拉普拉斯将这种决定论概括为：宇宙的现在状态是它们以前状态发展的必然结果，同时又是以后状态的形成原因。他在《概率论的解析理论》（1812年）一书中写道：“设想有这样一个‘智神’（intelligence），他不仅知道一定时刻支配宇宙运动的所有作用力和组成宇宙的一切实体的位置，而且还具有对这些资料能够进行分析的巨大能力，那么无论是最大的天体运动还是最小的原子运动都将包括在同一公式里。对于这样的‘智神’来说，没有任何不确定的事物，未来和过去都会展现在他眼前。”⁽⁷⁷⁾这就是著名的“拉普拉斯决定论”。

几乎与牛顿发展经典动力学决定论的同时，J·伯努利等人也建立起关于随机性的概率理论。于是概率论的自然观与决定论的自然观一直处于对立之中。尤其是20世纪量子力学的创立更加剧了这种对立，人们似乎必须对“上帝是否在掷骰子”作出判断。

1944年9月7日，A·爱因斯坦在给M·玻恩的信中表达了他与M·玻恩不同的观点：“你信仰掷骰子的上帝，我却信仰客观世界中的完备的定律和秩序”，他说：“甚至量子力理论开头所取得的伟大成就也不能使我相信那种基本的骰子游戏。”⁽⁷⁸⁾

由于确定论的思想自I·牛顿以来根深蒂固，以至对于物理学中统计描述的必要性，长期以来有两种对立的解释。

1989年1月3日，著名物理学家杨振宁在香港大学作“爱因斯坦和现代物理学”演讲时答问：

问：你认为我们是生活在一个概率性的宇宙中，还是在一个决定性的宇宙中？

答：哦，这是个非常重要的问题。我不知道怎样来直接回答你的问题，因为这涉及你怎样理解概率性和决定性的问题⁽⁷⁹⁾。

混沌理论的发展避免了人们的这种尴尬，因为它向世人展示了一个决定论系统在确定输入带有微小扰动的情况下产生了类似于随机的输出。在最初的惊讶过去以后，人们逐步接受了这样的观点：随机性存在于确定性之中，确定系统具有内在随机性（与经典理论不同的是，经典理论认为，系统的随机性来自系统外部）。这一发现似乎有利于概率论的自然观。“我们必须放弃现象——包括基本现象——是被严格决定的并可精确预言的那种传统观念，而代之以一种比较灵活的观念。这种比较灵活的观念就是承认在每一时刻在我们能够实现的基本现象的演化过程中存在着各种不可预测的事件，对于这些不可预测的事件，我们只能估计出它们出现的相对几率。”⁽⁸⁰⁾

然而，我们必须注意的是：混沌理论并没有简单地否定决定论，而是否定了机械决定论。当系统的输入可以无限精确地确定，则系统的输出（理论上）仍然是可预测的，只是这种预测不具有物理上的可实现性，我们对自然界的认识必须仍然建立在因果决定论的基础上。并且在实际中，对系统行为在有限时间范围内进行有限精度的预测仍然是可能的。因而，经典决定论与经典概率论的对立是基于无穷过程的，但人们实际的测量和计算只能达到有限步骤和精度，因而只要建立有限性原则（有限的测量精度、有限的观察时间等等），就可以消除两者的对立。

确定系统内禀随机性的发现，正在消除争论了300多年的决定论自然观与概率论自然观之间的鸿沟。现在知道，只要确定论的系统稍微复杂一些，它就表现出随机行为。牛顿力学具有内在的随机性。确定论和概率论描述之间，存在着由此及彼的桥梁。

5.自相似性：分形理论和菲根鲍姆常数

（1）具有自相似性的形态、结构、功能和信息：分形理论

分形理论（fractal theory）是关于分形性质及其应用的理论。由美籍法国数学家B·B·曼德勃罗于1977年出版的《分形、形态、机遇和维数》和1982年出版的《自然界的分形几何》中提出。最初，只限于研究形态或结构上存在自相似性的几何对象，故称为“分形几何学”（fractal geometry）。“fractal”一词源于拉丁文fractus，与英文fraction（碎片或分数）及fractured（断裂）具有相同的词根，其意义为“不规则的”或“支离破碎的”。国内学者曾将之译为“分数维”、“分维体”等，现在大多译为“分形”。B·B·曼德勃罗把“分形”定义为豪斯道夫-贝西科维奇维数严格大于拓扑维数的集合。

标志B·B·曼德勃罗思想转折的是一篇论文标题中所提出的一个问题：“英国的海岸线有多长？”为了研究曲曲折折的海岸线，英国科学家路易斯·里查逊曾经查阅了西班牙、葡萄牙、比利时、荷兰的百科全书，发现它们记载的边界线长度都有20%的误差。B·B·曼德勃罗论证的是：任何海岸线，从某种意义上说都是无限地长。答案取决于所用的尺度。用海里计算的长度，同真实的长度只是一种近似，其实还有许多细小的弯曲被忽略了。如果换成米来计算，或用厘米来量度，则必然得出更长的海岸线。这也就是说，随着标度的缩小，海岸线长度无限增大，小海湾内有更小的海湾，小半岛外有更小的半岛，直到分解为原子也许才会有终点。由此可见，海岸线也是无限复杂的现象。他把这种小标度上重现大标度的自相似现象，叫做分形。于是，他又给出了定义：其组成部分与整体以某种方式相似的“形”，叫做“分形”⁽⁸¹⁾。

分形是线性变换下的自相似性或非线性变换下的不变性。通常是指一类具有伸缩对称性而难以用传统几何学来描述其形态的对象。传统几何学描述的对象是由直线或曲线、平面或曲面、平直体或曲体构成的各种几何形状，称为整形。传统观点把自然界想象成各种规则形体的总和，但普遍存在的几何对象是分形，整形倒是一种例外。分形概念是对自然界普遍存在的复杂几何形体的科学概括。自然界中分形体无处不在，诸如变幻莫测的云彩、逶迤连绵的山脉、支流纵横的水系、蜿蜒曲折的海岸线，等等。自然界中这众多事物，具有自相似的层次结构，在理想的情况下，甚至是无穷多层次。适当地放大或缩小几何尺度，整个结构并不改变。分形几何学就是研究这些在形态或结构上存在自相似性（self‐similarity）的几何对象的。

自相似性，是分形最重要的特性。在分形几何学中，自相似性是指局部的形态与整体的形态相似，在一定的程度上，部分是整体的再现和缩影。

之后，随着研究的需要和来自系统论、控制论、信息论等方面的冲击，分形几何学也就被拓展、发展为“广义分形”。20世纪80年代末，一般把在形态、结构、功能、信息等方面具有自相似性的研究对象统称为“分形”。

按照分形理论，分形内部任何一个相对独立的部分，在一定程度上都应是整体的再现和缩影。人们把构成分形整体的相对独立部分称为“分形元”（fractal unit）或“生成元”（general）。分形理论阐述了“分形元”构成整体所遵循的原则与规律。

按目前研究水平，分形可分为自然分形、时间分形（亦称过程分形或重演分形）、社会分形和思维分形四大类。其中每一类还可进一步细分，如自然分形可分为几何分形、功能分形、信息分形和能量分形等。此外，还有递归分形（recurrent fractal）、自仿射分形（self‐affine fractal）、多重分形（multifractal）等，它们表征了自然界中一些不规则的非线性特征。几何分形又可进一步分为线状分形（如科赫曲线）、表面分形（如谢尔宾斯基地毯）、体积分形（如谢尔宾斯基海绵）。

现代动力学理论的研究发现，混沌动力学中的奇怪吸引子正是一种分形，它是隐藏在混沌现象背后的具有嵌套的自相似几何结构。分形理论所反映的分形形体具有同混沌完全相同的特性。

当我们观察映射和奇怪吸引子复杂图形时，便感到这些曾经是陌生的图形是不能用我们熟悉的欧几里得几何方法来描述的。在平直的欧氏空间中，点、线、面、体和由它们构成的规则的几何图形都有整数维和测量其大小或几何性质的特征尺度。测量的对象不同，采用的尺度单位也不同。既不便用尺来量万里长城，又不宜用寸来测大肠杆菌，前者失之太短，后者又嫌太长，所谓“夫尺有所短，寸有所长”（《楚辞·卜居》）就是这个意思。然而，具有无穷嵌套的自相似结构的映射图形和奇怪吸引子的复杂形态，无论怎样变换观测的尺度，局部仍然保持了整体的性质，特征尺度的作用失效了。

图2-6所示为一单位科赫（Koch）曲线。从这一曲线的画法可见，它就是以三角形作为自相似基本结构的分形。它的边界的总长度从3变成了3 × 4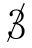，又变为3 × 4 × 4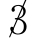，…，如此下去，最后以∞为极限。但是雪片的总面积始终保持在最初三角形的外接圆之内，因此这是一个无限长的边界线包围一个有限面积的数学例子。

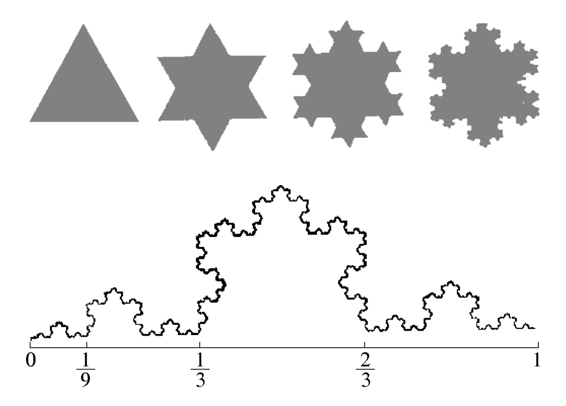
图2-6　科赫曲线

刻画整形的主要特征量如长度、面积、体积等，对于刻画分形是没有意义的。用不同的丈量单位测量同一海岸线，得到的结果显著不同。这是因为，若以千米为单位，则几十米以下的曲折将被忽略；若以米为单位，则厘米数量级以下的曲折将忽略。分形的主要几何特征是关于它的结构不规则性和复杂性，主要特征量应是关于这种不规则性和复杂性程度的度量。这就引出分数维数（简称分维）的概念。(www.xing528.com)

整形几何学研究的都是具有整数维的对象，点是零维的，线是一维的，面是二维的，体是三维的。抽象空间的几何对象也都是整数维的。即使将这样的几何对象连续地拉伸、压缩、扭曲、折叠，维数也不会改变。这就是所谓拓扑维，用字母d表示。

分维则是扩展了维数的概念，用字母D记之，它可以是整数，也可以是非整数，一般情况下是一个分数。

从维数这一性质看，分形的基本特征是它的分数维不小于它的拓扑维，即D≥d。

分维是分形几何对象不规则或复杂性程度的量度。由于复杂性的类型很多，需用不同定义的分维概念来表示，从不同的角度刻画它的不规则性。目前，人们已经提出多种分维定义，如容量维、信息维、关联维等。

这里介绍由F·豪斯道夫引入的维数定义。

把一个D维几何图形的每一个独立方向放大λ倍，可得到N个原来未放大的图形（ N＝λ^D），则有

我们用它计算科赫雪花曲线的分维。根据豪斯道夫维数定义，若将［0，1］区间的科赫曲线放大9倍，可得原大小的科赫曲线，或者说原科赫曲线包含了16个［0，1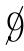］区间的科赫曲线。由此求得科赫曲线的维数

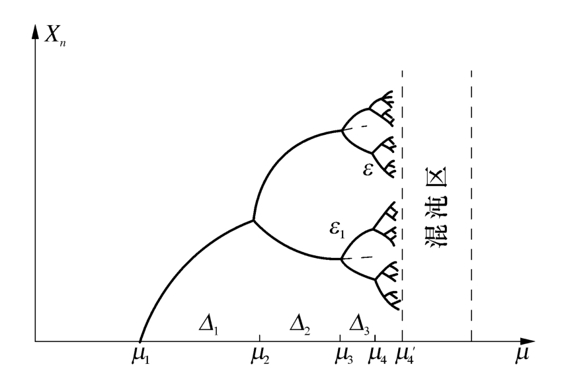
图2-7　倍周期分岔的自相似性

（2）分岔的自相似性：菲根鲍姆常数

美国物理学家M·菲根鲍姆进一步研究了倍周期分岔现象，于1976年发现了隐藏于其中的一种规则性，即分岔中存在的两个普适常数δ、α。其研究结果发表于美国《统计物理学杂志》1978年第19卷上。

如图2-7所示，随着控制参量μ的增加，横轴方向的倍周期分岔间距Δ₁，Δ₂，…渐进地按因子δ衰减：

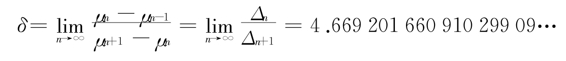
也就是说，前一个分岔间距是后一个分岔间距的4.669 201 660 910 299 09…倍。这个无理数称为菲根鲍姆δ常数。

再一个发现是刻画标度律的普适常数。即随着控制参量μ的增加，纵轴方向的分岔宽度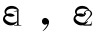，…渐进地按因子α衰减：

也就是说，前一个分岔宽度为后一个分岔宽度的2.502 907 875 095 892…倍，这个无理数称为菲根鲍姆常数α。

M·菲根鲍姆对其他一些单值映射也做了计算，如

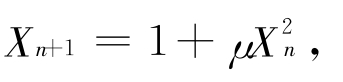
X_n＋1＝μsin（πX_n），　　　

X_n＝1＝X_nexp［μ（1－X_n）］。

M·菲根鲍姆通过计算证明，虽然这些映射迭代关系不同，但所得的参数关系极限值都是一样的。这说明菲根鲍姆常数不是个别特殊的现象，而是一类分叉现象中的普遍数量特征。它们和常数π与e一样，是反映自然本质的两个新的普适常数。据此，系统的分岔行为不仅可以定性地证明，而且可以定量地计算，不仅表现在方式上，而且表现为精确的数字和规律性。它表明在自然系统的演化过程中，其几何图像与分岔图均具有无穷嵌套的自相似几何结构，即自然事物整体具有其部分相类似的结构，或同一种行为在愈来愈小的尺度上重复出现。这种自相似性不是两个无关事物之间的偶然相似，而是在系统演化中必然出现并始终保持的。

现代动力学理论的研究发现，混沌动力学中的奇怪吸引子正是一种分形，它是隐藏在混沌现象背后的具有嵌套的自相似几何结构。分形理论所反映的分形形体具有同混沌完全相同的特性。混沌区也具有错综复杂的结构，比人们所想象的远为有序。仔细分析，在混沌区内互相嵌套的大大小小的层次类似洋葱头或套箱，具有彼此相似的结构，称为“自相似结构”。这些“自相似结构”无穷无尽地互相套叠，从而形成了“无穷嵌套自相似结构”。对于混沌区的这种“无穷嵌套自相似结构”，可以用电子计算机描述出来，它的花样层层套叠，异常奇妙，可称为“混沌美”。任何部分被放大以后，看起来都与整体相似。

分形理论与菲根鲍姆常数揭示了分形元构成整体所遵循的原则和规律，发现了从部分过渡到整体的媒介与桥梁，提出了作为整体的系统“分”为部分和从部分出发认识整体的原则与方法，揭示了复杂性背后隐含的统一性，为在复杂系统中发现规律性，探索自然界系统的形成和演化发展，研究混沌中的有序开辟了道路。它从一个特定的层面直接揭示了宇宙的统一图景，指出每一个元素都反映和含有整个系统的性质和信息，即元素映现整体以及部分与整体之间的多层面、多视角、多维度的关联方式，为人们认识世界提供了崭新的方法论。

【注释】

(1)罗素：《人类知识》，商务印书馆1983年版，第42页。

(2)埃里克·詹奇：《自组织的宇宙观》，中国社会科学出版社1992年版，第87页。

(3)《马克思恩格斯选集》第4卷，人民出版社1995年版，第244页。

(4)E.Mayr.Toward a New Philosophy of Biology.Harvard University.Press，1988，p.162.

(5)E·拉兹洛：《进化——广义综合理论》，社会科学文献出版社1988年版，第1页。

(6)参见本章第三节。

(7)罗素：《西方哲学史》上卷，商务印书馆1963年版，第191页。

(8)亚里士多德：《物理学》，商务印书馆1982年版，第136页。

(9)同上书，第132页。

(10)亚里士多德：《物理学》，商务印书馆1982年版，第220页。

(11)同上书，第127页。

(12)同上书，第123页。

(13)同上书，第125页。

(14)康德：《纯粹理性批判》，商务印书馆1960年版，第55页。

(15)同上书，第56页。

(16)亨利·柏格森：《创造进化论》，商务印书馆2004年版，第216页。

(17)同上书，第285页。

(18)伊·普里戈金：《从存在到演化——自然科学中的时间及复杂性》，上海科学技术出版社1986年版，第186页。

(19)同上书，第197页。

(20)伊·普里戈金：《确定性的终结——时间、混沌与新自然法则》，上海科技教育出版社1998年版，第20页。

(21)同上书，第43页。

(22)同上书，第130页。

(23)同上书，第133页。

(24)亚里士多德：《形而上学》，商务印书馆1959年版，第68页。

(25)北京大学哲学系外国哲学史教研室译：《西方哲学原著选读》上卷，商务印书馆1982年版，第139页。

(26)亚里士多德：《形而上学》，商务印书馆1959年版，第55页。

(27)列宁：《哲学笔记》，人民出版社1993年版，第195页。

(28)北京大学哲学系外国哲学史教研室编译：《西方哲学原著选读》上卷，商务印书馆1982年版，第141页。

(29)W·海森堡：《物理学和哲学》，商务印书馆1981年版，第11页。

(30)W·海森堡：《严密自然科学基础近年来的变化》，上海译文出版社1978年版，第177页。

(31)洪定国：《戴维·玻姆的科学思想与方法》，光明日报出版社1990年版，第193页。

(32)保罗·戴维斯：《上帝与新物理学》，湖南科学技术出版社1992年版，第28页。

(33)惠勒：《物理学与质朴性》，安徽科学技术出版社1982年版。

(34)W·I·B·贝弗里奇：《发现的种子》，科学出版社1987年版，第95页。

(35)R·G·柯林武德：《自然的观念》，北京大学出版社2006年版，第99～100页。

(36)埃里克·詹奇：《自组织的宇宙观》，中国社会科学出版社1992年版，第269页。

(37)“盖娅”（Gaia），原是指古希腊神话中的大地女神，古希腊人用这一词来指称生养万物的大地。1979年，英国化学家拉夫洛克在其著述的《盖娅：关于地球生命的新视角》一书中，运用生物化学的理论，提出著名的“盖娅假说”。在这个假说中，“盖娅”被定义为“能够自我维持、自我塑造的系统”。

(38)埃里克·詹奇：《自组织的宇宙观》，中国社会科学出版社1992年版，第270页。

(39)埃里克·詹奇：《自组织的宇宙观》，中国社会科学出版社1992年版，第87页。

(40)康德：《实践理性批判》，商务印书馆1960年版，第166页。

(41)《马克思恩格斯选集》第2卷，人民出版社1995年版，第29页。

(42)W.K.C.A Guthrie.History of Greek Philosphy.Cambridge.Volume1-The Earliev Presocratics and the Pythagoreans，Reprinted 1971.p.90～91.

(43)G.Gamow.Physical Review，1948，74，p.505；R.A.Alpher，R.C.Herman，and G.Gamow，Physical Review，1948，74，p.1198.

(44)Alan H.Guth and Paul J.Steinhardt.The Inf lationary Universe，Scientific American.May 1984.

(45)根据E·特赖恩“免费午餐”的思想，“我们的宇宙”具有两种能量形式，一种与引力有关，是负能量；一种与质量有关，是正能量。宇宙的总能量可能是零，对应于宇宙空无一物时的状态，即正负能量相等。由于不稳定性的存在，便有可能引力是与时空曲率相联系的，因此时空可以产生物质。

(46)陈其荣：《自然哲学》，复旦大学出版2004年版，第90～91页。

(47)《马克思恩格斯选集》第3卷，人民出版社1995年版，第422页。

(48)同上书，第413页。

(49)M·艾根、P·舒斯特尔：《超循环论》，上海译文出版社1990年版，第222页。

(50)《马克思恩格斯选集》第1卷，人民出版社1995年版，第67页。

(51)《马克思恩格斯全集》第20卷，人民出版社1971年版，第509页。

(52)同上书，第515页。

(53)同上书，第509页。

(54)《马克思恩格斯全集》第20卷，人民出版社1971年版，第511～512页。

(55)陈其荣：《自然哲学》，复旦大学出版社2004年版，第101页。

(56)I·普里戈金：《确定性的终结》，上海科技教育出版社1998年版，第54～55页。

(57)同上书，第57页。

(58)E·拉兹洛：《进化——广义综合理论》，社会科学文献出版社1989年版，第43页。

(59)金吾伦：《生成哲学》，河北大学出版社2000年版，第168页。

(60)R.W.Sperry.Neurology and the Mind‐Brain Problem.A merican Science，Vol.40，1952，295.

(61)马里奥·邦格：《科学的唯物主义》，上海译文出版社1989年版，第27页。

(62)J·L·卡斯蒂：《虚实世界》，上海科技教育出版社1998年版，第90页。

(63)Jeffrey Goldstein.Emergence as a Construct ：History and Issues.Emergence ：The Journal of Complexity in Management and Organization.1999，Vol.1，52.

(64)L·贝塔朗菲：《一般系统论》，社会科学文献出版社1987年版，第46页。

(65)达尔文：《物种起源》，商务印书馆1995年版，第538页。

(66)E·拉兹洛：《进化——广义综合理论》，社会科学文献出版社1988年版，第79～81页。

(67)D.T.Campbell，Downward Causation.Hierarchically Organized Biological Systemes.In Studies in the Philosophy of Biology，F.J.Ayala & T.Dobzhansky （ed.）Macillan Press.1974.176.

(68)H·庞加莱：《科学与方法》，辽宁教育出版社2001年版，第39～40页。

(69)《马克思恩格斯选集》第4卷，人民出版社1995年版，第244页。

(70)这一非线性模型是20世纪50年代澳大利亚生态学家W·E·里克首先在饲养鱼类的研究中提出来的。

(71)亨利·柏格森：《创造进化论》，商务印书馆2004年版，第38页。

(72)同上书，第39页。

(73)同上书，第45页。

(74)“3”是系统演化发生的第一个分支点，因而“3”即意味着演化，意味着复杂性，意味着万物创生。

(75)J·莫诺：《偶然性与必然性——略论现代生物学的自然哲学》，上海人民出版社1977年版，第84页。

(76)同上书，第107页。

(77)Philipp Frank.Philosophy of Science : The Link Between Science and Philosohy.Englewood Cliffs，N.J.：Prentice‐Hall，1957.p.263.

(78)许良英、范岱年编译：《爱因斯坦文集》第1卷，商务印书馆1976年版，第415页。

(79)宁本治等主编：《杨振宁演讲集》，南开大学出版社1989年版，第398～399页。

(80)P·德布罗意：《宏观物理学与微观物理学》，商务印书馆1992年版，第179页。

(81)B.B.Mandelbrot.The Fractal Geometry of Nature.Freeman，New York，1997.