【摘要】:图2—2香农—韦弗数学模式在这个模式中,信源从一组可能传播的消息中产生出实际传播的一条消息,这个消息可能由口头语或文字、音乐、图像等组成。
二、香农与韦弗模式的技术观
克劳德·香农与韦弗(Clavde Shannon&Weaver)的《传播学的数学理论》(Mathematical Theory of Communication,1949)已成为其他传播模式和理论发展的最重要及最有影响的促进因素,香农与韦弗模式的最大特点是从技术的角度出发,根据是信号传输的统计学概念(这种概念最先是由维纳强调的),提出了“噪音源”的概念,形成了“香农—韦弗数学模式”(见图2—2)。在《传播学的数学理论》的第二部分,韦弗提出了传播的简图,由此产生了其他许多传播过程模式。
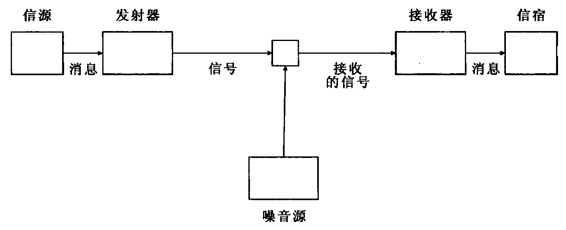
图2—2 香农—韦弗数学模式(https://www.xing528.com)
在这个模式中,信源从一组可能传播的消息中产生出实际传播的一条消息(message),这个消息可能由口头语或文字、音乐、图像等组成。发射器(transmitter)将消息转变为信号以适合传播渠道使用。渠道(channel)是将信号(signal)从发射器传送到接收器的传送中介。在人际传播中,信源是大脑,发射器是制造信号(口语)的发音器官,通过空气渠道送传。
香农和韦弗的另外一个主要贡献就是在消息中包括了熵(entropy)和冗余(redundancy)的概念。为达到有效的传播,两者之间就应保持平衡,以抵消传播渠道中的杂音。简单说来,传播渠道中的噪音越多,就越需要冗余,这样就降低了消息中相对的“熵”值,例如,在嘈杂的渠道传送无线电信息时,需要重复关键的部分,以确保信息的接收,如“星期二将抵达,重复星期二”。通过冗余来克服传播渠道中的噪音,在特定时间内可传送的信息量就会减少。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




