玉米秸秆微晶纤维素制备工艺

2.2.2　玉米秸秆微晶纤维素制备工艺的响应面优化

2.2.2.1　微晶纤维素制备工艺试验设计与结果

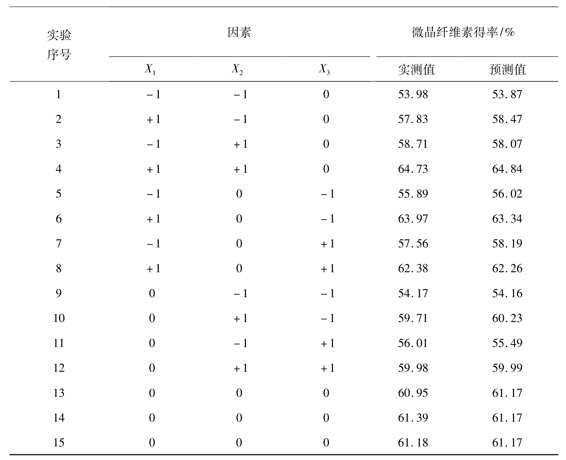
根据Box－Behnken试验设计原理，用硫酸浓度X₁、水解温度X₂、水解时间X₃3个因素水平，设计了15个试验点的响应面分析试验。试验方案和结果见表2.4。

表2.4　试验设计及其结果

2.2.2.2　微晶制备过程模型建立与显著性检验

利用SAS统计分析中的RSREG(response surface regression)程序对15个试验点数据进行回归计算，建立二次多项式回归模型，如下面方程所示，并对回归方程进行方差分析和方程系数显著性检验，结果见表2.5。

Y=61.173+2.85A+2.64B+0.27C+0.54AB－0.82AC－

0.40BC+0.06A²－2.42B²－1.28C²

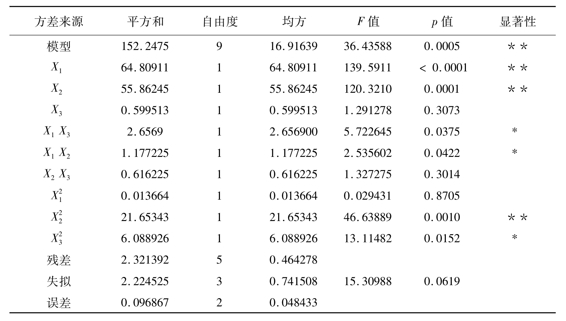
该方程的回归系数R²=0.9849，说明所建立的模型能很好反映试验数据，回归方程的拟合度较好，试验误差小。在显著水平(p＜0.05)条件下，基于回归方程的因素显著性分析，模型中一次项硫酸浓度X₁(p＜0.0001)、水解温度X₂(p=0.0001)、二次项X₁X₃(p=0.0375)、X₁X₂(p=0.0422)、X₂X₂(p=0.0010)、X₃X₃(p=0.0152)和X₂X₃(p=0.3014)均表现显著，一次项水解时间X₃(p=0.3079)、二次项X₂X₃、X₁X₁表现不显著。模型的失拟项p=0.0619＞0.05，表明失拟不显著，即该模型是稳定的，能较好地预测实际玉米秸秆微晶纤维素得率的变化情况。因此，可以采用此模型对微晶纤维素得率进行分析和预测。

表2.5　响应面回归方程方差分析

2.2.2.3　微晶制备过程响应面分析与优化(www.xing528.com)

用Design－Expert软件，根据回归方程分析作响应面图2.6～图2.8，分析硫酸浓度、水解温度、水解时间对微晶纤维素得率的影响。

从图2.6可以看出，硫酸浓度与温度的交互作用较显著。随着硫酸浓度的增大，微晶纤维素的得率也随之上升。当硫酸浓度达到60%时，微晶纤维素的得率达到最大。对于水解温度而言，随着水解温度的增加，微晶纤维素的得率呈先增加后下降趋势。

从图2.7可以看出，硫酸浓度与水解时间的交互作用显著。当水解温度不变时，随着硫酸浓度增加和水解时间的延长，微晶纤维素得率呈递增趋势。在硫酸浓度为60%，水解时间约80.56 min时达到最大，随后下降。这可能是由于在高浓度硫酸存在时，随着水解时间的延长，部分微晶纤维素会被进一步水解。

从图2.8可以看出，温度与时间的交互作用不显著。当硫酸浓度不变，随着水解温度的增加和水解时间的延长，微晶纤维素得率呈现增加的趋势。当水解温度为56.84℃和水解时间为80.56 min时，微晶纤维素得率最大。这可能是由于在高浓度硫酸存在时，随着水解温度升高和水解时间的延长，部分微晶纤维素会被进一步水解。

图2.6　硫酸浓度与水解温度对晶体得率的影响

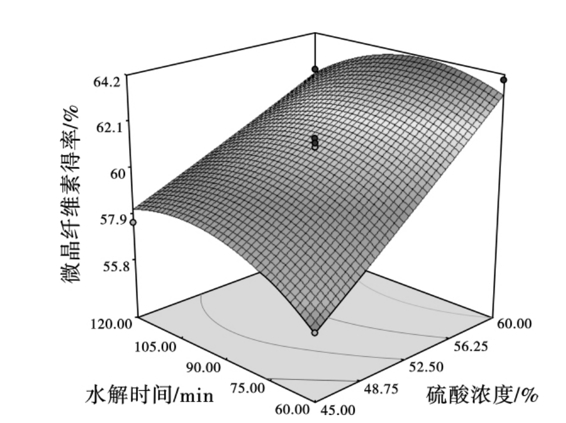
图2.7　硫酸浓度与水解时间对晶体得率的影响

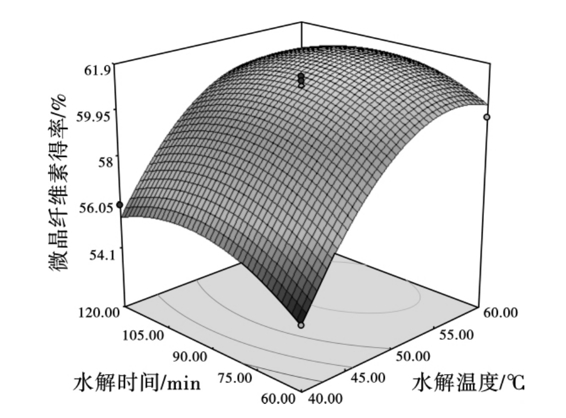
图2.8　水解时间与温度对晶体得率的影响

2.2.2.4　微晶制备过程最佳工艺条件确定及验证试验

基于以上响应面分析，通过软件模拟寻优，当硫酸浓度60%、水解温度56.84℃和水解时间80.56 min时，微晶纤维素得率达到最大值65.25%。考虑到实际操作性，将玉米秸秆微晶纤维素酸法制备工艺修正为:硫酸浓度60%、水解温度57℃和水解时间80 min。为了检验模型预测的准确性，依据修正的最佳工艺条件进行玉米秸秆纤维素硫酸水解试验，3次重复，微晶纤维素的得率平均值为66.85%。试验值与模型优化模拟值基本一致，并获得较高的微晶纤维素得率，表明优化模型有较好可靠性。