高科技企业创业管理提要

第七章　高科技企业创业融资

一、高科技创业企业的融资行为

高科技创业企业的融资行为，是在其整体发展策略中，对外寻求合作资源的过程。例如我国著名的高科技创业企业盛大网络，前后两次融资的选择对象，分别是中华网（300万美元，2000年）和软银亚洲（4000万美元，2003年）的风险资金，特别是其2003年选择“软银亚洲”是在年营业额达到6．8亿元，纯利1亿元的基础上做出的决策，与其说主要考虑的是资金支持，还不如说对其成功上市并获得公开发行的追捧效应的帮助作用是最重要的考虑因素。

形成高科技创业企业股权关系行为的来源主要有两个。一是股权增资行为，通常发生在高科技创业企业的需求主要为财务资源并采取股权取得方式时。二是当其需求属于综合资源需求时，高科技创业企业在考虑诸多潜在对象之间资源特征后，也会采用股权方式合作。因此，在分析高科技创业企业的融资行为时，可以从资源需求的类型着手。

对高科技创业企业而言，无论是为了取得哪种资源而进入股权合作关系架构，都会被自身的资源特性以及希望合作对象的资源特性所影响。在股权关系中，无论各方股权比重如何，彼此都会进行较为频繁的接触与紧密关系，随着彼此的了解与配合默契的增加，资源利用的效率也会提高。特别对于拥有知识型资源的企业而言，在这样的合作架构中知识资源的流动与学习效果会比较明显。因此，对于核心资源为知识型资源的高科技创业企业，无论用哪种资源与外部进行交换，企业自身都会考虑如何保护其知识型核心资源，这样就可能会采取以下两种方式：

（1）避免进入股权合作关系，或等到高科技创业企业知识型资源的外溢或被模仿的障碍较高后才选择股权合作关系。

（2）降低股权关系对企业自身的影响，这样毫无疑问会影响股权合作对象的决策，同时也可能会倾向于选择进入比较容易的少数股权合作者。

对于核心资源为知识型资源的高科技创业企业而言，进入股权合作关系的目的不在于取得或应用其他高科技创业企业的核心资源，而是为取得未来发展所需的财务资源。因此与一般风险投资公司合作，对于知识型高科技创业企业而言，便是最佳的选择之一。

至于核心资源为财务资源型的高科技创业企业，由于股权关系的建立会加速其吸收和学习知识资源，同时又不用担心自身的财务资源会被合作方“模仿”或“学习”，因此，这样的高科技创业企业将会选择尽早进入股权合作关系，而且允许外部股东所占的权重也会比知识型企业为高，因为这样会使交易双方更快速地投入更多的资源，以提升合作绩效。可以说，初始核心资源类型会影响到创业期间整体的融资行为。

高科技创业企业的初始核心资源特性，对创业期间整体融资行为有着不可忽略的影响。对于知识型高科技创业企业，其整体融资策略，主要在于确保核心资源不被合作对象所模仿或应用资源的方式（能力）受到干扰。在创业时期，企业的股权合作对象会较为单纯；同时，会较晚地应用外部的股权关系。而对于财务资源型高科技创业企业，其整体融资策略，主要在于应用此关系而快速取得成长所需资源。因此，在创业时期，高科技创业企业的股权合作对象会较为多元，同时会较早使用外部的股权关系。

在有关股权关系形成原因方面，当高科技创业企业主要的需求资源为财务资源时，高科技创业企业由于无法通过接触公开要素市场取得所需资金，因此会倾向于采用战略联盟方式替代之。也就是说，战略联盟会成为取得财务资源的手段之一。以战略联盟方式取得财务资源，已成为新创事业或是科技密集产业的特性之一，并已经成为新创高科技企业早期种子资金的来源。这里的战略联盟可以定义为，某一成熟的企业与一处于早期发展阶段的科技企业的合作关系，后者加入联盟的目的在于追求种子资金以促进企业成长，而前者则是希望通过彼此的合作，使组织运作更具弹性，或是增加创新能力，或是达到资源互补目的。而当前的现实状况也证明，以战略联盟方式取得资金，会是创业者的首选，同时也可给创业者提供最大的协助。战略联盟虽然可以归为筹资策略的手段之一，但同时，这样的战略联盟并不只是设计用来取得风险资金的渠道，也追求互补的有形与无形资产，如具体的技术、专利、经营能力及销售渠道的网络关系等。因此，高科技创业企业在选择合作对象时，还是会选择策略发展伙伴的概念来进行，即公司的核心资源在此将具有重要的影响。

当高科技创业企业以资源需求为综合型资源时，企业取得外部资源的流程就与发展新产品流程雷同，而此时股权关系的形成原因，主要受到两个要素影响：一是企业本身的主要交换资源类型，二是对方主要交换的资源类型。但前提都是高科技创业企业必须掌握决定关系的权力。

当高科技创业企业的主要交换资源为知识型资源时，其会倾向于与主要交换资源为财务资源型的企业建立少数的股权关系。因对高科技创业企业而言，合作对方股权的投入降低其的投机程度，防止其在学习知识型资源后便迅速结束合约关系；而与具有知识型资源的企业建立合约基础关系，这样才可确保企业本身也能在学习之后，快速退出，而合作对象也选择同样的最优方式。而相对的，当高科技创业企业主要交换资源为财务资源型时，会选择建立股权比重较高的联盟关系，即希望对方投入较多的股权资金，因为这样才会使知识型资源充分地移动，且对方不必担心丧失资源的问题，因其拥有极高比重的企业股权。如企业因取得并应用其知识型资源而获得利益，则会充分反映在企业的价值，即股权价值方面。该类型的高科技创业企业则会与主要交换资源为财务资源型的企业建立薄弱的单向合约关系，以避免投入过多成本。当高科技创业企业资源需求为综合型时（即以非财务资源为主），个别股权关系的构建会受到主要交换资源类型的影响，即合作一方为知识基础型资源，另一方为财产权基础型资源时，则股权关系将随之产生。

二、高科技创业企业股权融资的实物期权评价

使用多期实物期权来衡量高科技创业企业股权融资的价值，能够反映传统会计方法所无法反映的“多期”与“高风险”特性。

（一）实物期权的内涵

Trigeorgis（1996）指出传统企业评估理论已经与现实出现了差异，公司决策阶层通常会自动增加传统投资评价模式所估出的价值，将营运弹性与策略考虑视为现金纳入其中。以折现净现金流量法为基础的评估方法，如净现值法，已受到诸多学者的质疑：如Pindyck（1991）认为，现金流量折现方法没有考虑到融资方案所具有的不可逆性与投资决策的可迟延性；Trigeorgis （1996）也认为，现金流量折现方法忽略了各投资期间序列交互相关的特性，无法适当地捕捉管理者对未预料到的变化做出反应的决策弹性。

在实物期权理论的分析架构下，可将传统评估理论所忽略的管理弹性及策略弹性纳入考虑（Trigeorgis，1996），同时兼顾到融资方案的不可逆性与投资决策的可迟延性（Pindyck，1991）。净现值法仅仅只是当净现值大于零时则实行否则就放弃的单向思考，实物期权方法则是同时兼顾考虑标的物的净现值及不确定性所蕴藏机会的系统性考量（Luhrmann，1998）。

关于实物期权理论的内涵，Luhrmann（1998）利用净现值比与累积变量构成期权空间，并将投资机会置于此空间中思考。他为了说明方便，定义了两种净现值：

（1）修正后的净现值：NPV＝S－PV（X）。

（2）净现值比：NPVq＝S／PV（X），其中PV（X）＝X／（1＋r）为利用无风险利率r折现的执行价净现值；当净现值比NPVq＞1，代表修正后净现值大于零，例如：S＝10，PV（X）＝8时，修正后NPV＝2，NPVq＝1．25＞1；反之，NPVq＜1，修正后净现值小于零。而累积变异数σ2 T为融资方案价值的变异数乘上时间T。随着时间增加，累积变异数上升，等待的价值提高，融资方案价值增加。在Luhrmann期权空间中，净现值比NPVq越高，累积变量越大（即原点往右下方射线的方向），融资方案的价值会越高，并以横轴NPVq＝1为中点，将期权空间划分为六个区块，如图7．1所示，代表不同“程度”的投资机会，它们分别是：立即投资、有可能会立即投资、有可能以后会投资、有可能过一段就放弃投资、很有放弃的机会、不可能会投资。

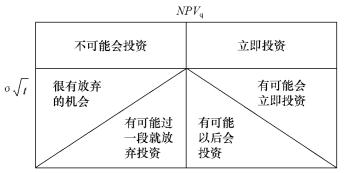
图7.1　Luhrmann期权空间

Luhrmann对期权空间的分类使得投资决策的可迟延性得到了完美体现：若NPVq＞1，且累积变异小，未来不太有其他变化，则这个融资方案可立即执行，就如同果园中那些已成熟的番茄，可立即采收；相对的，那些NPVq＜1，且累积变异小的融资方案，是不可能去执行的，就好像不会采收烂掉的番茄一般；而那些累积变异大，不确定性相对高的融资方案，可以等待新信息流入后再做决定，但NPVq＞1的方案更有机会得到执行，就像未成熟的番茄，现在不会立即采收，可以等待未来情况明确再做出决定。

传统的融资方案评估准则，如净现值法，净现值大于零则实行，否则放弃的决策思维在Luhrmann期权空间中只占有NPVq轴，是“一维”的考虑模式，但实物期权却是同时考虑到净现值与融资方案标的不确定性所蕴涵等待价值的“二维考虑模式”。

（二）实物期权的评价机制

传统期权评价机制的想法是通过有交易的标的证券（traded underlying securities）与由标的物衍生出来的衍生性商品（derivatives）形成一个无风险的投资组合，这个投资组合恰可复制期权的现金流量。Hull（1997）将交易证券（traded security）定义为由为数众多的投资人单为投资目的所持有的交易资产，如股票、证券、石油等皆为交易证券。在投资组合为无风险的状况下，其报酬恰为无风险利率（risk free rate），并且由于评价公式中的参数都与投资人的风险态度无关，因此风险中立的评价机制即可运用于此。

实物期权套用于金融期权的评价机制的最大问题在于，通常实物期权所评价的对象为非交易证券（nontraded security），Hull（1997）指出，一般而言当标的物为交易证券，风险中立的评价方法显示投资人的风险态度会与衍生性商品的价格与标的物的价格无关，然而若标的物为非交易证券，则投资人的风险态度则变得更为重要，因此传统金融期权评价机制是否整体都能够适用于实物期权，是应用实物期权理论做投资计划评估前所要仔细考虑的地方。

为了说明实物期权与金融期权在标的物有无交易方面对于评价机制所造成的差异，先来分析有衍生性商品的评价公式。

1．一般化的定价公式

Hull（1997）对连续时间下的衍生性商品定价模式有相当完整的描述，其中强调无论标的物有无交易，都可以适用于这个一般化的衍生性商品定价公式。这个定价公式的描述如下：给定一衍生性商品（F），其价值衍生自n个标的资产θi与时间变量t，假设标的资产θi的价值演化过程遵循几何布朗运动：

其中i＝1，2，…，n，αi，σi分别为标的物Vi的预期增长率与波动性，dzi为维纳过程的增量（increment of Wiener process），现在假设，在完美市场下，至少存在n＋1种交易证券，其价值为Fj（θ1，θ2，…，θn，t），为n个标的物与时间的函数，则dFj可表示为伊藤引理（Ito’s Lemma），其公式为：

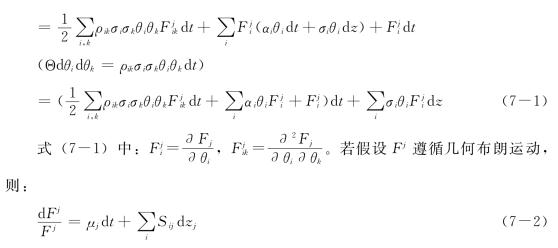
其中μj为衍生性商品Fj的预期增长率，Sij是由衍生性商品Fj中第i项标的物带来的瞬间波动函数。

将式（7－2）代入模型，可得：

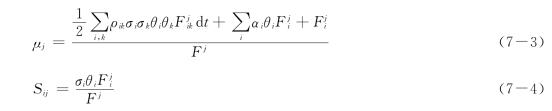
利用此n个标的物与n＋1种衍生性证券形成投资组合∏，令每一种证券j的投资权重为Wj，这样：

为了将式（7－5）中的不确定项消除，以建构一个无风险的投资组合，则必须等于0，而在无风险的假设下，投资组合的报酬率为无风险利率，因此在无套利的情况下也必须等于0。因此就有式（7－6）成立：

式（7－6）为多变量资产定价模型，其中参数λi＝（μi－r）／Si，（μi为总报酬，包括任何可能的股利率Di）是标的物资产的风险市价（market price of risk），可视为θi的风险估价（price ofθrisk），而可视为θi风险定量（quantity ofθrisk），而则表示无风险利率之外的风险贴水（risk premium），代表着投资人对资产i所需求的风险报酬。若资产i可以支付股利率Di，则预期的增长率μi＝αi＋Di，这样就可以得到风险贴水RPi：

RPi＝αi＋Di－r＝λiSij

同时，将式（7－3）的结果带入式（7－6）中，可得：

2．风险与报酬

在风险的调整方面，式（7－7）为基于无套利机制（arbitrage free argument）所得的衍生性商品基本定价偏微分方程，无论标的物交易与否都适用；Hull（1997）指出当θ不为交易证券时，若再使用风险中立的评估方法并无任何意义，而若能将标的物的预期增长率由α调整至α－λσ，这样一来即如同是在风险中立的环境下进行定价分析。Constantinides（1978），Cox，Ingersoll，and Ross（1985）讨论衍生性商品定价文献及McDonald and Siegel（1985），Trigeorgis（1993b）讨论实物期权的文献中都提出了相类似的观点。

Constantinides（1978）将存有市场风险的标的物转换到风险市价为零的环境中进行定价分析，其所使用的方法称之为固定对等法（certainty－equivalence approach），这一方法分为两个步骤：首先将模型中的参数调整到有效值（effective value），即扣除风险贴水，其次是将预期的现金流量以无风险利率折现，就如同是在风险市价等于零的状况。Constantinides（1978）以单一期间的范例做说明，假设x为期末将实现的现金流量，则使用Sharpe－Lintner资本资产定价模型而得的风险调整净现值RANPV（～x）将会是：

式（7－8）所描述的即为将预期的现金流量x调整到固定对等现金流量，再使用无风险利率Rf折现的过程。Cox，Ingersoll，and Ross（1985）对于不确定风险的调整也是使用固定对等法而不是风险调整过后的折现率，他们将实际的预期增长率修正为固定对等的增长率，修正的方法为用实际的预期增长率减除风险贴水。Constantinides （1978）引用Merton（1973）的文献指出，均衡的证券报酬必须满足资本资产定价模型的基本关系式：αi－r＝λmσim／σm＝λmρimσi，其中m指的是市场投资组合，而λm＝（αm－r）／σm。

基本上，Constantinides（1978）的推衍是在均衡模型下得到的，而式（7－7）却是基于无套利假设而得的，虽然推导的模型不一样，但并无矛盾之处，并且相辅相成，结论一致。如果资本资产定价模型的基本关系式成立的话，则λmρimσi便是资产i的风险贴水，而式（7－7）中αi－λiσi也表示资产i的风险贴水，因此λmρim＝λi，便成了资产i的风险市价。

同样的，Trigeorgis（1993）对于实物期权领域中标的物为非交易证券的衍生性商品的定价也有类似于固定对等方法风险调整的解释，他认为，对于资产的或有请求权（contingent－claim）定价，无论标的物是否可交易，都可通过由固定对等率（certain－equivalent rate）αCE替代真实增长率α的处理，在一个存在系统风险（systemetric risk）的环境下进行定价分析。这里的固定对等率也就是从原标的物的增长率扣除风险贴水（RP＝λσ），这样一来即如同是在风险中立的环境下进行定价分析。直观上，在风险中立的环境下所有资产的预期报酬为无风险利率（即不存在风险贴水），然而在投资者的风险态度为风险规避的环境下，均衡的预期增长率则会较原先的增长率来得低，即αCE＝α－RP。以上的调整方法就如同使用无风险利率来对现金流量折现，而不是使用风险调整后的利率对预期的现金流量做调整，换句话说，衍生性商品的现值F，可通过无风险利率来对风险中立的未来报酬FT加以折现，即为风险中立下的期望运算符，其中固定对等率αCE替代原先标的物的真实增长率α。

而在报酬的短差方面，对于非交易证券的定价机制，McDonald and Siegel （1984，1985）提出另一个有别于固定对等法的观点，但其实质并没有太大的区别。McDonald and Siegel（1984）指出正确的期权定价公式应符合两个条件：一是在到期日时间T上，公式的解应符合Max［0，FT－X］所得出的值；二是公式的解的期权价值应能表示期权所得的报酬并与资本市场均衡一致。然而实际上Black－Scholes公式解的值却与资本市场均衡的考虑相互独立，并无关联。因此，McDonald and Siegel（1984）主张正确的公式解中会存在一项与均衡报酬间的短差项（rate ofreturn shortfall）δ，也就是说当标的物资产本身不支付任何股息并且其预期报酬刚好等于市场要求的均衡报酬时，才会满足Black－Scholes偏微分方程。δ可由资本资产定价模型求得，形式为λmρimσi，其结论与Constantinides（1978）相似，也可以代入式（7－7）中。

因此McDonald and Siegel（1985）认为如果融资标的物在市场中并无交易，则其增长率α会低于由具有对等风险的交易证券（equivalent－risk traded security）市场要求的预期均衡报酬αs；而对等风险证券的期望报酬αs与标的物实际增长率间的差额δ（δ＝αs－α）类似于固定的股利率。由于非交易证券项中出现δ项，使得它与有交易的资产定价有所区别，因此，必须对δ项进行讨论，McDonald and Siegel（1985）对此有较为翔实的解释，他们首先举了非投资性资产——铅笔制造为例：假设铅笔的价格长期固定，而非随机性波动，并且制造铅笔的边际成本也是固定的，则铅笔的预期增长率α＝0；并且由于铅笔价格与生产的边际成本项目长期固定，因此与铅笔具有相同金融风险的金融证券为政府所发行的公债，其报酬为无风险利率，因此δ＝r－α＝r。然而如果在标的物为交易性金融资产的状况下，若所有的股票供给完全为投资人所持有，并且假设股票不支付股利，则均衡的条件为αs＝α，或者说δ＝0，因为在均衡状况下，持有股票的机会成本αs必须等于其预期报酬α。

对于完美市场条件下的实物期权定价机制，可以假设存在一孪生交易证券（twin security）S（也就是对等风险的交易证券），S与θ具有相同的金融风险，并支付固定股利率（δ＝αs－α），则这个孪生交易证券必须满足（α＋δ）－r＝λσ，所以（α－λσ）＝r－δ。将其代入一般化定价偏微分方程（7－7）中，则在标的物为非交易证券的状况下，偏微分方程的形式变为：

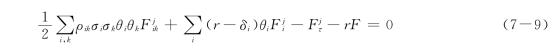
式（7－9）独立于投资人的风险偏好，因此无论融资标的物有无交易，都可以用风险中立的评价机制来做评价；在给定αs－δ＝α的条件下，可得α－λσ＝（αs－λσ）－δ＝r－δ；这等于是风险中立的评价，其中实质增长率α变成由对等风险中立漂移项（equivalent risk－neutral drift）αCE（αCE＝αs－λσ）所替代，通过预期增长率的调整，便得到了风险中立下的定价模式。对于拥有均衡报酬而不支付股利率的交易证券而言，αCE＝α；而那些不具有系统风险（λ＝0）的实质资产，如高科技研发融资方案，或勘探、开采矿产资源αCE＝α，若不存在股利率则αCE＝r；而对于具有股利率D的交易证券，αCE＝r－D；对于没有交易的资产而言，αCE＝α－λσ＝r－（D＋δ），则为其风险中立的增长率。

因此，实物期权基本上与金融期权的定价模式相似，即使标的物不是交易证券；Trigeorgis（1993）指出因为在资本预算上，人们的兴趣在于“融资方案的现金流量”在有交易的情况下的价值是多少。也就是说，其对于厂商市场价值的贡献度是多少。因此，如果存在一个与非交易证券具有相同金融风险的孪生证券，就可以用实物期权进行定价。

（三）多期复合式期权的融资方案评估

自从Geske（1977）提出复合式期权的公式解（closed－form solution）以来，复合式期权的概念已广泛地运用在财务模型上，Geske（1979）曾对复合式期权进行了定义：“许多机会本质上有先后序列的性质，只有在前一次机会获得执行，下一次机会才有获得履行的可能，这也就是复合式期权的性质，或者说是期权的期权。”

Kemna（1993）以二阶段复合式买权来评估创业（start－up）企业成长期权（growth option）的价值，然而以Kemna（1993）二阶段复合式买权来处理具有多个决策阶段的高科技创业融资方案似乎过于简化，不能反映序列投资中决策点的决策价值，进而失去使用复合式期权的意义。而Keeley，Punjabi and Turki（1996）的多期复合式买权，假设孪生证券的期望报酬为无风险利率，则又忽略了非交易性资产的特性。

Kemna（1993）以二阶段期货型复合式买权（call on call－on－future）模型，来评估公司成长期权的价值，他将公司的发展分为两个阶段，分别是：先期投资（pioneer venture）与商业投资（commercial venture）。先期的投资如设立公司前的准备费用、基础建设费用等，商业投资如公司核心设备的支出、营销推广费用等。通常商业投资要远远高于先期投资，而先期投资却是取得商业投资的必要步骤；商业投资所获得的价值要证明先期投资是值得支出的，两者互为因果，以期权的定义来看这个投资性质，这就是一个标准的复合期权的概念。若假设F为商业投资现金流入的现值，K为商业投资现金流出的现值，K＊为先期投资现金流出现值，r为无风险利率，τ为第二个期权的到期日，τ＊为第一个期权的到期日，Φn为一n元累积正态分布，则这一符合期权的评估公式可表达为：

推导得出。

然而Kemna的处理却有值得讨论的地方。公司的发展可分为两个阶段，但其中投资支出的决策点却并不只有两个，然而Kemna的处理却是分别将两期中多笔的现金支出流量利用现金流量折现方法折现到两决策点上，再利用复合式期权进行创业融资方案的评估，然而这样的处理将不能反映序列投资中决策点的决策价值，进而失去使用复合式期权的意义。

此外，KPT（1996）表示创业融资方案具有多期序列投资的特性，风险投资公司从业者在每一个阶段进行前都会评估是否继续，若评估一个高科技创业融资方案的价值时将这一重要特性忽略，将无法正确评估融资方案的真实价值。因此KPT（1996）以三维树多期复合式买权为模型来展现风险投资公司多期融资与高风险的事业特性，他们的模型沿用金融期权的评价机制进行融资方案的评估，忽略了创业融资的融资标的物为非交易性资产的事实，并利用方格树模型（lattice model）回避了复合式期权公式求解的困难。

由以上的文献得知，一个完整的创业投资评价模型，必须将近似股利率这样的参数纳入考虑，以修正融资标的为非交易性资产对于评价机制所造成的差异，并且模型要能反映创业投资多期与高风险的特性，基于以上两点，这里将使用多期的复合式期权来描述创业投资多期分次融资的投资特性，并对将非交易性资产纳入期权理论后对评价机制带来的差异进行探讨。

创业事业阶段分为：种子期（seed）、创建期（start－up）、扩展期（expansion）及成熟期（growth－up）融资，于模型的设立上，这里假设风险投资公司决定由种子期（或称第一期，）开始给予融资，以至于到达成熟期的融资，最后（第五期）辅导融资标的公司的股票公开上市，标的公司由依靠风险投资公司融资到能自行融资（self－financing）为止，风险投资公司总共需要给予四次融资。因此，风险投资公司若采用或有请求式（contingent claim）的投资策略，则将拥有五个决策点，在每个决策点上，风险投资公司都有视情况判断是否应该继续给予融资标的公司下一阶段投资的权利。

为了简化分析，假设风险投资公司于最后一个阶段买下融资标的公司所有公开上市的股份，取得公司经营权，进而享有整个公司公开上市的总市场价值（这个假设的用意在于避免产生设定公司股权比例的问题，而将焦点集中在多重决策点所带来的决策弹性价值与影响融资方案价值的因素，即敏感度分析）。

基本上，此问题可视为一种多期的实物期权，使用Geske（1977）复合式期权的概念来描述风险投资公司序列的投资行为，从而根据高科技创业企业创业的不同阶段来做分类，建立多期复合式期权模型，来评估高科技创业企业融资方案的价值。

1．创业价值的合理性演化

假设V表示企业价值，Iti表示给予融资标的公司的融资额度，IT表示初次公开上市（IPO）的总值，αV表示企业价值的瞬间期望报酬，σV表示企业价值的瞬间波动，δ表示近似股利率，Zx表示变量x遵循Wiener process，Cn代表n维的期权，而hij与kij代表第i期对融资方案做评价中累积正态分布的第j个变量。在企业价值演化过程遵循几何布朗运动的条件下，其表达式为：

而给予融资标的公司的融资额度It1、It2、It4和It5为契约内容事前订立的金额，并且初次公开上市的总额It5，这里也假设为事前已知。式中的最后一项dZV为Wiener增量（Wiener increment），服从正态分布，其平均数为0，标准差，所描述的是企业价值演化过程中不确定的部分，因此几何布朗运动下的公司未来价值总是不确定的，并且服从对数正态分布，其中在第T期企业价值的期望值E（VT）＝V0eα（T－t），变量－1］。

本模型采用几何布朗运动来描述风险投资公司所投资的高科技创业企业价值的演化有其合理性：几何布朗运动主要的特性为变量会随时间区段的增加而变大，由于创业融资方案本身蕴涵高度的风险，随着融资方案时间的增加，不确定性也会大幅上扬。

2．复合式期权的构建

风险投资公司对融资标的公司的第四期融资，也就是公开上市之前，可视为拥有一简单期权；而于第五阶段当风险投资公司买下初次公开上市的总值后，则可拥有整个公司的市场价值，这个简单期权的形式可表示为Max（Vt5－It5，0）；当公司的价值超过初次公开上市的总值时，则风险投资公司会去执行这个期权，此时这个期权的价值可表示为Ct5，t4，其中第一个下标代表期权的到期日，第二个下标代表对期权做评价的时段。

风险投资公司于公开上市的前一阶段会根据Ct5，t4的价值去判断是否应该继续给予融资标的公司融资，当Ct5，t4－It4＞0时，代表未来标的公司上市的期权价值会高于现在的资金投入，因此风险投资公司会进行融资方案，而当Ct5，t4－It4≤0时，则放弃融资方案，以公式表示为Max（Ct5，t4－It4，0）。

依此类推，于第三期风险投资公司会根据Ct4，t3的价值与融资额度It3相比，决定融资方案是否应该继续。较为特别的是此时风险投资公司所拥有的买权Ct4，t3为复合式买权的形式，Geske（1979）将这个概念用数学函数表示如下：

C2（V，t）＝f（C1，t）＝f（g（V，t），t）

C2复合式买权的标的物为简单期权C2，其最终的价值来自公司上市后的市场价值，这样才形成所谓的复合式期权。

3．评估公式的构建

由于期权的价值是来自于公开上市后公司的总市值，并且以时间为函数，假设C2（V，t）的价值演化过程遵循几何布朗运动，则：

dC2的形式表示为伊藤引理（Ito’s Lemma）为：

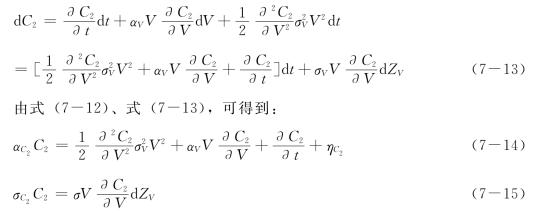
当且仅当ρVC2＝1时，

文献探讨中曾提到，在实物期权的研究范畴中，融资标的多为非交易性资产，需要构建合理的避险组合以符合风险中立的评价机制。在此将引用Merton （1973）的三证券投资组合（three securities portfolio）方法导出定价方程。

这个投资组合包含企业价值、期权价值、无风险证券三个要素，其中第一项的企业价值因为公司尚未正式上市，故视为非交易资产，三项资产的投资金额分别为n1、n2、n3，而投资组合的总额设为零，即n1＋n2－n3＝0。令d∏为这个投资组合的瞬间动量，则：

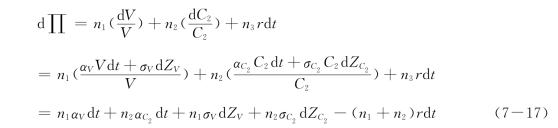
当ρVC2＝1时，式（7－17）可转化为：

若策略选择为，使得dZV＝0，这样一来此投资组合的瞬间报酬则成为非随机性变量，此外由于投资组合d∏的净值为零，必须避免套利空间的存在，也就是此投资组合的瞬间预期报酬应该为零，则此无风险、无套利的状况可表示为：

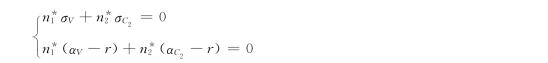
若存在非零解，则n＊j≠0，并且：

由式（7－14）、式（7－15）可得：

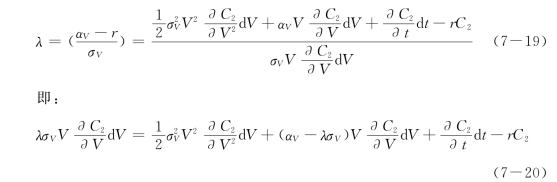
如同在文献探讨中所提及的，在完美市场下，假设存在一孪生交易证券S其与标的企业价值V具有相同的金融风险，拥有均衡的报酬αs（αs＝r＋λmρVm σV），与公司期望报酬间的短差为δ（δ＝αs－αV＝r＋λmρVmσV－αV），则这个孪生交易证券必须满足αV＋δ－r＝λσV，所以αV－λσV＝r－δ。将其代入式（7－20）中，可得在标的物为非交易性资产下的偏微分定价方程，其形式为：

式（7－21）所描述的便是复合期权C2的抛物线偏微分方程，任何以高科技创业企业价值及时间为函数的期权价值都满足上式。这个期权的到期日为t4，也就是这个期权的限制条件之一。于到期日t4时段上，期权Ct4，t3（或说C2）的价值为，当期权的价值低于某一临界值时，期权的价值为0，若超出，则期权的价值为与融资额度It4间的差额。但需要注意的是，在式（7－21）中真正决定C2价值的并非C1，而是厂商的总市值V。其中C1＝C1（V，t），其伊藤引理形式为：

经过以上的推导，可以得到C1的抛物线偏微分方程如下：

4．创业融资复合期权模型

在最初模型的设定上，假设当风险投资公司买下高科技创业公司初次公开上市的总值后，即可拥有整个公司的市场价值，而判断是否该执行这个权利的公式为Max（Vt5－It5，0），它同时也是式（7－23）的初始条件，这样可以求得简单期权的公式解如下：

式（7－24）中：

与式（7－21）相比较，求解式（7－23）相对困难了许多，因为式（7－23）的初始条件恰好是式（7－21）的解，即式（7－24）。在C2的到期日时段上，期权执行与否的关键在于Ct5，t4的价值是否超过执行价格It4，而Ct5，t4的价值是通过Max（Vt5－It5，0）所计算出来的。于是可以得到一个临界的厂商市值，使得风险投资公司是否要执行这个期权没有任何差别，即，t5）－It4＝0。这样，任何低于的高科技创业企业市值，风险投资公司都不会去执行这个权利，而相对的当高科技创业企业的市值高于，则会去执行这个权利。

于是可依照Geske（1979a）的方式求得Ct4，t3复合期权公式如下：

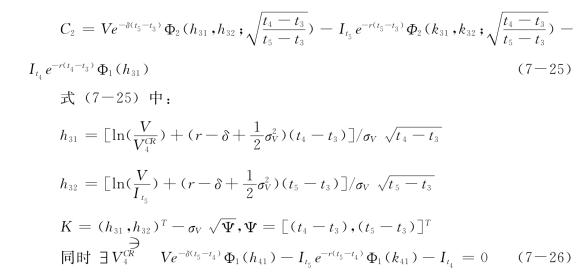
利用式（7－23）到式（7－26）的推导原理，同理继续推导求解，分别可求出创建期及种子期的三维、四维复合式期权的公式解，一直延伸到第n期，其一般公式表示如下：

式（7－27）中，n代表投资创业融资方案的期数，在本模型的设定下n＝5，在第一期（i＝1＝t1）评估融资方案的价值时，可用C4（即C5－1）表示。

在复合式期权的求解上会遇到两个有一定求解困难的问题，第一个为非线性公式求解：即在每一期中，期权的持有者会得出标的物价值的临界值VCR，使得风险投资公司是否要执行这个期权没有差异。第二个问题，为多元正态积分Φn（·）的求解，这里，将利用Drezner（1992）的已有成果，并参照Steen，Byrneand Gelbard（1969）以w（x）＝exp（－x2）作为权重函数的数值表，再利用高斯积分，来求解多元正态积分。

三、高科技创业企业股权融资契约

（一）高科技创业企业融资中的代理问题

高科技创业企业融资中的代理问题，主要分成两类：一类是高科技创业企业资金来源的问题，主要是指高科技创业企业与外部投资人存在信息不对称的问题，外部投资人往往对于高科技创业企业的经营行为、风险的偏好等，都有不同的要求而导致代理问题的发生。另一类是高科技创业企业融资资金用途的问题，主要是指投资者与创业家各有不同的专长，例如，风险投资公司擅长于管理、咨询、行销等，创业家则对技术的创新、产品的价值等更为了解，因而导致风险投资公司与创业家之间的代理问题发生。

Sahlman（1990）在对风险投资公司与创业家契约处理的研究中指出，风险投资公司借着阶段式的投资方式，保留放弃前景不被看好或更换经营团队的权利；风险投资公司与创业家共同享有公司的股权，使得风险投资公司与创业家的利益趋于一致，并激励创业家积极投入被投资的公司，减少与创业家之间的冲突；风险投资公司利用可转换特别股，享有股利、债权优于普通股及赎回条款，来保障风险投资公司的权益，减少代理问题。

Chua and Woodward（1993）利用净现值法（net present value approach）的方式，探讨风险投资公司与创业家的代理问题。风险投资公司与创业家的代理问题源自于预期的差异，因为创业家对公司的前景通常较风险投资公司乐观，两者对于公司未来的收益与价值有不一致的看法，而产生预期的差异。利用证券期权可以解决风险投资公司与创业家之间的代理问题。

Gompers（1995）以实证的方式，检测阶段性投资是否可以解决风险投资公司与创业家的代理问题。Gompers利用有形资产占全部资产的比例、市价对账面价值的比例、市场研发密度等三个衡量指针，衡量因信息不对称所导致的代理成本。被风险投资公司投资的公司为样本（共794个随机样本），其结论是当资产较不具有形性、市价对账面价值的比例增加、市场研发密度提高之下，则代理成本会增加。且风险投资公司若投资于高科技产业的公司与新创业成长阶段的公司，信息不对称的情况最严重，风险投资公司需运用监控机制与选择的功能，即以多期融资契约的方法，让风险投资公司拥有放弃继续融资的期权，降低信息不对称避免道德风险的发生。

Bergemann and Hege（1998）考虑一个动态的代理模型，创业融资方案的价值在期初时是不确定的，且更多的信息需要通过创业融资方案的实施才能获得。因此，资金的分配与学习的过程会受限于道德风险的情况。最优化的契约是风险由风险投资公司与创业家共同分担，而代理成本将会导致无效率的创业融资方案，只有通过监控与管理权有可能被替代的选择，来改善契约的有效性。

有关解决风险投资公司产业的代理问题，有一系列的研究，例如，Trester（1998）、Lulfesmann（2000）、Bascha and Walz（2001）及Cornelli and Yosha（2003），以比较可转换证券（或可转换债权）、普通股及一般债权的差异，得到的结论类似，即可转换证券（或可转换债权）优于普通股及一般债权，并证明可转换股票（或可转换债权）可以解决信息不对称所引发的代理问题。这里，将普通股及可转换股票的特性，引进代理模型，发现可转换证券的设计机制的确优于普通股。

（二）高科技创业企业融资中的道德风险

道德风险是指无法观察的自利行为，而双方道德风险是指代理理论中的委托人与代理人都采取无法观察的对方自利行为。风险投资公司可协助公司的经营管理（例如创业家行销方案、人事管理等）；创业家对从事专业技术的研发则比风险投资公司有较明显的优势信息，信息的不对称是双边的，因此，风险投资公司产业存在双方道德风险的问题。

Repullo and Suarez（1999）认为创业家与风险投资公司双方无法观察的努力行为产生了双方道德风险的问题，双方道德风险问题将影响各阶段的融资问题。为了分析融资问题，Repullo与Suarez建立了“证券设计方法”模型，最优化的契约可以利用可转换特别股，使得期初投资者的风险降低，并且也可防止其股权被稀释化。

Casamatta（1999）针对创业家与风险投资公司两者都可能产生道德风险的情况下，首先假设创业家与风险投资公司的努力是可以完全观察的（即无道德风险），这一情况是最优化的状态；然而，若是两者的努力无法观察时（即为双方道德风险），对于双方道德风险问题的解决应从契约的诱因设计着手，诱因满足风险投资公司与创业家的期望报酬需至少大于或者等于其投资的金额。因此所享有的股份性质与其所投资的金额数量有关，对于投资少的一方（创业家或风险投资公司），所得到的股份是普通股；相对的，投资多的另一方，其股份是可转换债券或可转换优先股，并将此推导印证于实务上，如天使投资偏好投资小额投资，而得到的股份大部分是普通股；风险投资公司所投资的资金较天使投资多，而风险投资公司也偏好可转换债券。

Houben（2002）将双方逆向选择与双方道德风险的观念运用于风险投资公司产业。他认为风险投资业不仅因创业家与风险投资公司的专长不一而存在不对称的私有信息，此私有信息导致双方逆向选择与道德风险的问题。因此，Houben将公司的状态分成三种（好、坏与普通），创业融资方案的报酬与状态好坏有关，在坏的状态之下，创业融资方案不应该执行，因为报酬并不足以补偿投资所花的费用；在普通状态时，虽然创业融资方案可以执行但是所付出的努力是属于较低水平的；只有在良好状态之下，风险投资公司与创业家都付出高的努力水平，此结果与Schmidt（2003）相同。Houben的文章指出传统的财务契约形式（例如，标准的债权契约、普通股契约）无法使得风险投资公司与创业家将个人的信息诚实披露。只有可赎回特别股及可转换特别股才能诱使双方诚实披露彼此私有的信息，待逆向选择的问题解决之后，双方才能做出有效率的投资决策，为创业融资方案付出的努力水平也是有效率的，双方道德风险的问题才能解决。

Schmidt（2003）是在一个不完全契约架构之下，处理双方道德风险的问题，并证明可转换债券可以使得创业家及风险投资公司付出最优化的努力。他将自然的状态分成三种（好、坏与普通），创业融资方案的报酬与状态的好坏有关，并假设风险投资公司可以不需耗费成本，观察到创业家的努力，发现在双方具有道德风险时，利用可转换公债当作一个诱因机制，风险投资公司只有在它拥有可转换权利时才会投资。同时也发现只有当创业家工作充分努力时，风险投资公司才会将债权转换成股票，但是创业家只有在好的状态之下才会付出最优化的努力水平。并且也证实可以转换的债券优于一般标准债权契约，通过可转换的债券机制，使得风险投资公司与创业家的报酬相关，当创业家越努力，公司的价值越高，风险投资公司转换成股票成为股东的意愿也越高，则其投入的资金与努力也越高，因此，当自然状态良好时，可转换债券的机制可以解决双方道德风险问题。

Kanniainen和Keuschnigg（2003）是从创业家与风险投资公司都有道德风险的情况之下，探讨风险投资公司最优投资创业家的创业融资方案的数目数量。他们认为双方道德风险的诱因机制，不仅重视企业家的努力，同时也重视风险投资公司的投入水平。风险投资公司最佳的投资数目与代理问题的严重性相关，因为风险投资公司所投入的管理水平与投资的数目会有相抵（tradeoff）的作用，过多的投资方案会排挤风险投资公司对每一个创业融资方案所投入的努力。当风险投资公司投入过少的管理时，创业家会要求分享较多的利润，使得风险投资公司的利润减少。

Keuschnigg与Nielsen（2004）主要是以“创业家与风险投资公司都存在的道德风险”为基础，探讨资本利得课税将会减少创业家与风险投资公司的努力，也导致最佳的福利受到损失，而减税将可以激励创业家与风险投资公司投入较多的努力。基本上，Keuschnigg和Nielsen的文献是从租税与公共政策的角度，来探讨风险投资公司与创业家的活动的先驱。

（三）高科技创业企业股权融资的契约模型

由于我国目前的大部分创业投资机构都有强大的地方背景，因此很难与其他创投机构共同投资某一家高科技创业企业。这种现实情况导致了我国绝大部分高科技创业企业在同一时刻只有一个创业投资股东，即使是我国目前被誉为最成功的高科技创业企业——盛大网络，也是在与中华网的关系破裂两年以后，才引入软银的新风险投资公司资金。因此，这里，将根据我国的实际情况，着重讨论创业家拥有创新的技术，但缺乏资金，需要风险投资公司的资金援助的情况。此时，风险投资公司可以通过普通股契约，也可以通过可转债契约进行援助，但根据问卷数据与实地调研，我国绝大部分高科技创业企业生命期不长，一般不具备非担保性质的债务偿还能力，因此这里侧重于对普通股契约模型的探讨。

1．模型的描述

有一高科技创业家（entrepreneur，E），拥有一个可以潜在获利的投资计划，但是创业家缺乏资金。此计划需要一个期初的投资资金，而创业投资家（venture capitalist，VC，以下简称风险投资公司）可以提供这个资金，供创业家成立公司。风险投资公司与创业家（被投资的公司）之间的关系，Jain与Kini（1995）认为风险投资公司的角色是委托人，而创业家是经营风险投资公司所提供的资金，因此，创业家是代理人。这里，假设创业家与风险投资公司均只有一位，风险投资公司将其所拥有的资金投资于创业家的计划，风险投资公司与创业家都是风险中立者（Lulfesmann，2000；Houben，2002）。

将时间共分成两期（时段0至时段1为第一期，时段1至时段2为第二期），在时段0时，创业家吸引风险投资公司的资金来投资其计划，双方签订一个期初契约，契约有两种：一是采取普通股契约；二是可转换债权契约。期初时（时段0），创业家需要的资金的总额是L（L≥0），风险投资公司提供期初资金L之后，创业家开始从事其计划。创业融资方案的价值为X，时段1时，有两种不确定因素会影响时段2创业融资方案的价值，一是风险投资公司与创业家投入的努力水平，二是自然的状况θ（state of nature，例如，经济环境），是指最佳的自然状态。假设当0，也就是说自然状态不理想时，创业融资方案的价值为负；当时，，也就是说当自然状态良好时，创业融资方案的价值为正。这样，创业融资方案价值可以表示为：

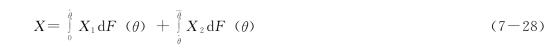
其中，F（θ）为自然状态的连续概率累积分布。时段2的创业融资方案价值会影响风险投资公司执行契约的方式。在时点0，若双方签订可转换债权契约，风险投资公司可以根据时点2所观察的创业融资方案价值，要求创业家偿还其资金或将其资金转换成股票，成为公司的股东，如表7．1所示。

表7.1　融资时间顺序表

风险投资公司除了提供资金之外，还可以协助创业家经营管理、生产规划、产品行销、融资与监控（Gormon and Sahlman，1989；Macmillian et al．，1989；Barry et al．，1990）。创业家对从事专业技术的研发则比风险投资公司较有优势，因此信息的不对称是双边的。另外，Chan et al．（1990）认为风险投资公司对于创业家的专业技术不如创业家了解，需要通过契约机制，规范彼此的权利与义务，以减少信息不对称的问题。

创业家向风险投资公司融资一笔资金L以实现其投资计划。创业家处理此资金的方式有两种，即与风险投资公司签订下列契约：一是普通股契约；二是可转换债权契约。根据我国的实际情况，这里主要讨论普通股契约。

创业家与风险投资公司在期初签订契约时，即约定双方都拥有公司的股份，未来公司的股权结构可以视实际情况及双方意愿而做调整。对于创业家向风险投资公司所借贷的资金，创业家不需还贷，而是让风险投资公司入主公司成为公司的股东，并让风险投资公司参与公司的发展规划与管理，因而普通股使得风险投资公司的报酬与公司的绩效有密切的关联性，风险投资公司可以分享公司的成长，这就是普通股契约。为不使模型过于复杂，在此假设创业家的薪资为0，创业家并没有资金投资，创业家对创业融资方案的付出，所得到的报酬为部分的股权（创业家所得的股权为技术股）。假设风险投资公司拥有φ比例的股份；创业家则拥有（1－φ）的股份，0＜φ＜1。

2．普通股契约模型(www.xing528.com)

正像Sahlman（1990）所言，创业家的薪资比在其他公司工作的薪资低，因此，认股权是一种激励。创业家所持有的股份，当公司发展壮大，价值提高时，认股权价值才会提高，而在转换之前也缺乏流动性，只有将其股份变现才会产生报酬。普通股的设计机制，可将风险投资公司与创业家的目标和利益连接在一起。

这里主要讨论在普通股契约的设计之下，创业家与风险投资公司双方分别在充分的信息及双方道德风险之下，双方对投资创业融资方案的付出水平存在差异。对于风险投资公司及创业家的目标函数的确定主要参考Lulfesmann （2000）的研究成果。

假设U为风险投资公司的效用函数，V为创业家的效用函数。风险投资公司于期初时，投入资金L，创业家并无资金，付出其技术，以取得公司股权的方式作为其报酬。普通股的契约协议内容为：高科技创业家因无资金投资，无需偿还风险投资公司所投资的资金，创业家的所得报酬是享有公司的股份。

风险投资公司追求其效用最大化，即：

其中，φ为风险投资公司拥有公司股份的比例，0＜φ＜1。m为风险投资公司参与公司管理所付出的努力，e代表创业家为取得所需技术所投入的努力，Ψ（m）为风险投资公司参与公司管理所耗费的成本，假设m、e是φ的外生变量（Houben，2002）。风险投资公司的效用最大化，即相当于风险投资公司的利润最大化，风险投资公司所得到的净利润等于其拥有投资创业融资方案的股份比例φ乘上创业融资方案的价值X后，扣除其付出的管理成本Ψ （m）。自然的状况θ如上所述，会影响创业融资方案的价值，所以是创业融资方案价值X的函数。

创业家追求其利润最大化，即：

其中，创业家所得到的收入扣除了其股份内的应得部分，并扣除创业家的成本C（e），即为创业家的净利润。

（1）信息的充分性。在Cooper和Ross（1985）一文中，所谓的充分信息是指双方在愿意合作的情况之下，追求双方的效用最大化总和或是最大总剩余。基于Cooper和Ross对充分信息的定义，双方采取合作行为，追求双方的效用最大化：

Max（U＋V）＝φX（φ，m，e，θ）－Ψ（m）＋（1－φ）X（φ，m，e，θ）－C（e）

⇒

式（7－31）对m进行偏微分，可得：

对e进行偏微分，可得：

其中，m＊将满足式（7－33），e＊将满足式（7－33）。因此，（7－22）与（7－33）是双方的最优合作解m＊与e＊。无论是出于哪种诱因，最优合作解要求创业融资方案的边际价值等于其边际成本，即Xm＝Ψm（m），Xe＝Ce（e）。在充分信息条件之下，双方没有人会有动机采取偏离这个最优合作解的行动。

（2）双方道德风险。双方道德风险是指双方只追求其独自的效用最大化（Cooper和Ross，1985），（m，e）的选择为非合作解。相对于充分信息的情况，若双方所采取的行动是非合作的，双方对于m与e的选择，只有在有特定诱因的情况下才能使双方采取适当的行为。

为建立双方道德风险模型，考虑两阶段的情况，第一阶段，双方先谈妥风险投资公司需投入的资金及双方各拥有的股份比例。进入第二阶段时，双方已知第一阶段的资金与股份比例，各根据已知的信息，选择其努力的水平。

当双方对于努力水平的选择是采取非合作的行为，此时需要计算反应函数的均衡解。已知φ，风险投资公司根据创业家的付出e的高低，选择自己投入的努力水平m，以追求其独自的效用最大化：

式（7－34）对m偏微分，令：

＾m将满足式（7－35）。

同理，创业家推测风险投资公司投入的努力水平m以决定自己的努力水平e，追求其效用最大化：

式（7－36）对e求偏微分，令：

＾e将满足式（7－37）。

在式（7－32）中，因为Xm（φ，m，e，θ）对m而言，是递增函数，明显大于式（7－35）的φXm（φ，m，e，θ）。Xe（φ，m，e，θ）。是e的递增函数，又，式（7－33）中的Xe（φ，m，e，θ）大于式（7－37）的（1－φ）Xe（φ，m，e，θ），因此＾m＜m＊；＾e＜e＊。也就是说，若风险投资公司与创业家签订普通股契约，0＜φ＜1，则＾m＜m＊；＾e＜e＊。简而言之，当0＜φ ＜1时，没有哪一方能够得到来自对方付出较多努力的利益，双方都有诱因想偷懒，因而在其各自的效用函数中，减少他们投入的努力水平。

Cooper与Ross（1985）一文的模型，主要是讨论一个简单的买卖契约，买卖双方各只有一位，买方所购买的产品质量不一定是好的，但是卖方在生产过程中，所付出的努力会影响产品质量；买方付出的努力（保管维护产品所付出的努力）数量也会影响产品质量。然而，双方所付出的努力是属于双方的私有信息，当双方处于充分信息时，卖方出售的产品质量比双方具有道德风险时佳；买方也付出较多的努力。因此，Cooper和Ross一文，其模型是建立在双方信息充分与双方具有道德风险的情况之下，比较双方所付出不同的努力水平与产品的质量。

正像上述的相关文献显示（Sahlman，1990；Gompers，1995；Neher，1999；Wang和Zhou，2002；Bigus，2002以及Cornelli和Yosha，2003），均只单方面考虑创业家或风险投资公司的道德风险问题。然而，Repullo和Suarez（1999）、Casamatta（1999）、Houben（2002）、Schmit（2003）、Kanni－ainen和Keuschnigg（2003）及Keuschnigg和Nielsen（2004）等人，认为若单方面考虑一方的道德风险，并不能解决真正存在的道德风险问题。因此，这里从双方道德风险方面着手，引用Cooper和Ross充分信息与双方道德风险的做法，应用于普通股契约，先了解在普通股契约之下，风险投资公司与创业家处于充分信息及双方道德风险的两种状态之下，其付出的努力状态各是什么样的。

Jesen和Meckling（1976）将代理关系定义为委托人委托代理人，并要求代理人需以委托人的利益为目标。但是若双方具有道德风险，只追求个人效用极大，则代理人并不会以委托人的最优利益为目标。因此，在各自追求其个人效用最大化之下，双方所付出的努力低于充分信息之下的水平。在普通股权的契约设计之下，只有双方都采取其最优化的努力水平，才能使公司的价值提高，创业家拥有的股权价值也会增加。

（四）融资契约中道德风险的解决

这里，根据Demski和Sappington的理论成果，尝试给出解决双方道德风险问题的方案如下：

风险投资公司于期初时，与高科技创业家签订契约，契约内容如下：创业融资方案所需的资金为L，风险投资公司投入资金L，风险投资公司可以决定是否让创业家拥有股权或是收回创业家股权。创业家若可以接受契约规范，创业家先付出技术与努力，风险投资公司在观察创业家的努力水平之后，也付出努力。创业家付出的努力程度，可以为风险投资公司带来有关未来创业融资方案期望价值的重要信息，风险投资公司因此可以决定是否让创业家拥有股权或是收回创业家股权。风险投资公司若是愿意让创业家拥有股权，创业家所得的报酬是与风险投资公司共同拥有公司的股份，风险投资公司拥有φ比例的股份；创业家则拥有（1－φ）比例的股份，创业家无须偿还风险投资公司所投入的资金。

风险投资公司所付出的努力水平，以m表示，m＊为风险投资公司能提供的最优努力水平；创业家的努力水平为e，创业家提供的最优努力水平为e＊。

在签约的最后阶段，若创业家同意签约，则表示创业家同意风险投资公司拥有收回创业家股份的权利，风险投资公司将其借款L的金额设定为是否收回创业家股权的阈值，当预期可分得的股权价值φX（φ，m，e，θ）≥L，风险投资公司才会让创业家继续拥有股份；当预期可分得的股权价值φX＜L时，风险投资公司收回创业家的股份，L为可支持创业融资方案执行的金额。假设k为风险投资公司愿意让创业家继续持有股权比例（1－φ）的概率，（1－k）为风险投资公司要求收回创业家股权比例（1－φ）的概率。则当φX≥L时，k ＝1，否则k＝0。

对于风险投资公司的效用函数U而言：

（1）k＝1，即φX≥L时，风险投资公司让创业家继续持有股权比例（1－φ），风险投资公司不收回创业家的股份，则风险投资公司拥有φ比例的股份，扣除所付出的努力成本Ψ（m），风险投资公司的效用U＝φX－Ψ （m）。

（2）k＝0，即φX＜L时，风险投资公司收回创业家的股份，风险投资公司拥有全部的股份，扣除付出的努力成本Ψ（m），风险投资公司的效用U＝X－Ψ（m）。

已知契约内容（L，φ），风险投资公司具有道德风险，风险投资公司只追求最大化个人的期望效用UE：

风险投资公司最优化的结果，是风险投资公司继续拥有部分的股权，即k＝1，而创业家也拥有部分股权，双方付出最优化的努力水平（m＊，e＊）。

对于高科技创业家的效用函数V而言：

（1）当风险投资公司不收回创业家的股份，创业家拥有（1－φ）比例的股份，扣除其付出的成本e，创业家的效用函数V＝（1－φ）X－C（e）。

（2）当风险投资公司收回创业家的股份之后，创业家的效用函数V＝－C （e）。

在创业家具有道德风险，选择自利的行为之下，最大化其期望效用VE：

VE＝Max｛k［（1－φ）X－C（e）］

在期初时，契约需能提供给创业家的期望效用VE≥V，V是创业家的保留效用。

风险投资公司最优化的结果，是风险投资公司继续拥有部分的股权，即k ＝1，双方付出最优化的努力水平（m＊，e＊）。风险投资公司可得φX（φ，m＊，e＊，θ）－Ψ（m＊），而创业家也拥有部分股权，创业家可得（1－φ）X （φ，m＊，e＊，θ）－C（e＊）。

以下证明k＝1时，风险投资公司与创业家都会选择（m＊，e＊）的努力水平，而无双方道德风险的发生。

假设创业家提供的努力水平为e＊，风险投资公司提供的努力为m，则风险投资公司的期望报酬是：

式（7－40）的第一项φX（φ，m＊，e＊，θ）－Ψ（m），是指当创业家付出最优化的努力水平，风险投资公司不收回创业家的股份，风险投资公司拥有φ比例的股份，扣除风险投资公司所付出的努力成本Ψ（m）之后的净利润；第二项X（φ，m，e，θ）－Ψ（m）则是创业家未付出最优化的努力水平，风险投资公司选择收回创业家的股份之后，扣除风险投资公司付出的努力成本所剩余的净利润。

风险投资公司最大的期望报酬是：

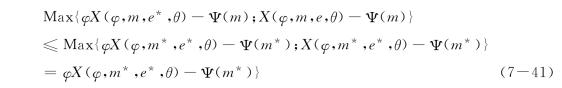
若创业家执行投资计划，未付出最优化的努力水平，风险投资公司要求直接收回创业家的股份时，风险投资公司所能得到的净利润φX（φ，m，e，θ）－Ψ（m），此净利润小于等于风险投资公司与创业家都为创业融资方案付出最优化的努力，风险投资公司能分得的价值φX（φ，m＊，e＊，θ）－Ψ （m＊），即X（φ，m，e，θ）－Ψ（m）≤φX（φ，m＊，e＊，θ）－Ψ（m＊）。

φX（φ，m＊，e＊，θ）－Ψ（m＊）为创业家提供e＊，风险投资公司让创业家拥有公司的部分股份，加上风险投资公司提供的最优努力水平m＊，在这种条件之下，风险投资公司所获得的净利润最大。

假设创业家将e的值设定为e≥e＊，则在契约设定的条件之下，风险投资公司可以确定下列情况：

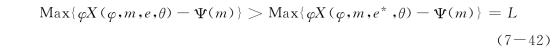
风险投资公司自己选择m的水平，使得φX（φ，m，e，θ）－Ψ（m）大于L，则风险投资公司让创业家继续保有股份，创业家可得：

创业家不会选择大于e＊的努力水平。

若创业家所选择的努力水平e＜e＊，则：

风险投资公司若继续让创业家持有股权，风险投资公司能分得的净利润φX（φ，m，e，θ）－Ψ（m）小于借款金额L，因此风险投资公司不愿意继续让创业家保有股份，收回创业家的股份，创业家未拥有公司的股份，则创业家所得为－C（e），创业家所能得到的利益如下：

V（φ，m，e，θ）＝－C（e）＜（1－φ）X（φ，m，e＊，θ）－C（e＊），e＜e＊（7－45）

创业家若无法持有公司的股份，其净利润为负值，创业家不会选择小于e＊的努力水平。

以上分析显示，一方面创业家付出e，当e≥e＊，创业家的净利润会小于其保留效用；当e＜e＊，创业家所得的净利润为负值。因此，创业家会选择付出e＊；另一方面，风险投资公司于观察创业家付出的努力水平之后，风险投资公司也选择付出有效率的努力水平，因此最优解的结果，风险投资公司与创业家双方选择有效率的努力水平，风险投资公司不收回创业家的股权，创业家享有（1－φ）的股权比例，风险投资公司享有φ比例的股权，在最优解的情况之下，风险投资公司投入的成本L等于其可得的净利润φX（φ， m＊，e＊，θ）－Ψ（m＊）。因此，综合上述推论，创业家会选择投入e＊以保有股份，而风险投资公司也投入m＊，双方道德风险的问题因而得以解决。

四、高科技创业企业创业融资

（一）高科技创业企业金融啄序理论

高科技产业自1970年以来，一直都是各国经济发展的重要产业。高科技产业结合了科技和工业力量，同时创造了大量的就业机会，因而世界各国与地区不但视高科技发展为地区发展的重要经济动力，更认为高科技产业可以促进较落后地区的均衡发展。而高科技创业企业已经成为各国高科技产业发展的重要推进力量，微软、戴尔、雅虎、EBAY、INTEL等耳熟能详的国际大型高科技创业企业的创业史，更加证明了高科技创业企业的诞生是未来生产力的重要影响因素。但由于高科技创业企业的经营基础比大企业薄弱，容易受经济环境变化的影响，加上高科技创业企业取得各类生产要素存在相对的困难，使其在创业初始阶段的经营环境更为不利。高科技创业企业在获取营运资金方面具有相当困难已是众所周知的现象。产生这种现象的原因主要是高科技创业企业很难向金融机构借得资金，而不得不借助其他融资渠道。

高科技创业企业之所以成功，除了具有技术、生产、营销、人力资源等方面的原因外，财务策略更是一项重要因素，企业在每个成长阶段都会面临不同的财务问题，企业是否能够生存与发展，依赖于资金的筹措是否适当及资金的运用是否有效。一方面，一个企业若能以比同行业较低的成本取得资金，则该企业必定有比同业较佳的竞争力；另一方面，企业若在任何经营阶段都能取得足够的资金，以应对资金支出的需求，则该企业也必定能够更长久地经营下去。

Donaldson（1961）研究美国公司的融资状况时发现在面对某一个有利的投资计划时，其融资行为存在着层级现象（Financing Hierarchy），即公司管理层偏好以公司内部资金作为优先的融资方式，除非遇到不可避免的资金需求暴增，否则公司不愿意使用外部资金作为融资来源。若公司必须向外部融资，公司也会尽量避免发行新股。

Myers和Majluf（1984），以信息不对称的观点来看待融资结构，系统地分析了Donaldson所发现的在美国企业之中普遍存在的融资层级现象，并提出了金融啄序理论来进行解释。其主要观点为，管理者基于追求现有股东财富最大化的原则，当管理者拥有的信息对现有股东有利时，即使放弃有利的投资机会，也会尽量避免使用外部资金。因此外部投资者为了了解管理者的意图，可以将企业的融资决策看成一种信号，若企业发行债券，外部投资者将视其为企业价值被市场低估的信号；若发行新股，外部投资者将视其为企业价值被市场高估的信号，因此信息不对称影响投资者所愿意支付的价格，也影响企业的融资决策。也就是说企业将优先使用内部资金，若内部资金不足时，将优先考虑使用无风险负债，其次考虑风险性负债，最后为权益证券。

Myers和Majluf之所以把融资的优先级排列为内部权益、债券、外部权益，并不全是考虑到资金成本因素，而是同时考虑到了企业内部管理者和外部资金提供者存在信息不对称的情况。通俗地讲，企业在进行融资时，首选使用内部资金是为了避免外部权益的股本介入而分散股权，同时也考虑到其不像外部股权或债务融资需要成本。但由于企业具有特定的目标股利政策，当有较佳的投资机会来临时，管理者希望在避免影响目标股利政策的前提下，才会使用外部资金。同样，企业使用直接举债来作为融资方式也是为了避免股权分散，且举债成本比发行外部权益低，另外的因素就是信息不对称和信号发射假说，即上文所说的进行举债对投资人而言是有利的消息，因为管理当局不会发行价值被低估的证券。而最后才考虑发行外部权益证券是因为其具有分散股权的特征且发行成本最高，同时还对投资人传递了市场高估企业价值的信息。所以由于上述几点原因，使得企业管理者在进行融资决策时，遵行金融啄序理论。

Myers与Majluf指出在完美市场上，所有的参与者拥有完整而相同的信息。然而完美市场事实上并不存在，事实上市场中存在很多信息不对称的现象。Narayanan（1988）通过理论推导发现：在使用外部融资时，获利程度高的企业会使用举债方式融资，并将绩效较差的企业逐出市场。因而市场中的剩余企业平均质量将会提高，所以获利较佳的企业喜欢举债。此外，Smith （1984）从破产角度说明，当企业有清偿能力时，对负债的高估不会超过企业的产出，而股价高估在任何情况下则均有利可图，所以企业喜欢高估股价而非高估负债，也因此，发行新股可能隐含企业获利能力变差或股价被高估的信息。在信息不对称下，Clarke与Wilson等人（1988）也指出，假如证券价格高于管理者的估计值时，企业会发行证券。在此情况之下，理性的投资者将修正其估计值。当信息差异越大，修正的幅度越大，发行新股所造成的价格下跌幅度也越激烈。

对于以上种种信息不对称的问题，Brennan ＆Kraus（1987）建议以最差的融资方式（Worst－case financing）来解决。假如企业认为投资者将以最低的价格评估企业的价值，则企业将被诱以最差的融资方式来符合投资人的评价；在此情况下，股价将不致低于完全信息下的融资价格。所以，如果投资项目的净现值为正数，则会接受此方案。Narayanan（1988）则认为如果企业保留足够的内部资金以满足大多数的资金需求，则可避免信息不对称所造成的成本。然而，当企业的内部资金不足，必须向外融资时，以上学者均认为举债融资较发行新股为佳。

在代理问题上，Jensen与Smith（1985）认为在企业组织中经常因管理人与代理人的利益冲突而产生代理问题。根据冲突群体，可将代理成本分成负债代理成本与权益代理成本。负债代理成本主要来源于股东与债权人在股利支付、求偿权稀释、产权替代、有利投资机会的放弃四方面的冲突；而权益代理成本则主要来源于所有权与控制权分离时，管理者无法分享所创造的财富或过度的特权消费所产生的成本以及管理者与股东所承担的风险压力不同所产生的冲突。

对于代理问题的解决，Haugen ＆Senbet（1987）认为无法依赖市场机能完全解决，必须依靠各种复杂的契约，他们建议以激励制度、监督控制及财务契约等方式解决种种代理问题。但这样必将增加设计复杂契约、制度等的代理成本，也就是说，只要是向外融资都会产生代理成本，而以内部资金融资资金需求则无此成本。因此，企业融资时的金融啄序将以内部资金为优先。由上述西方学者的研究可知，从信息不对称和代理成本理论两方面都支持金融啄序理论。

（二）我国高科技创业企业的金融啄序

1．金融啄序理论的实证研究

Baskin（1989）以1960～1972年财富500强企业中的378家企业为样本来研究金融啄序理论是否成立。根据静态最优融资结构的理论，资产负债比率和税前资产报酬率成正相关，获利愈高的企业，就有愈多的收入，则可能受限制于较高的边际税率，而破产的风险也越低。因此，获利愈高的企业，在静态的最优融资结构下，应该维持较高的负债比率。Baskin的实证结果显示企业的获利能力和负债比率呈负相关。因此，证明了金融啄序理论成立，即获利高的企业有足够的盈余来满足融资的需求，所以降低了对负债的需求，使得负债水平较低，由此实证结果也显示，静态的最优融资结构理论不成立。

Pinegar与Wilbricht（1989）为了解企业在选择融资结构决策时的观点，向1986年财富500强企业发出问卷，得到有效问卷为176份，其问卷调查的主要研究结果如下：

（1）在有效问卷中，68．8%的企业在选择融资决策时，以内部资金为优先，其次为直接负债及可转股负债，最后才考虑以发行新股的方式来融资。这个结果符合Myers与Majluf所提出的金融啄序理论。

（2）企业在进行融资决策时，所考虑的主要因素为：①投资项目的现金流量。②避免稀释当前股东的权利。③投资项目的风险。由于其中①、③项都与投资项目有关，所以投资决策及融资决策应是同时决定的，而并非传统的融资结构理论——MM理论所认为的投资决策与融资决策无关。

（3）许多企业认为市场并不具有效率性，因为企业的股价被市场正确定价的时间长短具有很大的波动性，因而市场的效率性对融资决策并没有太大的影响，也不会通过调整融资结构来传达企业价值的信息。Pinegar与Wilbricht对财富500强企业的问卷研究结果也符合金融啄序理论。

由于金融啄序理论建立在信息不对称的基础上，并且很多研究表明，美国的场外交易市场（Over－The－Counter，OTC）中的企业因为规模较小，无形资产占总资产的份额较高，因此信息不对称的程度比一般上市企业更强，于是Hittle，Haddad与Gitman（1992）以OTC企业为样本，验证OTC企业的融资行为是否符合金融啄序理论。他们发现，若以企业的市盈率作为信息不对称的指针，与大型企业相比较，这一比率的平均值及标准差都大于财富500强企业，也就是说OTC企业的信息不对称程度比财富500强企业更高。他们得到的主要研究结果为：

（1）OTC企业比财富500强企业更遵从金融啄序理论。

（2）OTC企业认为其自身的证券被市场正确定价的时间很短。

（3）企业投资及融资决策具有相关性。

2．融资总体情况的问卷调查

由前文西方学者对大型企业（财富500强）与中型企业（美国场外交易市场中的企业）的研究都表明，融资行为中的金融啄序现象实际存在，并且他们的研究表明信息不对称的程度越高，企业的融资行为越符合金融啄序理论。

我国证券市场中的大型企业（如中国石化、中国联通、招商银行等）与高科技创业企业相比较，在公布季报或年报的时间段内，高科技创业企业的股价波动幅度明显高于大型企业。也就是说，对于市场中的投资者（企业的外部股权融资方）来说，对于大型企业季报、年报内容的预测准确度要大大高于高科技创业企业，而预测的准确度是与企业信息的公开性与完整性密切相关的，因而在我国的证券市场，高科技创业企业的信息不对称程度大大高于大型企业。

由于高科技创业企业（高科技创业企业）存在信息不对称状况，本研究通过对高科技创业企业进行问卷调查的方式来了解高科技创业企业的融资行为，与金融啄序理论相印证的理论前提是具备的。

我国高科技创业企业的寿命普遍较短，《中国经济时报》在1999年4月3日刊登的消息称：中国数以千万计的高科技创业企业平均寿命为3．5年，中国人民大学在2004年对中关村的人力资源规划研究中也发现，中关村的企业平均寿命只有3．9年。产生这种现象的原因，除了主要高科技创业者对营销、市场等方面的不熟悉之外，主要是对企业的资金需求与资金获取难度认识不足。因此为了尽量避免失败的创业案例对研究结果的影响，作者针对武汉、长沙、北京、深圳等城市的高新技术产业园区中成立至今超过4年的高科技创业企业，对其从创立初始起的各个阶段的融资行为进行问卷调查，并结合金融啄序理论对发展的各个阶段的融资方式进行印证，为创业者创立并发展企业提供参考。作者共发出159份问卷，回收有效问卷126份。

根据各高科技创业企业在问卷中的融资方式部分，依照其成立后的不同年限阶段融资工具的不同重要程度（即本研究统计中的权重）填入数字（0～10）的结果，进行加权平均计算，统计结果，如表7．2所示。

表7.2　高科技创业企业融资方式调查问卷结果统计

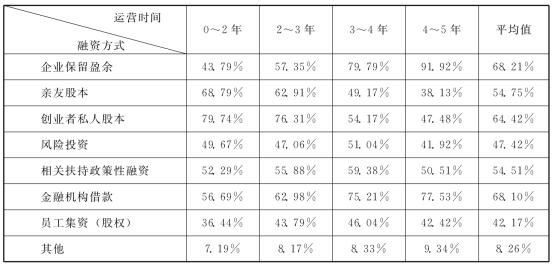
由表7．2可以看出，若根据中国高科技创业企业平均寿命4年左右的研究来划分企业成长的不同阶段，在创业0～2年，即初创至婴儿期内，创业者私人股本为最具重要性的融资方式，其次是亲友股本，而这两项都属于有利于集中企业控制权的融资方式。重要性排在第3位的是金融机构借款（直接债务融资），其后的融资方式才是风险投资股本（外部股权融资）。

在创业2～3年即少年期，情况与婴儿期基本类似，但金融机构借款重要性有所增加，成为第2重要的融资方式，说明高科技创业企业在发展到2～3年的阶段时，资金需求的满足仍需主要依赖创业者及其亲友，但由于企业已经运营超过2年时间，直接负债融资的能力在增长。

在创业3～4年即青年期，企业保留盈余成为非常重要的融资方式，说明青年期高科技创业企业的盈利能力进入高速增长的轨道，并已能用于满足企业的很多融资需求。同时，金融机构借款的重要性与前两期相比继续增加，间接说明企业的融资需求已不能被内部融资所满足，也表明高科技创业企业在青年期的直接负债能力有了质的改善，成为了与保留盈余几乎同样重要的融资方式。

在创业4～5年即开始进入壮年的时期，企业保留盈余已成为了绝对重要的融资方式，其重要性大大超过其他任何融资方式，说明企业的盈余大幅增加，能够满足大部分的企业融资需求。而金融机构借款在壮年期的重要性位于第2位，其重要性仅比青年期有微小的增加，说明在壮年期，高科技创业企业已经不再需要从金融机构借债来满足大幅超过内部融资能力的资金需求，从而扩张企业的产能。从此阶段开始，企业逐渐进入到平稳的成熟期，高科技创业企业的资金需求不再剧烈的变动。在这四个阶段里，风险投资与员工集资这两个融资方式的波动幅度并不是很大，且都不是最重要的融资方式，说明高科技创业企业为了避免分散控制权，并不会因为融资需求的增加（如青年期大幅扩张产能）而更重视这两种融资方式。同样，相关扶持政策性融资（如科研项目基金），在高科技创业企业成长的四个阶段里其作为一种融资方式的重要性也比较稳定。在企业成长的四个阶段内，高科技创业企业最重要的融资方式，如图7．2所示。

根据本研究问卷调查统计结果的平均值（见表7．2），综合来说，在企业融资方式的重要性排序中，企业保留盈余位于第1位，金融机构借款位于第2位，创业者私人股本位于第3位，亲友股本位于第4位，相关扶持政策性融资位于第5位，风险投资位于第6位并且其重要性在50%以下。此结果说明内部资金（包括内部股本投资与保留盈余）成为高科技创业企业毫无疑问的最重要的融资方式，其次为直接负债（金融机构借款），最后才是外部股权融资（如风险投资），与金融啄序理论是完全相符的。

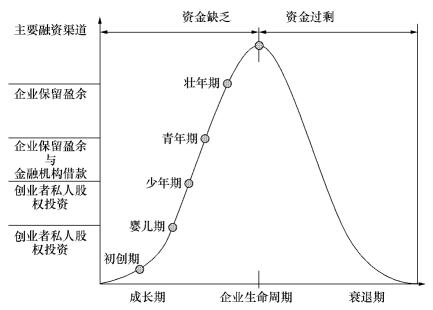
图7.2　高科技创业企业成长期内的主要融资方式

与企业生命周期相对应，创业资本可以采取如下不同形态，有种子资金、创立资金、运转资金、扩展资金及美化扩大资金。种子资金是当创业家提出其创业构想，同时希望再将此商品化时所需要的资金。这种投资的目的在于使创意构想商品化，其投资金额并不大，但风险特别高，有时人们也将其称为研发（R＆D）费用。一般来说，在企业创办前最需要此类资金。创立资金是在产品原型完成后，准备设厂进行生产时需要的资金。此时资金的需求量大，风险程度仍然较高。在企业创立阶段最需要的是这类资金。运转资金是产品虽然已经上市，但仍然没有达到盈亏平衡点。此时，需要相当数量的资金使企业运转。在这一阶段所需要的资金很大，但风险程度已经降低。通常，在企业成长的早期阶段，所需要的资金都属于此类资金。扩展资金是处于成长阶段的企业，已经达到盈亏平衡点，但为了再扩展，需要外界资金的支持。此类资金需要的数量很大，但风险相对较小。处于成长后期阶段的企业，最需要此类资金。美化资金是处于成熟阶段的企业，其发展的潜力已经充分展现，企业发展对资金的需求很大，非创业资本所能够提供，因此，需要安排上市。在股票上市前，为了增加企业的价值，可能需要一笔资金使企业得以美化，这类资金需要大小不一，但风险较低。这类资金包括：架桥融资、杠杆融资和再生融资。

信息不对称约束了创业企业的融资决策。如果信息不对称能够被消除，融资约束就会消失。专业化金融机构如创业投资机构能够解决信息不对称问题。创业投资家通过提供资本之前对企业的严格审查和投资之后对企业的严密监控，能够消除某些信息缺口，减少资本约束。许多理论研究探讨了创业投资家用以缓解创业企业和外部投资者之间的代理冲突的机制，这种机制包括监控和提供咨询（Comeli和Yosha，1997；Marx，1994；Hellmann，1998）、甄别机制（The Screening Mechanisms Employed；Chan，1983）、退出激励（Berglōf，1994）、适当的联合投资（Admati和Pleiferer，1994）或分阶段投资（Bergemann和Hege，1998）。

创业投资最常见的和突出的特征之一就是在各个阶段分配投资，资本分阶段注入是创业投资家所能采用的最有力的控制机制。分阶段注入资本使创业投资家能够收集信息，监控企业进程，并保持定期退出低质投资项目的选择权。创业企业的前景定期地被重新评估。单个轮次融资存续期越短，创业投资家对创业者进度的监控就越频繁，收集信息的要求就越大。分阶段资本投入对所有者／经理人是一种有效约束，减少了低劣决策所造成的潜在损失。因为风险资本融资谈判和组合的成本较大，所以资金分阶段来提供。

对投资者和创业者之间利益冲突的研究表明，创业资本投资的存续期和规模的影响因素：代理成本和监控成本，企业资产的性质，研发费用，市场价值／账面价值比率。创业投资者在潜在的代理成本和监控成本之间进行权衡，以决定对项目重新进行评估和提供资本的频率。当创业投资家认为与创业者的冲突有可能发生时，投资的存续期就会下降，再评估的频率就会上升。企业资产的性质也会对预期的代理成本和分阶段创业资本投资的结构有重要影响。有形资产越多，创业投资家就能通过清算形式取得越多的投资。这将会降低进行严密监控的必要性，增加投资的存续期限。研发费用水平高的行业会有更频繁的代理问题，创业投资家将缩短投资存续期限。最后，有相当一部分金融文献认为市场价值／账面价值比率高的企业更易受代理成本的影响，创业投资家将加强对这类企业的监控。

Paul A．Gompers在《风险投资周期》中通过一个包含794家创业企业的随机样本来检验影响创业资本分阶段投资的几个因素的有效性。检验结果证实了代理理论的预测。创业投资家把投资集中于那些信息不对称显著、监控会带来很大价值的早期阶段企业和高科技创业企业。创业投资家对企业的进程进行监督，一旦他们获得了任何有关未来回报的负面信息，那么就立即停止对该项目的再融资。公开上市的公司（平均来说，这些公司为创业投资家带来最高的回报）比其他公司（这些公司可能破产、被兼并或仍旧由私人持有）获得更多的总融资金额和融资轮次。处于早期阶段的公司每轮获得的融资较少。有形资产的增加可增加融资存续期和减少监督强度。随着未来投资机会（更高的市场价值－账面价值比率或R＆D密集性）在公司价值中的作用增加，公司将获得更多的再融资。这些结论表明创业投资家扮演着实施监控和产生信息的重要角色。

3．融资决策的因素分析

根据126份有效问卷的结果，接着分析高科技创业企业成立各阶段进行融资，其决策考虑因素的优先级别，以及各阶段是否具有差异性。研究项目分别用数字1～10表示，分别是：①产品销售稳定程度；②获利能力稳定程度；③长期资金成本；④未来投资及成长机会；⑤公司规模；⑥公司控制权的掌握；⑦偿债能力；⑧资产负债比；⑨附加价值的提供；⑩保留负债能力。该研究也是利用加权平均计算其重要性，根据重要性的五个等级分别赋予权重5～1，通过公式计算。分析结果如下：

1．成立初期融资决策考虑因素的分析

由表7．3以及图7．3可知，高科技创业企业成立初期融资决策考虑因素，前五个重要因素为：未来投资及成长机会、产品销售稳定程度、偿债能力、获利能力稳定程度以及公司控制权的掌握。

表7.3　成立初期融资决策考虑因素问卷结果

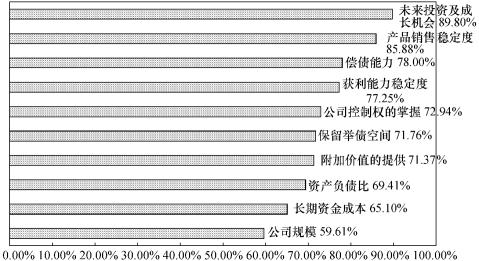
图7.3　成立初期融资决策考虑因素重要性排序

2．成立2～3年时融资决策考虑因素的分析

由表7．4以及图7．4可知，高科技创业企业成立2～3年时，其融资决策考虑前五个重要因素为：未来投资及成长机会、产品销售稳定程度、获利能力稳定程度、偿债能力、保留负债能力应对将来的投资机会。

表7.4　成立2～3年后融资决策考虑因素问卷结果

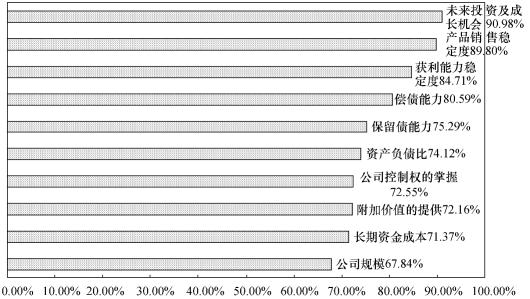
图7.4　成立2～3年后融资决策考虑因素重要性排序

3．成立4～5年时融资决策考虑因素的分析

由表7．5以及图7．5可知，高科技创业企业成立3～5年时，其融资决策考虑前五个重要因素为：产品销售稳定程度、未来投资及成长机会、获利能力稳定程度、偿债能力、维持适当资产负债比（资本结构）。

表7.5　成立4～5年后融资决策考虑因素问卷结果

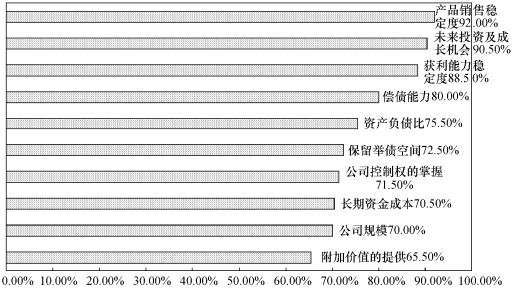
图7.5　成立4～5年后融资决策考虑因素重要性排序

4．成立5年后融资决策考虑因素的分析

由表7．6以及图7．6可知，高科技创业企业成立5年后，其融资决策考虑前五个重要因素为：未来投资及成长机会、获利能力稳定程度、产品销售稳定程度、偿债能力、维持适当资产负债比（资本结构）。

表7.6　成立5年后融资决策考虑因素问卷结果

图7.6　成立5年后融资决策考虑因素重要性排序

5．成立各阶段融资决策综合考虑因素

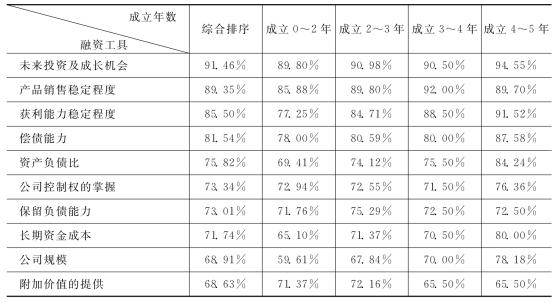
对以上问卷结果通过统计软件SPSS进行成立年数与融资工具之间的差异性分析，显示成立各阶段融资考虑因素具有91．3%的一致性。因此本文将各阶段重要性取其平均值，所得结果为整体重要性的排序，如表7．7所示。

整体而言，高科技创业企业在进行融资决策时，其考虑因素前五项为：未来投资及成长机会、产品销售稳定程度、获利能力稳定程度、偿债能力和维持适当资产负债比（资本结构）。而最不重要的因素前五项为：公司规模、融资机构附加价值的提供、长期资金成本、公司控制权的掌握、保留负债能力应对将来的投资机会。

表7.7　成立各阶段融资考虑因素的重要性排序