数学中的无理数发现与求近似值方法

趣　谈

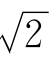，是人类最早发现的无理数。在古希腊，毕达格拉斯学派证明了：在如图所示的直线上，不存在对应于点P的有理数。

显然，距离OP等于边长为1的正方形的对角线。第一个无理数就这样脱颖而出。遗憾的是，因为新数的出现，动摇了毕氏学派“任何两个同类量都是可以通约的”信条，所以面对数学史上这一伟大发现，毕氏学派不是欢欣鼓舞，而是感到恐惧和困惑，采取了“不承认主义”。在万不得已时，毕达格拉斯找一个分数来代替它，先用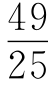近似地代替2，然后用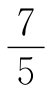代替。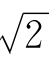

当然，真理的火焰是包不住的。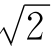，π，……等无限不循环小数——无理数，终于被人们所认识。然而，毕氏学派开创的用分数（一种简单的整数比）来近似地表示无理数，有很大的实用价值。

能不能求得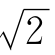的更好的分数近似值呢？

16世纪，意大利一位数学家邦别利首先利用连分数求。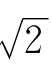

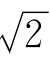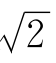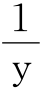因为＞1，所以不妨设＝1＋（1）

由此得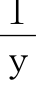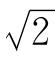＝－1，y＝1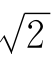＋所以y＝2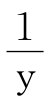＋（2）＝1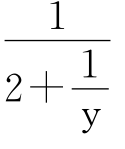＋（3）

再把（2）代入（3），得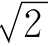＝1＋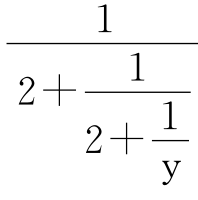

继续做下去，有

由此求出的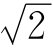的各种精确度的近似分数是：(https://www.xing528.com)

，，，，……

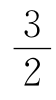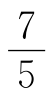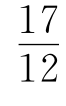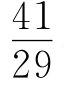公元3世纪，我国古代数学家刘徽使用的求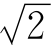的近似值的方法，也十分有趣。

他利用了这样一个近似公式：

容易看出，两边平方有a²＋r≈a²＋r＋。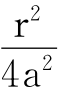

当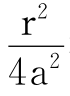很小时，两边近似相等。∵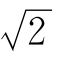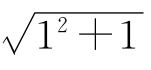＝，根据（Ⅱ），有

这样，只是把近似公式用了三次，就得到了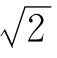的相当精确的近似值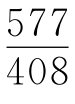：≈1．4142157。

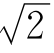和我们人类的生活关系密切，边长为1的正方形对角线长是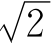，腰长为1的等腰直角三角形的底边是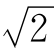，……你相信吗，我们阅读的各种书本的长与宽的比也是！

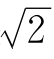在我们的猜测中，书本的长和宽之比应符合黄金分割，为什么是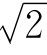呢？这是因为，书本是原张纸切开制成的。当把一张纸对分成两张时，我们总希望对分后的半张纸与原张纸相似。即

显然，继续将半张纸对分成两半，那么这半张纸与这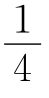张纸仍相似。

你看，多么有趣，而又出人意料！