数学中的趣味知识：质数理论与明珠

质数与明珠

自古以来，数学家对于整数的性质的研究一直十分重视，不过一直到18世纪末，各个研究成果只是散见于各个时代的算术著作中。我国古代也有许多数学家有这方面的论述，但记载比较零散，更没有系统成书。这时，高斯集前人之大成，写下了《算术探讨》这部杰出的著作，初步形成了一个统一的数学分支——数论。

数论在数学中的地位是独特的。高斯曾说：“数学是科学的皇后，数论是数学中的皇后。”从此，数学家们把数论中的那些悬而未决的难题称做皇后“皇冠”上的“明珠”，以激励人们去“摘取”。数论中皇冠上的明珠约有二三十个，但这些“明珠”的基础理论归根结底还是“质数理论”。

所谓质数，就是大于1的整数，除了它本身和1以外，再不能被其他正整数所整除的数。质数又叫素数。如2，3，5，7，11，……等等。不是质数的自然数叫做合数。

关于质数，有许多趣谈。(www.xing528.com)

公元前3世纪，数学家们就开始对质数进行研究，首先遇到的问题是：质数究竟有多少个？这个问题看起来简单，但得出结论并证明它却很不容易。最后是希腊数学家欧几里德首先证明了“质数有无穷多个”。

另一个问题也就随之产生了：给你一个很大的自然数，你怎样断定它是否质数呢？于是，数学家们又倾注了大量的心血，终于得出了一个定理：如果N是一个大于1的自然数，而所有不大于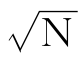的质数都不能整除N，那么N就是质数。由于定理的繁琐，有人就想到造一个“表”，尽可能多的将质数列在表上。由此产生了希腊数学家厄拉托塞的“筛法”。又有人想到，能否用一个公式来表达质数？一时间，众多的数学家在向这个难题冲击着，因为质数的分布太无规律性，各路兵马进展甚微，只得纷纷退却。

到17世纪，法国数学家费尔马（当时他是一名业余数学家）提出了一个公式：一切形如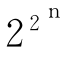＋1（n为自然数）的数是质数。然而好景不长，几十年后，这个结论就被欧拉推翻了，他证明了当n＝5时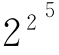，＋1＝641×6700417不是质数。接着他也给出了一个公式：x ²－x＋41（x为自然数），时间不长，就又被人们证明了当x＝41时不是质数。又过了若干年，法国著名数学家勒昂德提出了2x²＋29的式子，但当X＝29时，仍不是质数。到目前已经两千多年了，人们也只能用公式表达一部分质数，但用一个公式来表达所有质数这一愿望，仍在激励着一代又一代数学家们为之奋斗。