月亮宝石的价值及割开前后比较

月亮宝石的价值

你看过《月亮宝石》这本书吗？《月亮宝石》是十九世纪英国著名作家威廉·威尔基·柯林斯（1824－1889）的代表作，这本书被后世誉为“第一部英国侦探小说，也是最伟大的一部”。柯林斯也因此而被戴上“现代侦探小说的鼻祖”的桂冠。以写福尔摩斯探案小说闻名今世的柯南·道尔也在很大程度上受到他的影响。

这部小说是围绕着一颗价值连城的黄色的印度钻石而展开的。这颗宝石原来一直被镶嵌在一尊四只手的印度神——月亮神的前额上。

1799年，英国侵略者攻入印度圣城塞林加柏尔。官兵烧杀劫掠，无恶不作——就象他们当年在我国焚毁园明圆那样。英国侵略军军官亨卡什抢到这颗宝石后，把它带回英国。而印度爱国者不甘心国宝流落异邦，也跟踪来到英国，伺机夺回。亨卡什临死前把宝石送给侄女雷茜儿，但雷茜儿得到宝石的当晚就失窃了。于是探长登场大显身手。几经波折，扑朔迷离的案情终于真相大白。原来是以慈善家面目出现的雷茜儿的表哥艾伯怀特偷走了宝石。艾伯怀特一方面为了逃避印度爱国者的追索，另一方面也为了销赃方便，想把宝石带到阿姆斯特丹去割成几块，他认为宝石如被割成几块，不成完璧，印度爱国者就可能因为不能再镶嵌到月亮神像上而放弃追索，从而有利于他销赃。当然，宝石被割开，价值会大跌。但这笔飞来之财，对艾伯怀特来说也足够他挥霍的了。

宝石的价值，要看它的纯净度，还要看它的颜色。而在颜色纯度都一样的情况下，其价值与重量的平方成正比。这块宝石，据当时的宝石商，高利贷者鲁克的估价，至少价值30000英镑——这在当时已经可算是天文数字了。而且贪婪的鲁克也是为了杀价才这样压低估价的。就算这块宝石价值30000英镑吧，再假定这块宝石重G克拉（克拉是计算宝石的重量单位，1克＝5克拉），于是可知一粒重1克拉的这种宝石价值为30000英镑，不妨记K＝。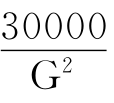

为方便计算，假定艾伯怀特准备把宝石割成重量为x克拉及（G－x）克拉的两块，于是割开后宝石价值y为：

y＝Kx²＋K（G－x）²＝2Kx²－2KGx＋KG²

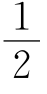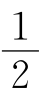　＝2K（x－G）²＋KG²。

显然，宝石的价值是x的二次函数，其中0＜x＜G，于是

｜x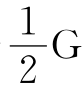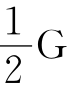－｜＜。所以2K（x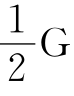－）²＜。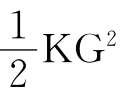

从而y＜KG²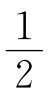＋KG²＝30000。

这就是说，割开后宝石价值一定受损失，且当宝石割成相等两块时受损失最大。此时的价值只有原价的一半。

这个问题用几何方法也可以说明。(www.xing528.com)

如图，取正方形ABCD中的线段AB表示月亮宝石的重量G，即AB＝G。

于是，月亮宝石的价值为KG²＝K·S_ABCD。

设宝石被割成重为x＝AM及G－x＝BM的两块。在正方形的各边上依次截取BN＝CR＝DP＝AM，则MNRP也是正方形。

两块宝石价值和y＝Kx²＋K（G－x）²＝K（AM²＋AP²）＝K·MP²＝K·S_MNRP。

显然S_MNRP＜S_ABCD，即割开后宝石的价值要受损失。

如果取正方形ABCD的四边中点E、F、G、H，则正方形EFGH的面积xK则表示宝石被割成相等两块时的价值，下面证明S_EFGH≤S_MNRP。

不妨设AH＞AP。作PS‖AB，交HE于S，且设HE与PM交于O，易证S△OEM＝S△OSP。

于是S_AMP＝S_AEOP＋S_OSP＝S_AESP＜S_AEH。

∴S_EFGH＝S_ABCD－4S_AEH＜S_ABCD－4S_AMP＝S_MNPR。

即当E、F、G、H为正方形ABCD的四边中点时，其面积取最小值，且S_EFGH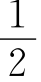＝S_ABCD。

当然，故事的结局是：正当化装成水手的艾伯怀特揣着宝石准备动身前往阿姆斯特丹时，探长们赶到了，但三位印度爱国者先到了一步，夺走了宝石并重新把宝石送回国镶嵌在月亮神的前额上去了。