巴霍姆围地：如何得到尽可能大的面积？

巴霍姆围地

俄国著名作家列夫·托尔斯泰在他的作品中写了这样一个故事：

巴霍姆想到巴什基尔人的草原上买两块地。他问卖地人价钱如何，卖地人说：“每天1000卢布。就是你如果愿出1000卢布，那么你从日出到日落走过的路所围成的地就都归你。不过，要是你在日落之前回不到原来出发的地方，你的钱就算白花了。”

巴霍姆觉得很合算，就付了1000卢布。第二天，太阳刚从地平线上一露面，他就连忙在大草原上奔跑起来。他先笔直往前跑了10千米，才朝左拐弯；接着又走了13千米，再向左拐弯；这样又走了2千米。这时，他发现太阳离地平线不远了，于是马上改变方向，笔直朝出发地点跑去。跑呀，跑呀，太阳已有一部分隐藏到地平线下去了，他还离开出发地点一段路呢。为了不使1000卢布白费，他用尽力气拼命地跑，总算在太阳全部消失之前赶回到出发地点。可是他向前一扑，口吐鲜血，再也站不起来了。

贪婪的巴霍姆为了能得到尽可能多的土地，结果累死了，弄得人财两空，这是他自作自受。但是，他却给我们留下了一个数学问题。下面我们来研究一下。

仔细阅读前面的故事把巴霍姆跑过的路程画出来就可以看出，形状是一个梯形。它的面积是（10＋2）×13÷2＝78（平方千米）。(www.xing528.com)

那么，巴霍姆的体力如果一天能跑40千米的话，他应该围怎样的矩形，才能得到尽可能大的面积？

学过二次函数的读者会得到正确的答案——边长为10千米的正方形围成的面积最大。

事实上，设矩形的边长为x千米，则相邻边长为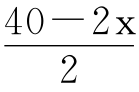千米。

∴矩形面积S＝（20－x）x＝－x²＋20x当x＝10时，S有最大值

S_最大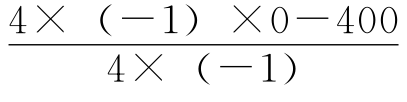＝＝100（平方千米）。