聪明发明者的奇思妙想：数学趣味解析

聪明的发明者

古时候有个国王很喜欢聪明的人，只要听说哪里有聪明之士，他便迅速召见，当面提出问题，以验证其聪明的程度，并当众给以重奖。有一天，他听说有人发明了一种漂亮的棋子和棋盘，便传令召见发明者。发明者把亲手制作的棋子与棋盘呈献给国王，并向国王详细讲解了这种棋的下法。国王听后十分高兴，决定当众给发明者以重奖。国王慷慨地问：“你希望得到什么奖赏？”发明者稍加思索，慢条斯理地说：“我是一个普通百姓，不敢接受国王的高贵奖赏，如果国王同意的话，只要送给我一些麦粒即可。”国王听后哈哈大笑，说：“你是一定要得到重赏的！麦粒有何用？这样吧，我可以用金银做成麦粒形状奖给你，你看如何？”发明者难为情地说：“尊敬的国王，您的好意我领了，您还是给我麦粒，回家后我好分给乡亲们。”国王见发明者执意要麦粒，便高兴地说：“你不但是位聪明人，还是一位不贪财的人。好吧！你要多少麦粒呢？”发明者指着国王面前放着的棋盘说：“请在第一棋盘格里放1粒麦子，第二格里放2粒，第三格里放4粒，如此类推，每增加一格，麦粒数便增加1倍，一直放满棋盘的64个格。陛下，您就把这些麦粒赏给我吧。”国王听罢，满口应允，于是便吩咐手下侍从，按发明者的要求去取麦粒。结果，所有仓库里的麦子都取来还远远不够，国王这才知道自己受骗上当，但国王的话乃金口玉言，又是当众说出，怎好反悔呢？无奈，国王问发明者：“到底需要多少麦粒才能按要求‘装满’你的棋盘呢？”发明者笑着说：“陛下，请让我慢慢算给你看！”

“这64个格中应分别放的麦粒数依次是1，2，2²，2³，……，2^{6 3}。”发明者说。

“是的，不错。”国王点点头。

“那么，64个格中共放的麦粒数应是N＝1＋2＋2²＋…＋2^{6 3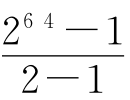}＝＝18446744073706551615对吗？”发明者问国王。

国王不太懂数学，便差人请来一位数学内行亲信在一旁“参谋”。发明者向这位“高参”简单介绍了问题的来龙去脉，他连连点头称是。国王急迫地问：“那么这些麦粒有多少包呢？”发明者继续计算着：“若按10000粒1斤，1000斤1包计算，这些麦粒大约有一万八千亿包。尊敬的国王陛下，您的粮仓内一共能有多少包呢？恐怕，连您的万贯家产全部卖掉换成麦粒，也装不满我的棋盘吧？！”发明者算完后对着众人哈哈大笑，但见国王早已是目瞪口呆、魂不附体了。

亲爱的读者朋友，以上当然只是一个传说、笑话而已。但是从中你可以初步体会到2，2²，2³，……2ⁿ，……这列按指数增长着的数的增长速度是多么大！实际上，聪明的发明者当时是怎样算出2^{6 4}－1这个数来的，我们暂不追究（大概是按2，4，8，16，32，64，128，……依次写出2^{6 4}，然后再减1吧）。现在我们可用对数工具简单估算一下这个数。lg 2^{6 4}＝64lg 2＝64×0．3010＝19．2640查反对数表知19．2640＝lg1．836×10^{1 9}。这是个20位数，与发明者算出来的数位数相同且首位数字与第二位数字也相同，可以说明这个数是如此之大了。

另外，上文中曾出现过一个算式：

1＋2＋2²＋……＋2^{6 3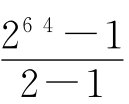}＝…………………………………………①

这是怎么得来的呢？下面介绍一下：(www.xing528.com)

∵（x－1）（1＋x＋x²＋x³＋……＋xⁿ）

＝（x＋x²＋x³＋x⁴＋……＋x^n＋1）

　　－（1＋x＋x²＋x³＋……＋xⁿ）

＝x＋x²＋x³＋x⁴＋……＋x^n＋1

　　－1－x－x²－x³－……－xⁿ

＝x^n＋1－1

∴1＋x＋x²＋x³＋……＋xⁿ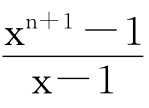＝，（x≠1）……………………②

这是一个经常用到的数学公式。在这公式中，设x＝2，n＝63，即得①式。